Vahid Keshavarzzadeh
Machine Learning in Heterogeneous Porous Materials
Feb 04, 2022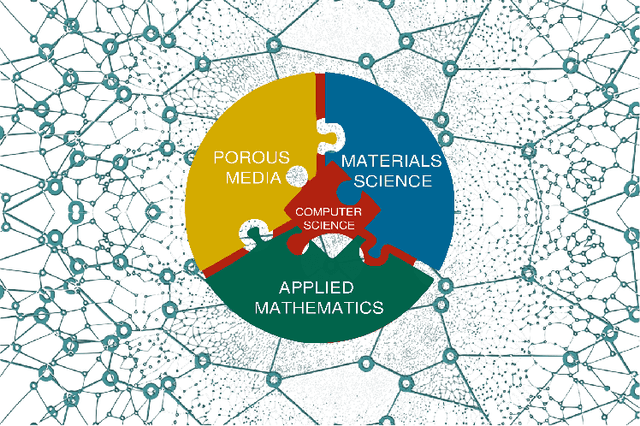

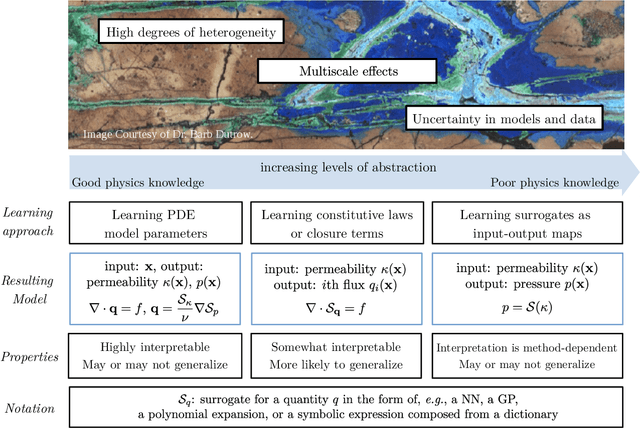
Abstract:The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.
Robust Topology Optimization Using Variational Autoencoders
Jul 19, 2021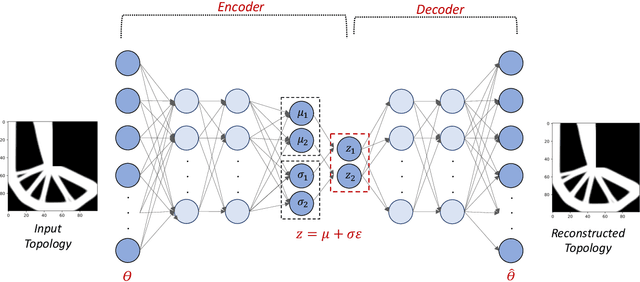
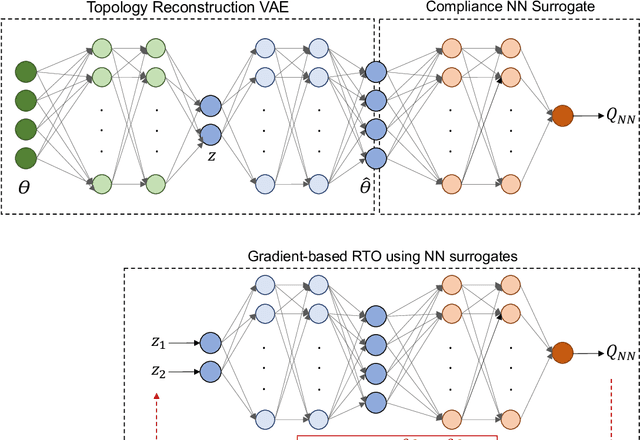
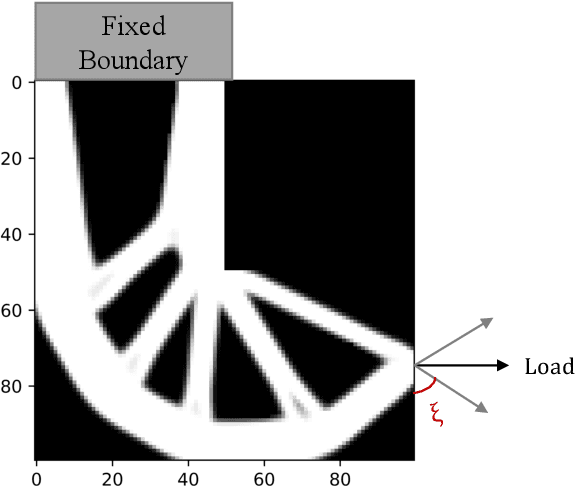
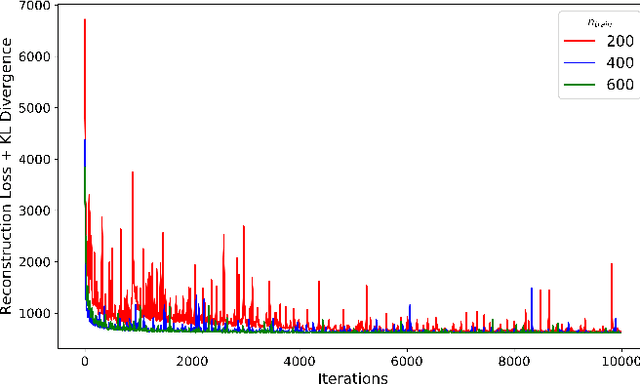
Abstract:Topology Optimization is the process of finding the optimal arrangement of materials within a design domain by minimizing a cost function, subject to some performance constraints. Robust topology optimization (RTO) also incorporates the effect of input uncertainties and produces a design with the best average performance of the structure while reducing the response sensitivity to input uncertainties. It is computationally expensive to carry out RTO using finite element and Monte Carlo sampling. In this work, we use neural network surrogates to enable a faster solution approach via surrogate-based optimization and build a Variational Autoencoder (VAE) to transform the the high dimensional design space into a low dimensional one. Furthermore, finite element solvers will be replaced by a neural network surrogate. Also, to further facilitate the design exploration, we limit our search to a subspace, which consists of designs that are solutions to deterministic topology optimization problems under different realizations of input uncertainties. With these neural network approximations, a gradient-based optimization approach is formed to minimize the predicted objective function over the low dimensional design subspace. We demonstrate the effectiveness of the proposed approach on two compliance minimization problems and show that VAE performs well on learning the features of the design from minimal training data, and that converting the design space into a low dimensional latent space makes the problem computationally efficient. The resulting gradient-based optimization algorithm produces optimal designs with lower robust compliances than those observed in the training set.
A bandit-learning approach to multifidelity approximation
Mar 29, 2021



Abstract:Multifidelity approximation is an important technique in scientific computation and simulation. In this paper, we introduce a bandit-learning approach for leveraging data of varying fidelities to achieve precise estimates of the parameters of interest. Under a linear model assumption, we formulate a multifidelity approximation as a modified stochastic bandit, and analyze the loss for a class of policies that uniformly explore each model before exploiting. Utilizing the estimated conditional mean-squared error, we propose a consistent algorithm, adaptive Explore-Then-Commit (AETC), and establish a corresponding trajectory-wise optimality result. These results are then extended to the case of vector-valued responses, where we demonstrate that the algorithm is efficient without the need to worry about estimating high-dimensional parameters. The main advantage of our approach is that we require neither hierarchical model structure nor \textit{a priori} knowledge of statistical information (e.g., correlations) about or between models. Instead, the AETC algorithm requires only knowledge of which model is a trusted high-fidelity model, along with (relative) computational cost estimates of querying each model. Numerical experiments are provided at the end to support our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge