Spatiotemporal k-means

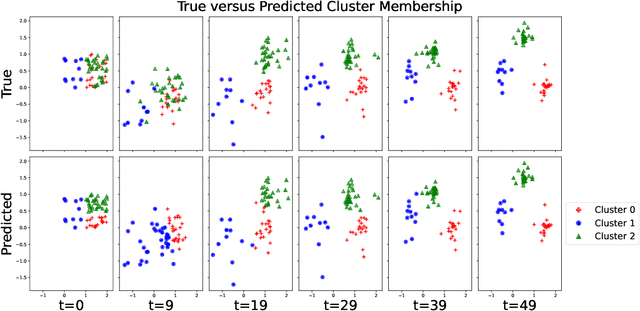
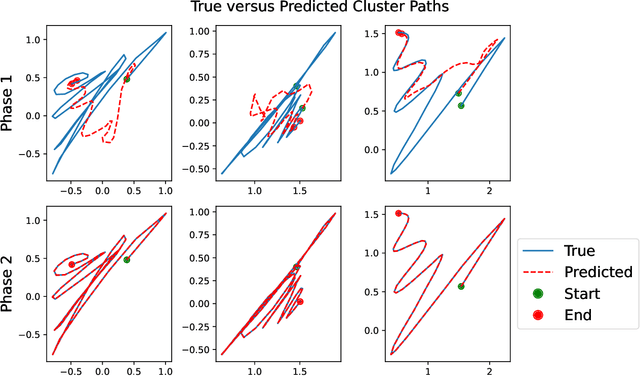
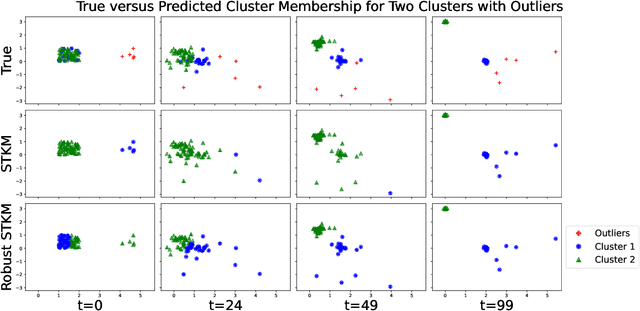
Spatiotemporal data is readily available due to emerging sensor and data acquisition technologies that track the positions of moving objects of interest. Spatiotemporal clustering addresses the need to efficiently discover patterns and trends in moving object behavior without human supervision. One application of interest is the discovery of moving clusters, where clusters have a static identity, but their location and content can change over time. We propose a two phase spatiotemporal clustering method called spatiotemporal k-means (STKM) that is able to analyze the multi-scale relationships within spatiotemporal data. Phase 1 of STKM frames the moving cluster problem as the minimization of an objective function unified over space and time. It outputs the short-term associations between objects and is uniquely able to track dynamic cluster centers with minimal parameter tuning and without post-processing. Phase 2 outputs the long-term associations and can be applied to any method that provides a cluster label for each object at every point in time. We evaluate STKM against baseline methods on a recently developed benchmark dataset and show that STKM outperforms existing methods, particularly in the low-data domain, with significant performance improvements demonstrated for common evaluation metrics on the moving cluster problem.

Machine Learning in Heterogeneous Porous Materials

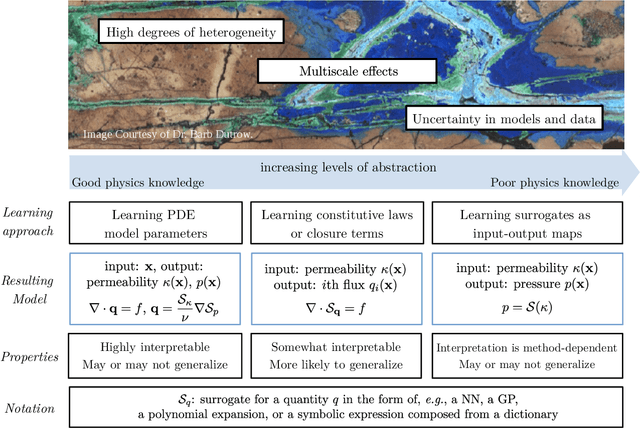
The "Workshop on Machine learning in heterogeneous porous materials" brought together international scientific communities of applied mathematics, porous media, and material sciences with experts in the areas of heterogeneous materials, machine learning (ML) and applied mathematics to identify how ML can advance materials research. Within the scope of ML and materials research, the goal of the workshop was to discuss the state-of-the-art in each community, promote crosstalk and accelerate multi-disciplinary collaborative research, and identify challenges and opportunities. As the end result, four topic areas were identified: ML in predicting materials properties, and discovery and design of novel materials, ML in porous and fractured media and time-dependent phenomena, Multi-scale modeling in heterogeneous porous materials via ML, and Discovery of materials constitutive laws and new governing equations. This workshop was part of the AmeriMech Symposium series sponsored by the National Academies of Sciences, Engineering and Medicine and the U.S. National Committee on Theoretical and Applied Mechanics.

Deeptime: a Python library for machine learning dynamical models from time series data

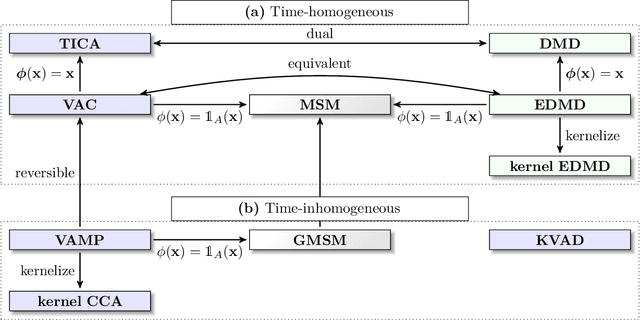
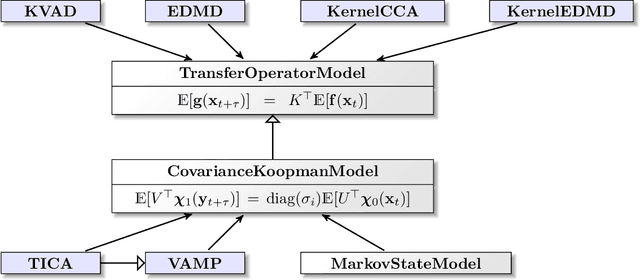
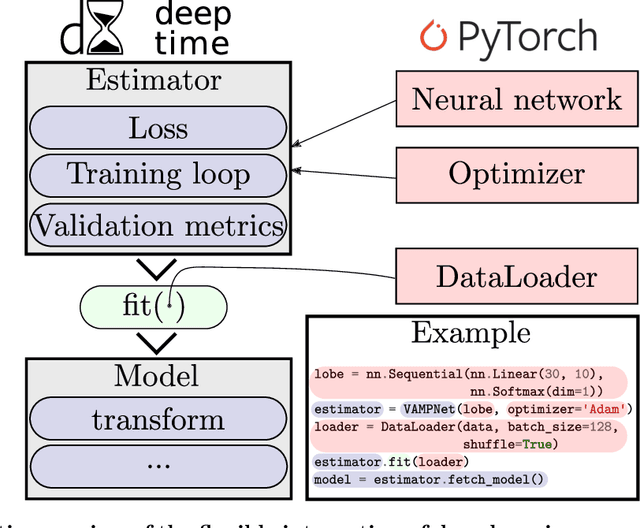
Generation and analysis of time-series data is relevant to many quantitative fields ranging from economics to fluid mechanics. In the physical sciences, structures such as metastable and coherent sets, slow relaxation processes, collective variables dominant transition pathways or manifolds and channels of probability flow can be of great importance for understanding and characterizing the kinetic, thermodynamic and mechanistic properties of the system. Deeptime is a general purpose Python library offering various tools to estimate dynamical models based on time-series data including conventional linear learning methods, such as Markov state models (MSMs), Hidden Markov Models and Koopman models, as well as kernel and deep learning approaches such as VAMPnets and deep MSMs. The library is largely compatible with scikit-learn, having a range of Estimator classes for these different models, but in contrast to scikit-learn also provides deep Model classes, e.g. in the case of an MSM, which provide a multitude of analysis methods to compute interesting thermodynamic, kinetic and dynamical quantities, such as free energies, relaxation times and transition paths. The library is designed for ease of use but also easily maintainable and extensible code. In this paper we introduce the main features and structure of the deeptime software.

From Fourier to Koopman: Spectral Methods for Long-term Time Series Prediction

We propose spectral methods for long-term forecasting of temporal signals stemming from linear and nonlinear quasi-periodic dynamical systems. For linear signals, we introduce an algorithm with similarities to the Fourier transform but which does not rely on periodicity assumptions, allowing for forecasting given potentially arbitrary sampling intervals. We then extend this algorithm to handle nonlinearities by leveraging Koopman theory. The resulting algorithm performs a spectral decomposition in a nonlinear, data-dependent basis. The optimization objective for both algorithms is highly non-convex. However, expressing the objective in the frequency domain allows us to compute global optima of the error surface in a scalable and efficient manner, partially by exploiting the computational properties of the Fast Fourier Transform. Because of their close relation to Bayesian Spectral Analysis, uncertainty quantification metrics are a natural byproduct of the spectral forecasting methods. We extensively benchmark these algorithms against other leading forecasting methods on a range of synthetic experiments as well as in the context of real-world power systems and fluid flows.