Deep networks for system identification: a Survey

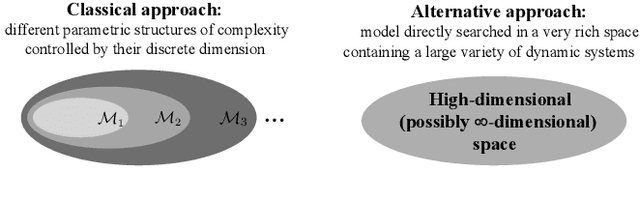
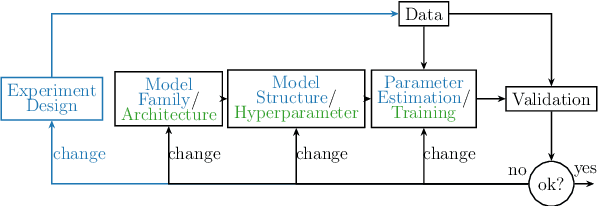
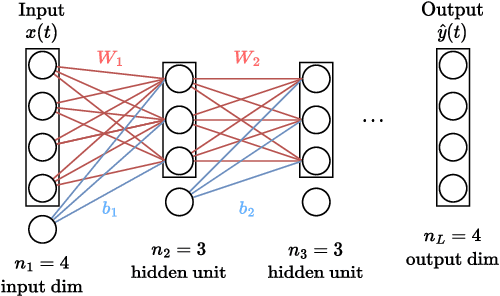
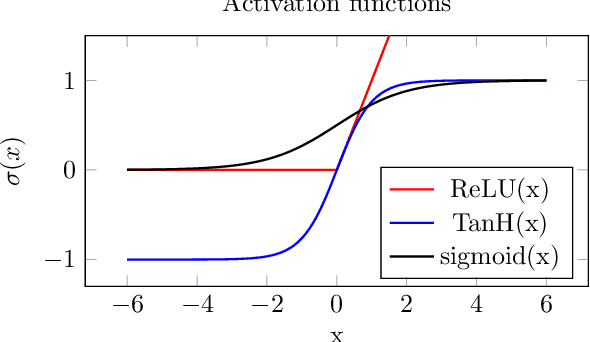
Deep learning is a topic of considerable current interest. The availability of massive data collections and powerful software resources has led to an impressive amount of results in many application areas that reveal essential but hidden properties of the observations. System identification learns mathematical descriptions of dynamic systems from input-output data and can thus benefit from the advances of deep neural networks to enrich the possible range of models to choose from. For this reason, we provide a survey of deep learning from a system identification perspective. We cover a wide spectrum of topics to enable researchers to understand the methods, providing rigorous practical and theoretical insights into the benefits and challenges of using them. The main aim of the identified model is to predict new data from previous observations. This can be achieved with different deep learning based modelling techniques and we discuss architectures commonly adopted in the literature, like feedforward, convolutional, and recurrent networks. Their parameters have to be estimated from past data trying to optimize the prediction performance. For this purpose, we discuss a specific set of first-order optimization tools that is emerged as efficient. The survey then draws connections to the well-studied area of kernel-based methods. They control the data fit by regularization terms that penalize models not in line with prior assumptions. We illustrate how to cast them in deep architectures to obtain deep kernel-based methods. The success of deep learning also resulted in surprising empirical observations, like the counter-intuitive behaviour of models with many parameters. We discuss the role of overparameterized models, including their connection to kernels, as well as implicit regularization mechanisms which affect generalization, specifically the interesting phenomena of benign overfitting ...

Spatiotemporal k-means

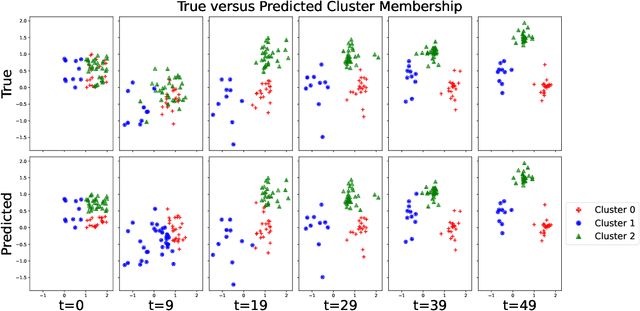
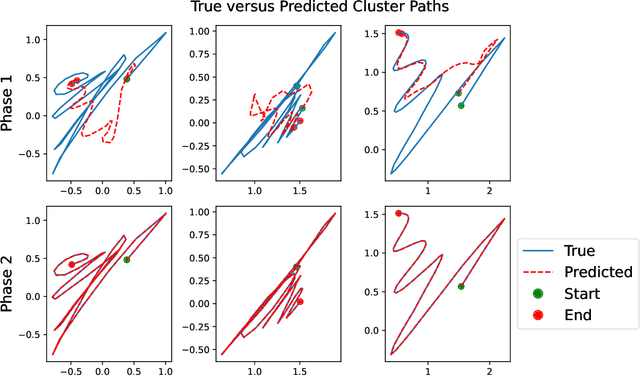
Spatiotemporal data is readily available due to emerging sensor and data acquisition technologies that track the positions of moving objects of interest. Spatiotemporal clustering addresses the need to efficiently discover patterns and trends in moving object behavior without human supervision. One application of interest is the discovery of moving clusters, where clusters have a static identity, but their location and content can change over time. We propose a two phase spatiotemporal clustering method called spatiotemporal k-means (STKM) that is able to analyze the multi-scale relationships within spatiotemporal data. Phase 1 of STKM frames the moving cluster problem as the minimization of an objective function unified over space and time. It outputs the short-term associations between objects and is uniquely able to track dynamic cluster centers with minimal parameter tuning and without post-processing. Phase 2 outputs the long-term associations and can be applied to any method that provides a cluster label for each object at every point in time. We evaluate STKM against baseline methods on a recently developed benchmark dataset and show that STKM outperforms existing methods, particularly in the low-data domain, with significant performance improvements demonstrated for common evaluation metrics on the moving cluster problem.

Theoretical Advances in Current Estimation and Navigation from a Glider-Based Acoustic Doppler Current Profiler (ADCP)

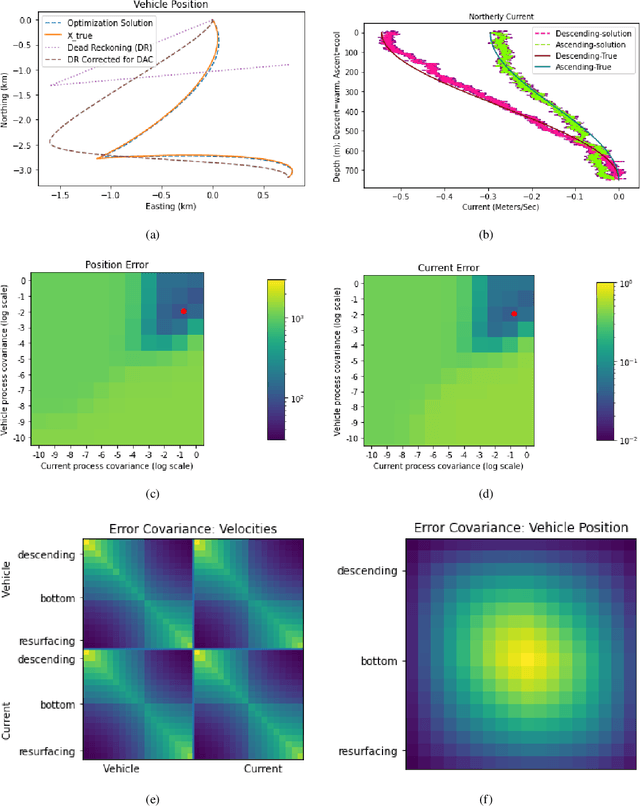
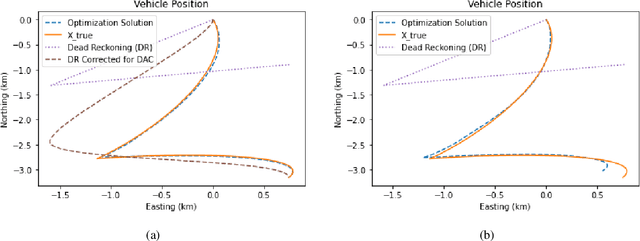
We examine acoustic Doppler current profiler (ADCP) measurements from underwater gliders to determine glider position, glider velocity, and subsurface current. ADCPs, however, do not directly observe the quantities of interest; instead, they measure the relative motion of the vehicle and the water column. We examine the lineage of mathematical innovations that have previously been applied to this problem, discovering an unstated but incorrect assumption of independence. We reframe a recent method to form a joint probability model of current and vehicle navigation, which allows us to correct this assumption and extend the classic Kalman smoothing method. Detailed simulations affirm the efficacy of our approach for computing estimates and their uncertainty. The joint model developed here sets the stage for future work to incorporate constraints, range measurements, and robust statistical modeling.

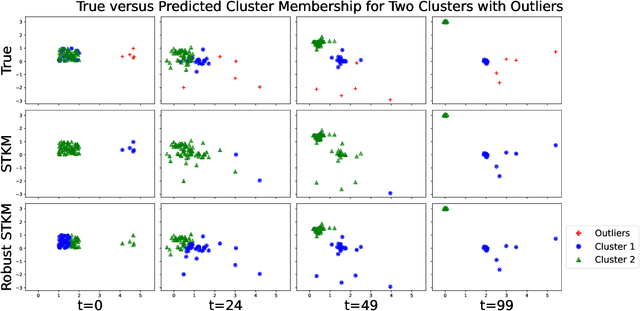
Robust Trimmed k-means

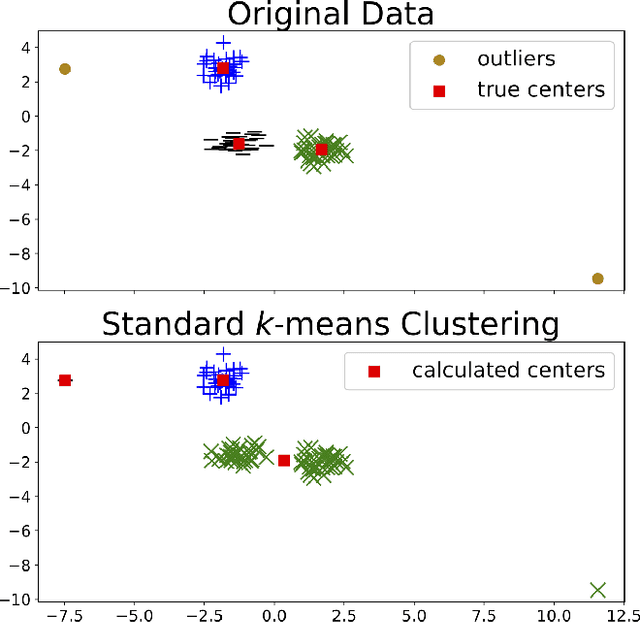
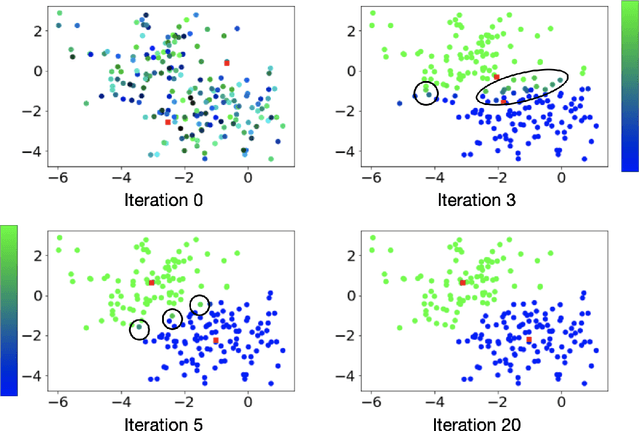
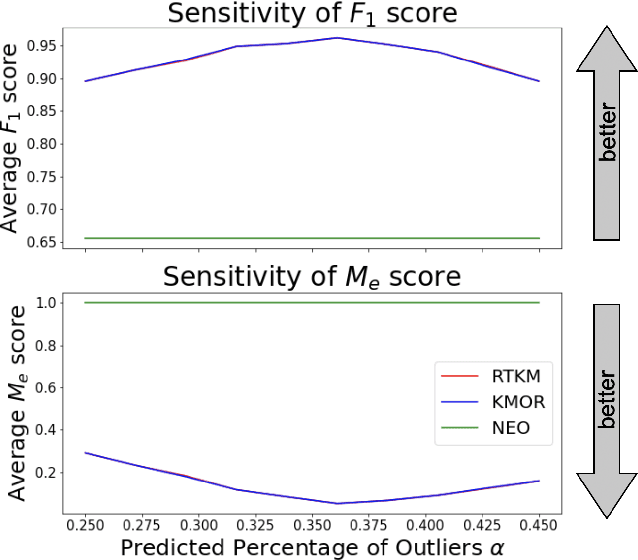
Clustering is a fundamental tool in unsupervised learning, used to group objects by distinguishing between similar and dissimilar features of a given data set. One of the most common clustering algorithms is k-means. Unfortunately, when dealing with real-world data many traditional clustering algorithms are compromised by lack of clear separation between groups, noisy observations, and/or outlying data points. Thus, robust statistical algorithms are required for successful data analytics. Current methods that robustify k-means clustering are specialized for either single or multi-membership data, but do not perform competitively in both cases. We propose an extension of the k-means algorithm, which we call Robust Trimmed k-means (RTKM) that simultaneously identifies outliers and clusters points and can be applied to either single- or multi-membership data. We test RTKM on various real-world datasets and show that RTKM performs competitively with other methods on single membership data with outliers and multi-membership data without outliers. We also show that RTKM leverages its relative advantages to outperform other methods on multi-membership data containing outliers.

A feasibility study of a hyperparameter tuning approach to automated inverse planning in radiotherapy

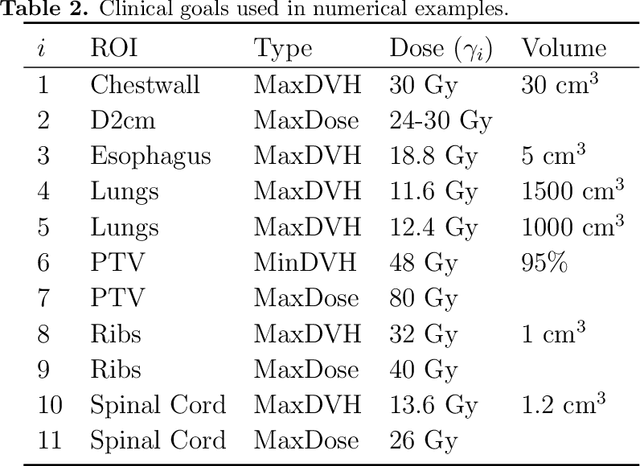
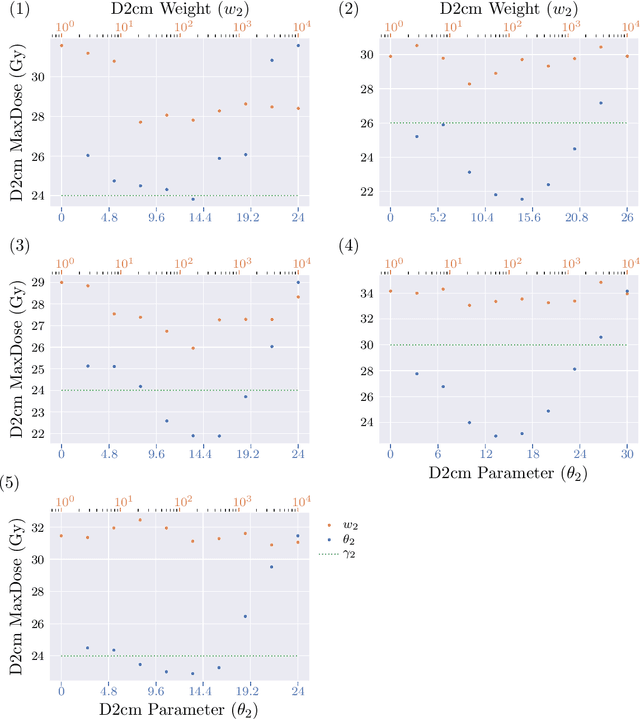
Radiotherapy inverse planning requires treatment planners to modify multiple parameters in the objective function to produce clinically acceptable plans. Due to manual steps in this process, plan quality can vary widely depending on planning time available and planner's skills. The purpose of this study is to automate the inverse planning process to reduce active planning time while maintaining plan quality. We propose a hyperparameter tuning approach for automated inverse planning, where a treatment plan utility is maximized with respect to the limit dose parameters and weights of each organ-at-risk (OAR) objective. Using 6 patient cases, we investigated the impact of the choice of dose parameters, random and Bayesian search methods, and utility function form on planning time and plan quality. For given parameters, the plan was optimized in RayStation, using the scripting interface to obtain the dose distributions deliverable. We normalized all plans to have the same target coverage and compared the OAR dose metrics in the automatically generated plans with those in the manually generated clinical plans. Using 100 samples was found to produce satisfactory plan quality, and the average planning time was 2.3 hours. The OAR doses in the automatically generated plans were lower than the clinical plans by up to 76.8%. When the OAR doses were larger than the clinical plans, they were still between 0.57% above and 98.9% below the limit doses, indicating they are clinically acceptable. For a challenging case, a dimensionality reduction strategy produced a 92.9% higher utility using only 38.5% of the time needed to optimize over the original problem. This study demonstrates our hyperparameter tuning framework for automated inverse planning can significantly reduce the treatment planner's planning time with plan quality that is similar to or better than manually generated plans.

Analysis of Truncated Orthogonal Iteration for Sparse Eigenvector Problems

A wide range of problems in computational science and engineering require estimation of sparse eigenvectors for high dimensional systems. Here, we propose two variants of the Truncated Orthogonal Iteration to compute multiple leading eigenvectors with sparsity constraints simultaneously. We establish numerical convergence results for the proposed algorithms using a perturbation framework, and extend our analysis to other existing alternatives for sparse eigenvector estimation. We then apply our algorithms to solve the sparse principle component analysis problem for a wide range of test datasets, from simple simulations to real-world datasets including MNIST, sea surface temperature and 20 newsgroups. In all these cases, we show that the new methods get state of the art results quickly and with minimal parameter tuning.

Time-varying Autoregression with Low Rank Tensors

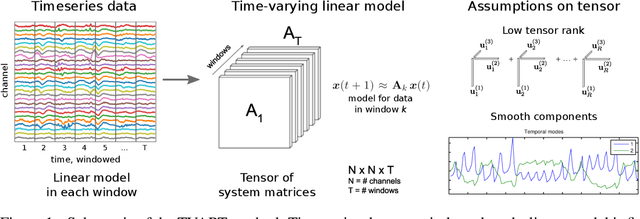
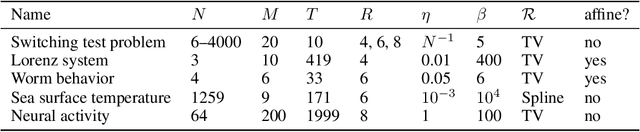
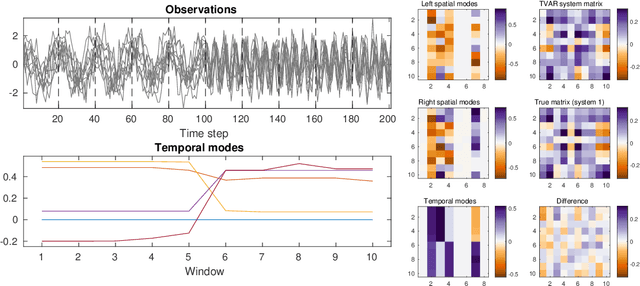
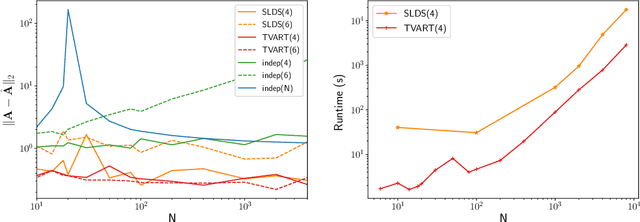
We present a windowed technique to learn parsimonious time-varying autoregressive models from multivariate timeseries. This unsupervised method uncovers spatiotemporal structure in data via non-smooth and non-convex optimization. In each time window, we assume the data follow a linear model parameterized by a potentially different system matrix, and we model this stack of system matrices as a low rank tensor. Because of its structure, the model is scalable to high-dimensional data and can easily incorporate priors such as smoothness over time. We find the components of the tensor using alternating minimization and prove that any stationary point of this algorithm is a local minimum. In a test case, our method identifies the true rank of a switching linear system in the presence of noise. We illustrate our model's utility and superior scalability over extant methods when applied to several synthetic and real examples, including a nonlinear dynamical system, worm behavior, sea surface temperature, and monkey brain recordings.

Basis Pursuit Denoise with Nonsmooth Constraints

Level-set optimization formulations with data-driven constraints minimize a regularization functional subject to matching observations to a given error level. These formulations are widely used, particularly for matrix completion and sparsity promotion in data interpolation and denoising. The misfit level is typically measured in the l2 norm, or other smooth metrics. In this paper, we present a new flexible algorithmic framework that targets nonsmooth level-set constraints, including L1, Linf, and even L0 norms. These constraints give greater flexibility for modeling deviations in observation and denoising, and have significant impact on the solution. Measuring error in the L1 and L0 norms makes the result more robust to large outliers, while matching many observations exactly. We demonstrate the approach for basis pursuit denoise (BPDN) problems as well as for extensions of BPDN to matrix factorization, with applications to interpolation and denoising of 5D seismic data. The new methods are particularly promising for seismic applications, where the amplitude in the data varies significantly, and measurement noise in low-amplitude regions can wreak havoc for standard Gaussian error models.

Variable projection without smoothness

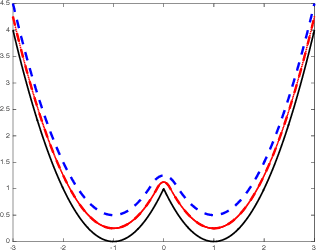
Variable projection solves structured optimization problems by completely minimizing over a subset of the variables while iterating over the remaining variables. Over the last 30 years, the technique has been widely used, with empirical and theoretical results demonstrating both greater efficacy and greater stability compared to competing approaches. Classic examples have exploited closed form projections and smoothness of the objective function. We extend the approach to broader settings, where the projection subproblems can be nonsmooth, and can only be solved inexactly by iterative methods. We present a few case studies on problems occurring frequently in machine-learning and high-dimensional inference.

Learning Nonlinear Brain Dynamics: van der Pol Meets LSTM

Many real-world data sets, especially in biology, are produced by highly multivariate and nonlinear complex dynamical systems. In this paper, we focus on brain imaging data, including both calcium imaging and functional MRI data. Standard vector-autoregressive models are limited by their linearity assumptions, while nonlinear general-purpose, large-scale temporal models, such as LSTM networks, typically require large amounts of training data, not always readily available in biological applications; furthermore, such models have limited interpretability. We introduce here a novel approach for learning a nonlinear differential equation model aimed at capturing brain dynamics. Specifically, we propose a variable-projection optimization approach to estimate the parameters of the multivariate (coupled) van der Pol oscillator, and demonstrate that such a model can accurately represent nonlinear dynamics of the brain data. Furthermore, in order to improve the predictive accuracy when forecasting future brain-activity time series, we use this analytical model as an unlimited source of simulated data for pretraining LSTM; such model-specific data augmentation approach consistently improves LSTM performance on both calcium and fMRI imaging data.