Robust Trimmed k-means
Paper and Code
Aug 16, 2021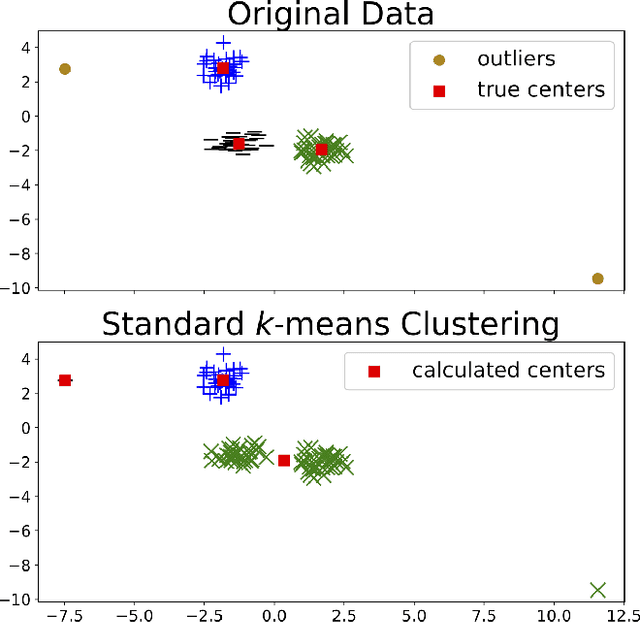

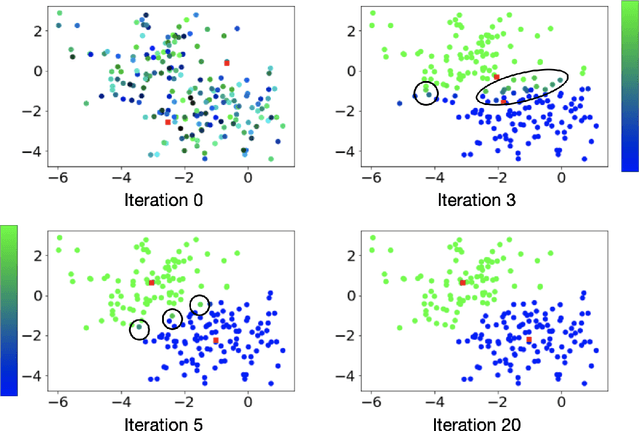
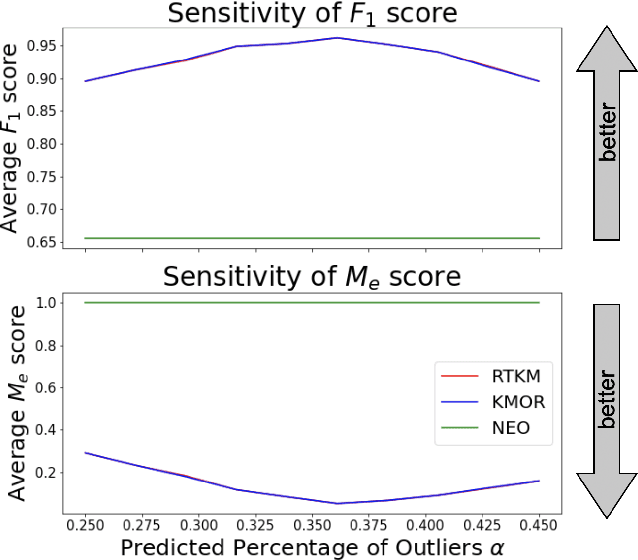
Clustering is a fundamental tool in unsupervised learning, used to group objects by distinguishing between similar and dissimilar features of a given data set. One of the most common clustering algorithms is k-means. Unfortunately, when dealing with real-world data many traditional clustering algorithms are compromised by lack of clear separation between groups, noisy observations, and/or outlying data points. Thus, robust statistical algorithms are required for successful data analytics. Current methods that robustify k-means clustering are specialized for either single or multi-membership data, but do not perform competitively in both cases. We propose an extension of the k-means algorithm, which we call Robust Trimmed k-means (RTKM) that simultaneously identifies outliers and clusters points and can be applied to either single- or multi-membership data. We test RTKM on various real-world datasets and show that RTKM performs competitively with other methods on single membership data with outliers and multi-membership data without outliers. We also show that RTKM leverages its relative advantages to outperform other methods on multi-membership data containing outliers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge