Spatiotemporal k-means

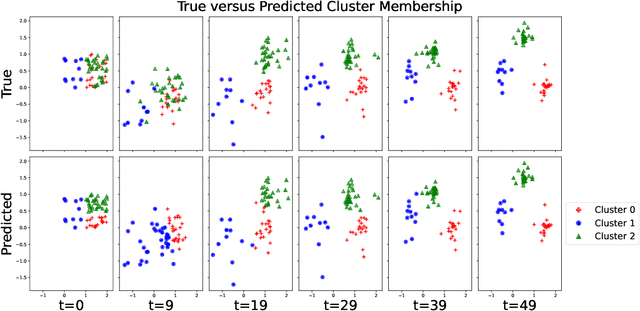
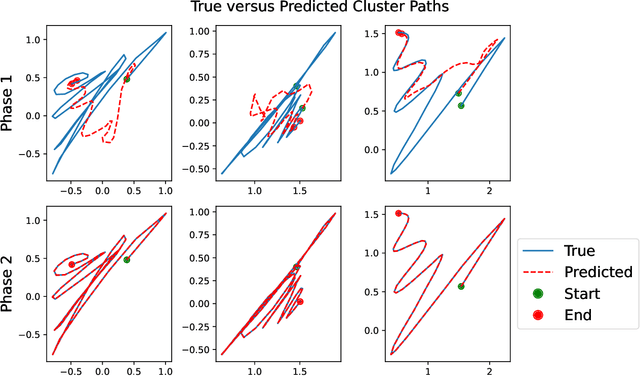
Spatiotemporal data is readily available due to emerging sensor and data acquisition technologies that track the positions of moving objects of interest. Spatiotemporal clustering addresses the need to efficiently discover patterns and trends in moving object behavior without human supervision. One application of interest is the discovery of moving clusters, where clusters have a static identity, but their location and content can change over time. We propose a two phase spatiotemporal clustering method called spatiotemporal k-means (STKM) that is able to analyze the multi-scale relationships within spatiotemporal data. Phase 1 of STKM frames the moving cluster problem as the minimization of an objective function unified over space and time. It outputs the short-term associations between objects and is uniquely able to track dynamic cluster centers with minimal parameter tuning and without post-processing. Phase 2 outputs the long-term associations and can be applied to any method that provides a cluster label for each object at every point in time. We evaluate STKM against baseline methods on a recently developed benchmark dataset and show that STKM outperforms existing methods, particularly in the low-data domain, with significant performance improvements demonstrated for common evaluation metrics on the moving cluster problem.

Robust Trimmed k-means

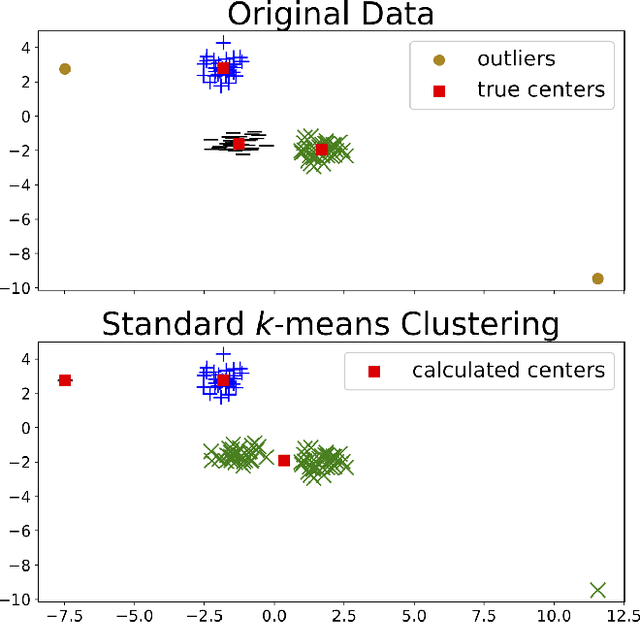
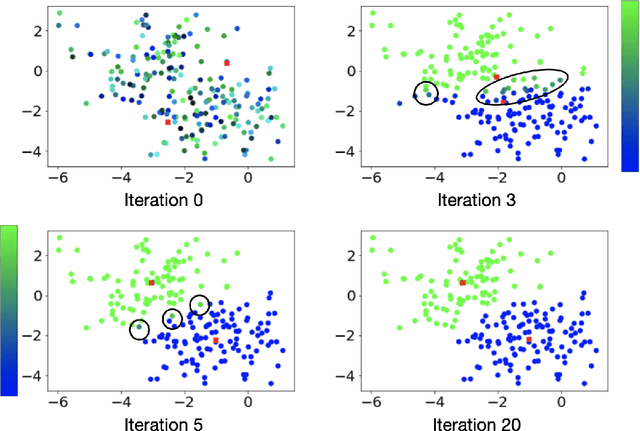
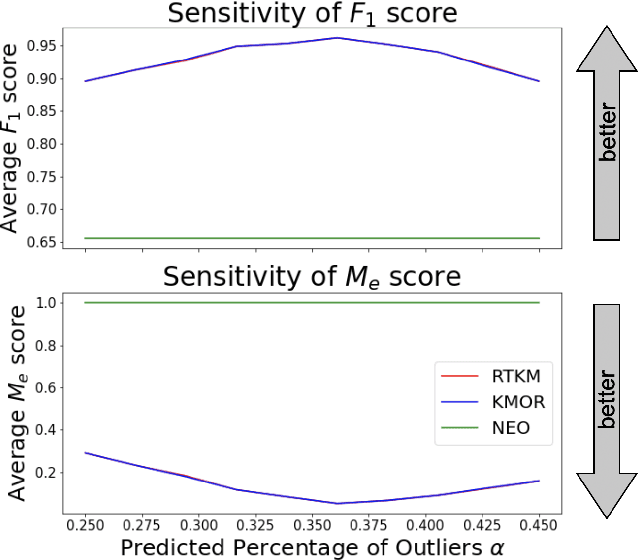
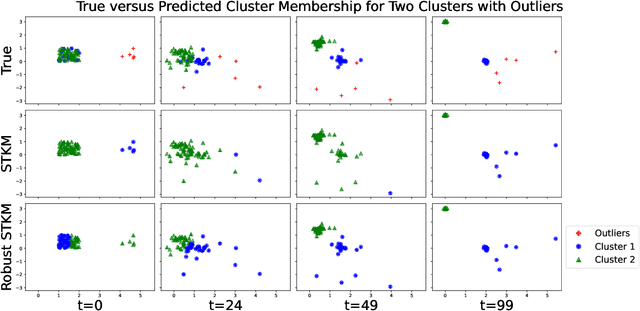
Clustering is a fundamental tool in unsupervised learning, used to group objects by distinguishing between similar and dissimilar features of a given data set. One of the most common clustering algorithms is k-means. Unfortunately, when dealing with real-world data many traditional clustering algorithms are compromised by lack of clear separation between groups, noisy observations, and/or outlying data points. Thus, robust statistical algorithms are required for successful data analytics. Current methods that robustify k-means clustering are specialized for either single or multi-membership data, but do not perform competitively in both cases. We propose an extension of the k-means algorithm, which we call Robust Trimmed k-means (RTKM) that simultaneously identifies outliers and clusters points and can be applied to either single- or multi-membership data. We test RTKM on various real-world datasets and show that RTKM performs competitively with other methods on single membership data with outliers and multi-membership data without outliers. We also show that RTKM leverages its relative advantages to outperform other methods on multi-membership data containing outliers.