Learning Nonlinear Brain Dynamics: van der Pol Meets LSTM

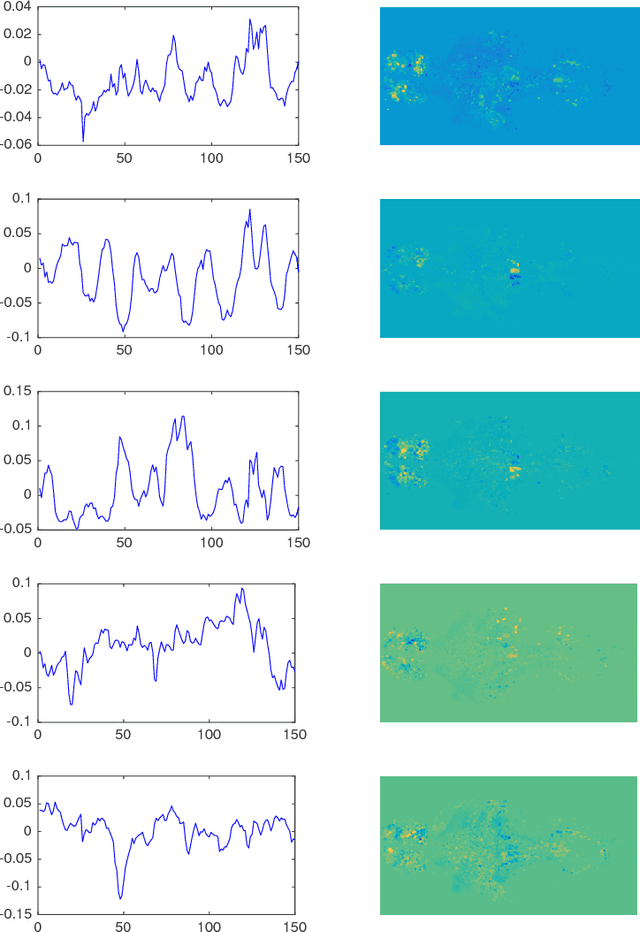
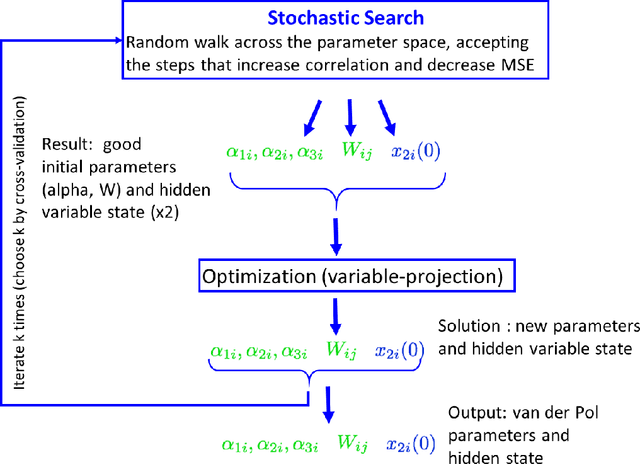
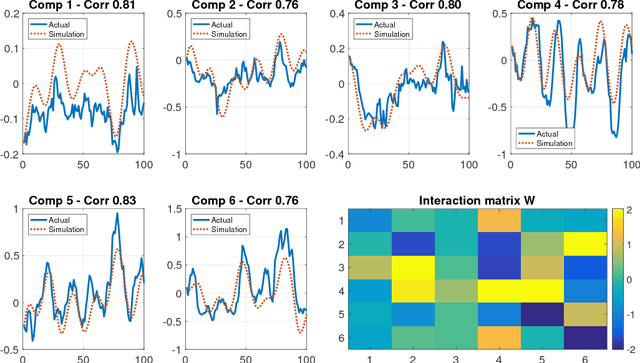
Many real-world data sets, especially in biology, are produced by highly multivariate and nonlinear complex dynamical systems. In this paper, we focus on brain imaging data, including both calcium imaging and functional MRI data. Standard vector-autoregressive models are limited by their linearity assumptions, while nonlinear general-purpose, large-scale temporal models, such as LSTM networks, typically require large amounts of training data, not always readily available in biological applications; furthermore, such models have limited interpretability. We introduce here a novel approach for learning a nonlinear differential equation model aimed at capturing brain dynamics. Specifically, we propose a variable-projection optimization approach to estimate the parameters of the multivariate (coupled) van der Pol oscillator, and demonstrate that such a model can accurately represent nonlinear dynamics of the brain data. Furthermore, in order to improve the predictive accuracy when forecasting future brain-activity time series, we use this analytical model as an unlimited source of simulated data for pretraining LSTM; such model-specific data augmentation approach consistently improves LSTM performance on both calcium and fMRI imaging data.