Spectral gap-based deterministic tensor completion

Tensor completion is a core machine learning algorithm used in recommender systems and other domains with missing data. While the matrix case is well-understood, theoretical results for tensor problems are limited, particularly when the sampling patterns are deterministic. Here we bound the generalization error of the solutions of two tensor completion methods, Poisson loss and atomic norm minimization, providing tighter bounds in terms of the target tensor rank. If the ground-truth tensor is order $t$ with CP-rank $r$, the dependence on $r$ is improved from $r^{2(t-1)(t^2-t-1)}$ in arXiv:1910.10692 to $r^{2(t-1)(3t-5)}$. The error in our bounds is deterministically controlled by the spectral gap of the sampling sparsity pattern. We also prove several new properties for the atomic tensor norm, reducing the rank dependence from $r^{3t-3}$ in arXiv:1711.04965 to $r^{3t-5}$ under random sampling schemes. A limitation is that atomic norm minimization, while theoretically interesting, leads to inefficient algorithms. However, numerical experiments illustrate the dependence of the reconstruction error on the spectral gap for the practical max-quasinorm, ridge penalty, and Poisson loss minimization algorithms. This view through the spectral gap is a promising window for further study of tensor algorithms.

Deterministic tensor completion with hypergraph expanders

We provide a novel analysis of low rank tensor completion based on hypergraph expanders. As a proxy for rank, we minimize the max-quasinorm of the tensor, introduced by Ghadermarzy, Plan, and Yilmaz (2018), which generalizes the max-norm for matrices. Our analysis is deterministic and shows that the number of samples required to recover an order-$t$ tensor with at most $n$ entries per dimension is linear in $n$, under the assumption that the rank and order of the tensor are $O(1)$. As steps in our proof, we find an improved expander mixing lemma for a $t$-partite, $t$-uniform regular hypergraph model and prove several new properties about tensor max-quasinorm. To the best of our knowledge, this is the first deterministic analysis of tensor completion.

Additive function approximation in the brain

Many biological learning systems such as the mushroom body, hippocampus, and cerebellum are built from sparsely connected networks of neurons. For a new understanding of such networks, we study the function spaces induced by sparse random features and characterize what functions may and may not be learned. A network with $d$ inputs per neuron is found to be equivalent to an additive model of order $d$, whereas with a degree distribution the network combines additive terms of different orders. We identify three specific advantages of sparsity: additive function approximation is a powerful inductive bias that limits the curse of dimensionality, sparse networks are stable to outlier noise in the inputs, and sparse random features are scalable. Thus, even simple brain architectures can be powerful function approximators. Finally, we hope that this work helps popularize kernel theories of networks among computational neuroscientists.

Time-varying Autoregression with Low Rank Tensors

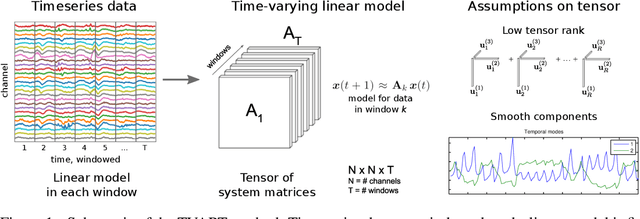
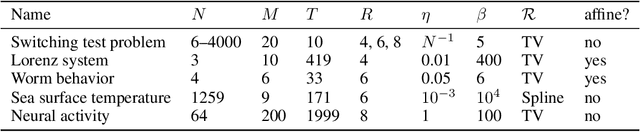
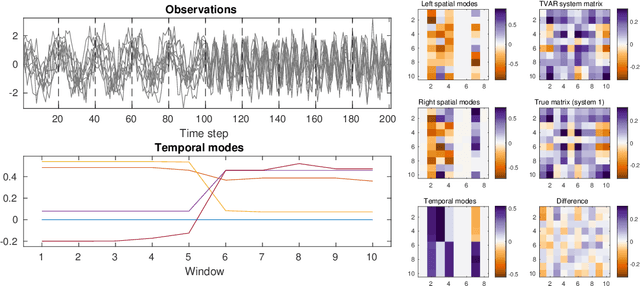
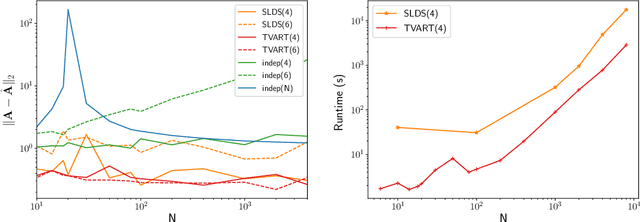
We present a windowed technique to learn parsimonious time-varying autoregressive models from multivariate timeseries. This unsupervised method uncovers spatiotemporal structure in data via non-smooth and non-convex optimization. In each time window, we assume the data follow a linear model parameterized by a potentially different system matrix, and we model this stack of system matrices as a low rank tensor. Because of its structure, the model is scalable to high-dimensional data and can easily incorporate priors such as smoothness over time. We find the components of the tensor using alternating minimization and prove that any stationary point of this algorithm is a local minimum. In a test case, our method identifies the true rank of a switching linear system in the presence of noise. We illustrate our model's utility and superior scalability over extant methods when applied to several synthetic and real examples, including a nonlinear dynamical system, worm behavior, sea surface temperature, and monkey brain recordings.

Human language reveals a universal positivity bias

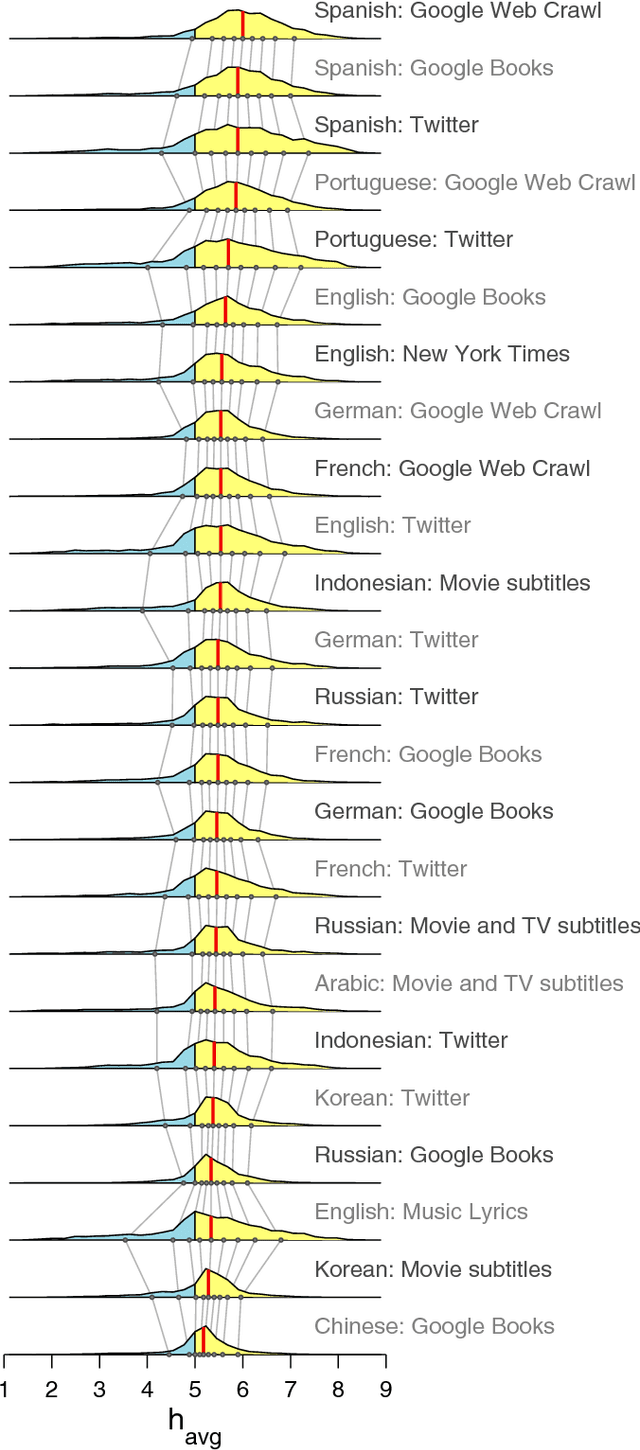
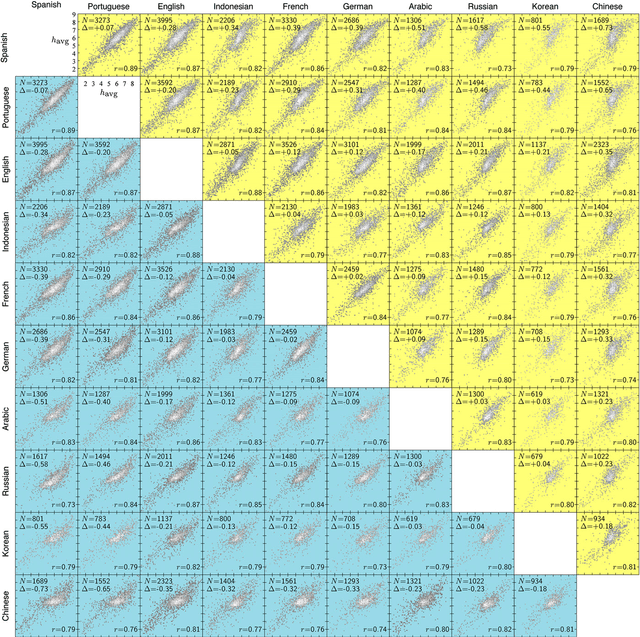
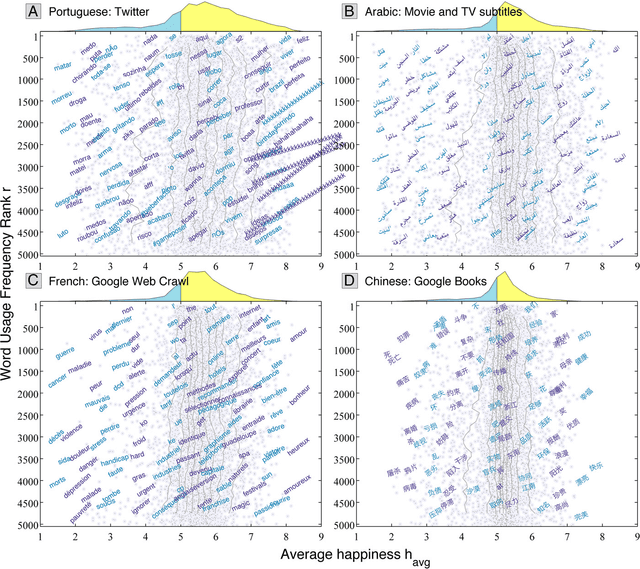
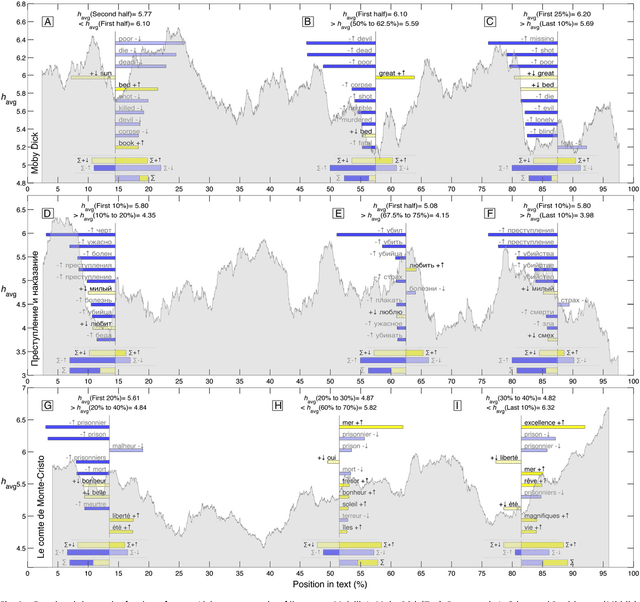
Using human evaluation of 100,000 words spread across 24 corpora in 10 languages diverse in origin and culture, we present evidence of a deep imprint of human sociality in language, observing that (1) the words of natural human language possess a universal positivity bias; (2) the estimated emotional content of words is consistent between languages under translation; and (3) this positivity bias is strongly independent of frequency of word usage. Alongside these general regularities, we describe inter-language variations in the emotional spectrum of languages which allow us to rank corpora. We also show how our word evaluations can be used to construct physical-like instruments for both real-time and offline measurement of the emotional content of large-scale texts.

Positivity of the English language

Over the last million years, human language has emerged and evolved as a fundamental instrument of social communication and semiotic representation. People use language in part to convey emotional information, leading to the central and contingent questions: (1) What is the emotional spectrum of natural language? and (2) Are natural languages neutrally, positively, or negatively biased? Here, we report that the human-perceived positivity of over 10,000 of the most frequently used English words exhibits a clear positive bias. More deeply, we characterize and quantify distributions of word positivity for four large and distinct corpora, demonstrating that their form is broadly invariant with respect to frequency of word use.