Simple and Nearly-Optimal Sampling for Rank-1 Tensor Completion via Gauss-Jordan

We revisit the sample and computational complexity of completing a rank-1 tensor in $\otimes_{i=1}^{N} \mathbb{R}^{d}$, given a uniformly sampled subset of its entries. We present a characterization of the problem (i.e. nonzero entries) which admits an algorithm amounting to Gauss-Jordan on a pair of random linear systems. For example, when $N = \Theta(1)$, we prove it uses no more than $m = O(d^2 \log d)$ samples and runs in $O(md^2)$ time. Moreover, we show any algorithm requires $\Omega(d\log d)$ samples. By contrast, existing upper bounds on the sample complexity are at least as large as $d^{1.5} \mu^{\Omega(1)} \log^{\Omega(1)} d$, where $\mu$ can be $\Theta(d)$ in the worst case. Prior work obtained these looser guarantees in higher rank versions of our problem, and tend to involve more complicated algorithms.

Spectral gap-based deterministic tensor completion

Tensor completion is a core machine learning algorithm used in recommender systems and other domains with missing data. While the matrix case is well-understood, theoretical results for tensor problems are limited, particularly when the sampling patterns are deterministic. Here we bound the generalization error of the solutions of two tensor completion methods, Poisson loss and atomic norm minimization, providing tighter bounds in terms of the target tensor rank. If the ground-truth tensor is order $t$ with CP-rank $r$, the dependence on $r$ is improved from $r^{2(t-1)(t^2-t-1)}$ in arXiv:1910.10692 to $r^{2(t-1)(3t-5)}$. The error in our bounds is deterministically controlled by the spectral gap of the sampling sparsity pattern. We also prove several new properties for the atomic tensor norm, reducing the rank dependence from $r^{3t-3}$ in arXiv:1711.04965 to $r^{3t-5}$ under random sampling schemes. A limitation is that atomic norm minimization, while theoretically interesting, leads to inefficient algorithms. However, numerical experiments illustrate the dependence of the reconstruction error on the spectral gap for the practical max-quasinorm, ridge penalty, and Poisson loss minimization algorithms. This view through the spectral gap is a promising window for further study of tensor algorithms.

Zero-Truncated Poisson Regression for Zero-Inflated Multiway Count Data

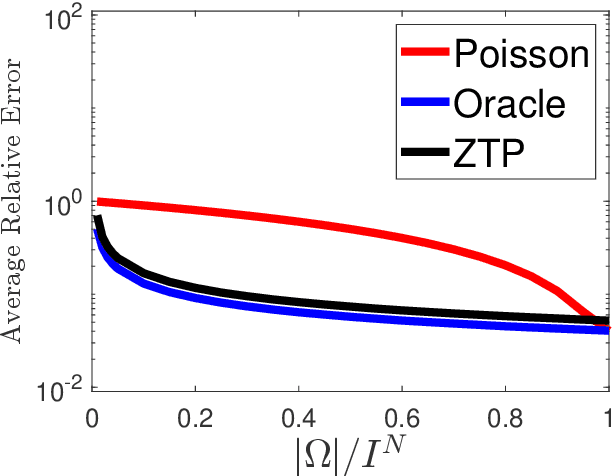
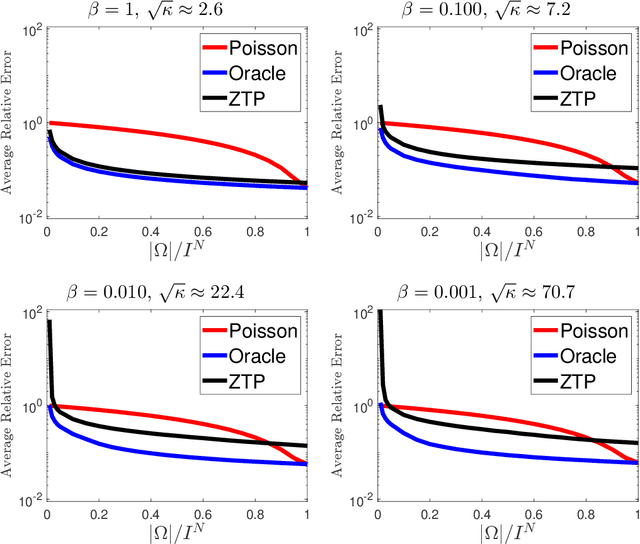
We propose a novel statistical inference paradigm for zero-inflated multiway count data that dispenses with the need to distinguish between true and false zero counts. Our approach ignores all zero entries and applies zero-truncated Poisson regression on the positive counts. Inference is accomplished via tensor completion that imposes low-rank structure on the Poisson parameter space. Our main result shows that an $N$-way rank-$R$ parametric tensor $\boldsymbol{\mathscr{M}}\in(0,\infty)^{I\times \cdots\times I}$ generating Poisson observations can be accurately estimated from approximately $IR^2\log_2^2(I)$ non-zero counts for a nonnegative canonical polyadic decomposition. Several numerical experiments are presented demonstrating that our zero-truncated paradigm is comparable to the ideal scenario where the locations of false zero counts are known a priori.

Beating level-set methods for 3D seismic data interpolation: a primal-dual alternating approach

Acquisition cost is a crucial bottleneck for seismic workflows, and low-rank formulations for data interpolation allow practitioners to `fill in' data volumes from critically subsampled data acquired in the field. Tremendous size of seismic data volumes required for seismic processing remains a major challenge for these techniques. We propose a new approach to solve residual constrained formulations for interpolation. We represent the data volume using matrix factors, and build a block-coordinate algorithm with constrained convex subproblems that are solved with a primal-dual splitting scheme. The new approach is competitive with state of the art level-set algorithms that interchange the role of objectives with constraints. We use the new algorithm to successfully interpolate a large scale 5D seismic data volume, generated from the geologically complex synthetic 3D Compass velocity model, where 80% of the data has been removed.