l1-Norm Minimization with Regula Falsi Type Root Finding Methods

Sparse level-set formulations allow practitioners to find the minimum 1-norm solution subject to likelihood constraints. Prior art requires this constraint to be convex. In this letter, we develop an efficient approach for nonconvex likelihoods, using Regula Falsi root-finding techniques to solve the level-set formulation. Regula Falsi methods are simple, derivative-free, and efficient, and the approach provably extends level-set methods to the broader class of nonconvex inverse problems. Practical performance is illustrated using l1-regularized Student's t inversion, which is a nonconvex approach used to develop outlier-robust formulations.

Data-Driven Aerospace Engineering: Reframing the Industry with Machine Learning

Data science, and machine learning in particular, is rapidly transforming the scientific and industrial landscapes. The aerospace industry is poised to capitalize on big data and machine learning, which excels at solving the types of multi-objective, constrained optimization problems that arise in aircraft design and manufacturing. Indeed, emerging methods in machine learning may be thought of as data-driven optimization techniques that are ideal for high-dimensional, non-convex, and constrained, multi-objective optimization problems, and that improve with increasing volumes of data. In this review, we will explore the opportunities and challenges of integrating data-driven science and engineering into the aerospace industry. Importantly, we will focus on the critical need for interpretable, generalizeable, explainable, and certifiable machine learning techniques for safety-critical applications. This review will include a retrospective, an assessment of the current state-of-the-art, and a roadmap looking forward. Recent algorithmic and technological trends will be explored in the context of critical challenges in aerospace design, manufacturing, verification, validation, and services. In addition, we will explore this landscape through several case studies in the aerospace industry. This document is the result of close collaboration between UW and Boeing to summarize past efforts and outline future opportunities.

Trimmed Constrained Mixed Effects Models: Formulations and Algorithms

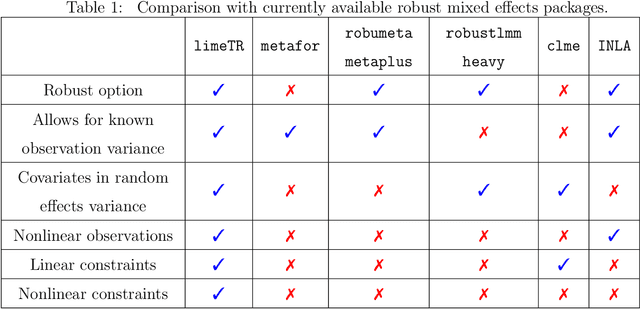
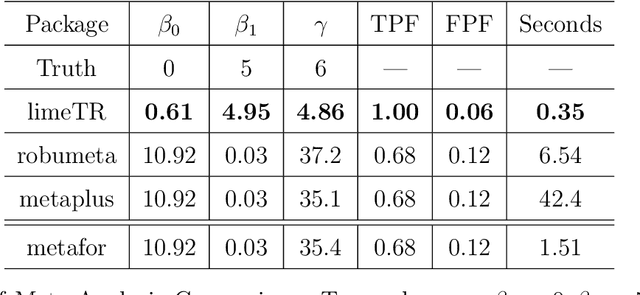
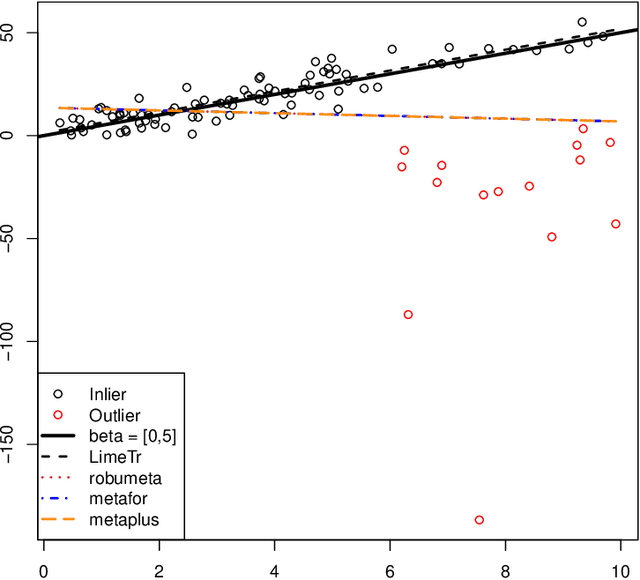
Mixed effects (ME) models inform a vast array of problems in the physical and social sciences, and are pervasive in meta-analysis. We consider ME models where the random effects component is linear. We then develop an efficient approach for a broad problem class that allows nonlinear measurements, priors, and constraints, and finds robust estimates in all of these cases using trimming in the associated marginal likelihood. We illustrate the efficacy of the approach on a range of applications for meta-analysis of global health data. Constraints and priors are used to impose monotonicity, convexity and other characteristics on dose-response relationships, while nonlinear observations enable new epidemiological analyses in place of approximations. Robust extensions ensure that spurious studies do not drive our understanding of between-study heterogeneity. The software accompanying this paper is disseminated as an open-source Python package called limeTR.

A unified sparse optimization framework to learn parsimonious physics-informed models from data

Machine learning (ML) is redefining what is possible in data-intensive fields of science and engineering. However, applying ML to problems in the physical sciences comes with a unique set of challenges: scientists want physically interpretable models that can (i) generalize to predict previously unobserved behaviors, (ii) provide effective forecasting predictions (extrapolation), and (iii) be certifiable. Autonomous systems will necessarily interact with changing and uncertain environments, motivating the need for models that can accurately extrapolate based on physical principles (e.g. Newton's universal second law for classical mechanics, F=ma). Standard ML approaches have shown impressive performance for predicting dynamics in an interpolatory regime, but the resulting models often lack interpretability and fail to generalize. In this paper, we introduce a unified sparse optimization framework that learns governing dynamical systems models from data, selecting relevant terms in the dynamics from a library of possible functions. The resulting models are parsimonious, have physical interpretations, and can generalize to new parameter regimes. Our framework allows the use of non-convex sparsity promoting regularization functions and can be adapted to address key challenges in scientific problems and data sets, including outliers, parametric dependencies, and physical constraints. We show that the approach discovers parsimonious dynamical models on several example systems, including a spiking neuron model. This flexible approach can be tailored to the unique challenges associated with a wide range of applications and data sets, providing a powerful ML-based framework for learning governing models for physical systems from data.

A Unified Framework for Sparse Relaxed Regularized Regression: SR3

Regularized regression problems are ubiquitous in statistical modeling, signal processing, and machine learning. Sparse regression in particular has been instrumental in scientific model discovery, including compressed sensing applications, variable selection, and high-dimensional analysis. We propose a broad framework for sparse relaxed regularized regression, called SR3. The key idea is to solve a relaxation of the regularized problem, which has three advantages over the state-of-the-art: (1) solutions of the relaxed problem are superior with respect to errors, false positives, and conditioning, (2) relaxation allows extremely fast algorithms for both convex and nonconvex formulations, and (3) the methods apply to composite regularizers such as total variation (TV) and its nonconvex variants. We demonstrate the advantages of SR3 (computational efficiency, higher accuracy, faster convergence rates, greater flexibility) across a range of regularized regression problems with synthetic and real data, including applications in compressed sensing, LASSO, matrix completion, TV regularization, and group sparsity. To promote reproducible research, we also provide a companion Matlab package that implements these examples.

Sparse Principal Component Analysis via Variable Projection

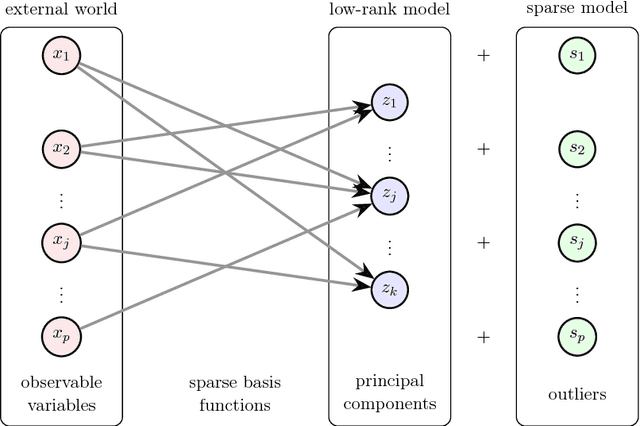
Sparse principal component analysis (SPCA) has emerged as a powerful technique for data analysis, providing improved interpretation of low-rank structures by identifying localized spatial structures in the data and disambiguating between distinct time scales. We demonstrate a robust and scalable SPCA algorithm by formulating it as a value-function optimization problem. This viewpoint leads to a flexible and computationally efficient algorithm. It can further leverage randomized methods from linear algebra to extend the approach to the large-scale (big data) setting. Our proposed innovation also allows for a robust SPCA formulation which can obtain meaningful sparse components in spite of grossly corrupted input data. The proposed algorithms are demonstrated using both synthetic and real world data, showing exceptional computational efficiency and diagnostic performance.

Generalized system identification with stable spline kernels

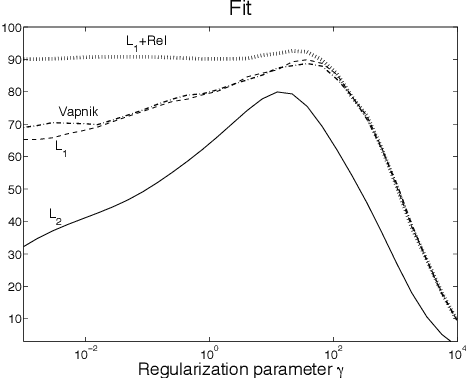
Regularized least-squares approaches have been successfully applied to linear system identification. Recent approaches use quadratic penalty terms on the unknown impulse response defined by stable spline kernels, which control model space complexity by leveraging regularity and bounded-input bounded-output stability. This paper extends linear system identification to a wide class of nonsmooth stable spline estimators, where regularization functionals and data misfits can be selected from a rich set of piecewise linear-quadratic (PLQ) penalties. This class includes the 1-norm, Huber, and Vapnik, in addition to the least-squares penalty. By representing penalties through their conjugates, the modeler can specify any piecewise linear-quadratic penalty for misfit and regularizer, as well as inequality constraints on the response. The interior-point solver we implement (IPsolve) is locally quadratically convergent, with $O(\min(m,n)^2(m+n))$ arithmetic operations per iteration, where $n$ the number of unknown impulse response coefficients and $m$ the number of observed output measurements. IPsolve is competitive with available alternatives for system identification. This is shown by a comparison with TFOCS, libSVM, and the FISTA algorithm. The code is open source (https://github.com/saravkin/IPsolve). The impact of the approach for system identification is illustrated with numerical experiments featuring robust formulations for contaminated data, relaxation systems, nonnegativity and unimodality constraints on the impulse response, and sparsity promoting regularization. Incorporating constraints yields particularly significant improvements.

Computer Assisted Localization of a Heart Arrhythmia

We consider the problem of locating a point-source heart arrhythmia using data from a standard diagnostic procedure, where a reference catheter is placed in the heart, and arrival times from a second diagnostic catheter are recorded as the diagnostic catheter moves around within the heart. We model this situation as a nonconvex feasibility problem, where given a set of arrival times, we look for a source location that is consistent with the available data. We develop a new optimization approach and fast algorithm to obtain online proposals for the next location to suggest to the operator as she collects data. We validate the procedure using a Monte Carlo simulation based on patients' electrophysiological data. The proposed procedure robustly and quickly locates the source of arrhythmias without any prior knowledge of heart anatomy.

Fast Robust Methods for Singular State-Space Models

State-space models are used in a wide range of time series analysis formulations. Kalman filtering and smoothing are work-horse algorithms in these settings. While classic algorithms assume Gaussian errors to simplify estimation, recent advances use a broader range of optimization formulations to allow outlier-robust estimation, as well as constraints to capture prior information. Here we develop methods on state-space models where either innovations or error covariances may be singular. These models frequently arise in navigation (e.g. for `colored noise' models or deterministic integrals) and are ubiquitous in auto-correlated time series models such as ARMA. We reformulate all state-space models (singular as well as nonsinguar) as constrained convex optimization problems, and develop an efficient algorithm for this reformulation. The convergence rate is {\it locally linear}, with constants that do not depend on the conditioning of the problem. Numerical comparisons show that the new approach outperforms competing approaches for {\it nonsingular} models, including state of the art interior point (IP) methods. IP methods converge at superlinear rates; we expect them to dominate. However, the steep rate of the proposed approach (independent of problem conditioning) combined with cheap iterations wins against IP in a run-time comparison. We therefore suggest that the proposed approach be the {\it default choice} for estimating state space models outside of the Gaussian context, regardless of whether the error covariances are singular or not.

Mean Reverting Portfolios via Penalized OU-Likelihood Estimation

We study an optimization-based approach to con- struct a mean-reverting portfolio of assets. Our objectives are threefold: (1) design a portfolio that is well-represented by an Ornstein-Uhlenbeck process with parameters estimated by maximum likelihood, (2) select portfolios with desirable characteristics of high mean reversion and low variance, and (3) select a parsimonious portfolio, i.e. find a small subset of a larger universe of assets that can be used for long and short positions. We present the full problem formulation, a specialized algorithm that exploits partial minimization, and numerical examples using both simulated and empirical price data.