Sparse Principal Component Analysis via Variable Projection

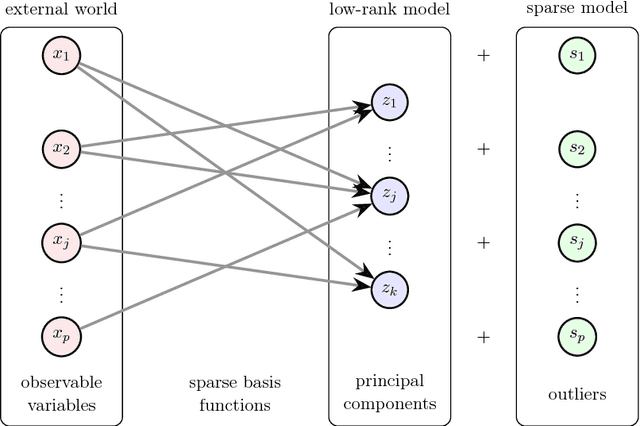
Sparse principal component analysis (SPCA) has emerged as a powerful technique for data analysis, providing improved interpretation of low-rank structures by identifying localized spatial structures in the data and disambiguating between distinct time scales. We demonstrate a robust and scalable SPCA algorithm by formulating it as a value-function optimization problem. This viewpoint leads to a flexible and computationally efficient algorithm. It can further leverage randomized methods from linear algebra to extend the approach to the large-scale (big data) setting. Our proposed innovation also allows for a robust SPCA formulation which can obtain meaningful sparse components in spite of grossly corrupted input data. The proposed algorithms are demonstrated using both synthetic and real world data, showing exceptional computational efficiency and diagnostic performance.