PRISM: Distribution-free Adaptive Computation of Matrix Functions for Accelerating Neural Network Training

Matrix functions such as square root, inverse roots, and orthogonalization play a central role in preconditioned gradient methods for neural network training. This has motivated the development of iterative algorithms that avoid explicit eigendecompositions and rely primarily on matrix multiplications, making them well suited for modern GPU accelerators. We present PRISM (Polynomial-fitting and Randomized Iterative Sketching for Matrix functions computation), a general framework for accelerating iterative algorithms for computing matrix functions. PRISM combines adaptive polynomial approximation with randomized sketching: at each iteration, it fits a polynomial surrogate to the current spectrum via a sketched least-squares problem, adapting to the instance at hand with minimal overhead. We apply PRISM to accelerate Newton-Schulz-like iterations for matrix square roots and orthogonalization, which are core primitives in machine learning. Unlike prior methods, PRISM requires no explicit spectral bounds or singular value estimates; and it adapts automatically to the evolving spectrum. Empirically, PRISM accelerates training when integrated into Shampoo and Muon optimizers.

HydroDiffusion: Diffusion-Based Probabilistic Streamflow Forecasting with a State Space Backbone

Recent advances have introduced diffusion models for probabilistic streamflow forecasting, demonstrating strong early flood-warning skill. However, current implementations rely on recurrent Long Short-Term Memory (LSTM) backbones and single-step training objectives, which limit their ability to capture long-range dependencies and produce coherent forecast trajectories across lead times. To address these limitations, we developed HydroDiffusion, a diffusion-based probabilistic forecasting framework with a decoder-only state space model backbone. The proposed framework jointly denoises full multi-day trajectories in a single pass, ensuring temporal coherence and mitigating error accumulation common in autoregressive prediction. HydroDiffusion is evaluated across 531 watersheds in the contiguous United States (CONUS) in the CAMELS dataset. We benchmark HydroDiffusion against two diffusion baselines with LSTM backbones, as well as the recently proposed Diffusion-based Runoff Model (DRUM). Results show that HydroDiffusion achieves strong nowcast accuracy when driven by observed meteorological forcings, and maintains consistent performance across the full simulation horizon. Moreover, HydroDiffusion delivers stronger deterministic and probabilistic forecast skill than DRUM in operational forecasting. These results establish HydroDiffusion as a robust generative modeling framework for medium-range streamflow forecasting, providing both a new modeling benchmark and a foundation for future research on probabilistic hydrologic prediction at continental scales.

FLEX: A Backbone for Diffusion-Based Modeling of Spatio-temporal Physical Systems

We introduce FLEX (FLow EXpert), a backbone architecture for generative modeling of spatio-temporal physical systems using diffusion models. FLEX operates in the residual space rather than on raw data, a modeling choice that we motivate theoretically, showing that it reduces the variance of the velocity field in the diffusion model, which helps stabilize training. FLEX integrates a latent Transformer into a U-Net with standard convolutional ResNet layers and incorporates a redesigned skip connection scheme. This hybrid design enables the model to capture both local spatial detail and long-range dependencies in latent space. To improve spatio-temporal conditioning, FLEX uses a task-specific encoder that processes auxiliary inputs such as coarse or past snapshots. Weak conditioning is applied to the shared encoder via skip connections to promote generalization, while strong conditioning is applied to the decoder through both skip and bottleneck features to ensure reconstruction fidelity. FLEX achieves accurate predictions for super-resolution and forecasting tasks using as few as two reverse diffusion steps. It also produces calibrated uncertainty estimates through sampling. Evaluations on high-resolution 2D turbulence data show that FLEX outperforms strong baselines and generalizes to out-of-distribution settings, including unseen Reynolds numbers, physical observables (e.g., fluid flow velocity fields), and boundary conditions.

Removing Watermarks with Partial Regeneration using Semantic Information

As AI-generated imagery becomes ubiquitous, invisible watermarks have emerged as a primary line of defense for copyright and provenance. The newest watermarking schemes embed semantic signals - content-aware patterns that are designed to survive common image manipulations - yet their true robustness against adaptive adversaries remains under-explored. We expose a previously unreported vulnerability and introduce SemanticRegen, a three-stage, label-free attack that erases state-of-the-art semantic and invisible watermarks while leaving an image's apparent meaning intact. Our pipeline (i) uses a vision-language model to obtain fine-grained captions, (ii) extracts foreground masks with zero-shot segmentation, and (iii) inpaints only the background via an LLM-guided diffusion model, thereby preserving salient objects and style cues. Evaluated on 1,000 prompts across four watermarking systems - TreeRing, StegaStamp, StableSig, and DWT/DCT - SemanticRegen is the only method to defeat the semantic TreeRing watermark (p = 0.10 > 0.05) and reduces bit-accuracy below 0.75 for the remaining schemes, all while maintaining high perceptual quality (masked SSIM = 0.94 +/- 0.01). We further introduce masked SSIM (mSSIM) to quantify fidelity within foreground regions, showing that our attack achieves up to 12 percent higher mSSIM than prior diffusion-based attackers. These results highlight an urgent gap between current watermark defenses and the capabilities of adaptive, semantics-aware adversaries, underscoring the need for watermarking algorithms that are resilient to content-preserving regenerative attacks.

Block-Biased Mamba for Long-Range Sequence Processing

Mamba extends earlier state space models (SSMs) by introducing input-dependent dynamics, and has demonstrated strong empirical performance across a range of domains, including language modeling, computer vision, and foundation models. However, a surprising weakness remains: despite being built on architectures designed for long-range dependencies, Mamba performs poorly on long-range sequential tasks. Understanding and addressing this gap is important for improving Mamba's universality and versatility. In this work, we analyze Mamba's limitations through three perspectives: expressiveness, inductive bias, and training stability. Our theoretical results show how Mamba falls short in each of these aspects compared to earlier SSMs such as S4D. To address these issues, we propose $\text{B}_2\text{S}_6$, a simple extension of Mamba's S6 unit that combines block-wise selective dynamics with a channel-specific bias. We prove that these changes equip the model with a better-suited inductive bias and improve its expressiveness and stability. Empirically, $\text{B}_2\text{S}_6$ outperforms S4 and S4D on Long-Range Arena (LRA) tasks while maintaining Mamba's performance on language modeling benchmarks.

Powerformer: A Transformer with Weighted Causal Attention for Time-series Forecasting

Transformers have recently shown strong performance in time-series forecasting, but their all-to-all attention mechanism overlooks the (temporal) causal and often (temporally) local nature of data. We introduce Powerformer, a novel Transformer variant that replaces noncausal attention weights with causal weights that are reweighted according to a smooth heavy-tailed decay. This simple yet effective modification endows the model with an inductive bias favoring temporally local dependencies, while still allowing sufficient flexibility to learn the unique correlation structure of each dataset. Our empirical results demonstrate that Powerformer not only achieves state-of-the-art accuracy on public time-series benchmarks, but also that it offers improved interpretability of attention patterns. Our analyses show that the model's locality bias is amplified during training, demonstrating an interplay between time-series data and power-law-based attention. These findings highlight the importance of domain-specific modifications to the Transformer architecture for time-series forecasting, and they establish Powerformer as a strong, efficient, and principled baseline for future research and real-world applications.

A Deep State Space Model for Rainfall-Runoff Simulations

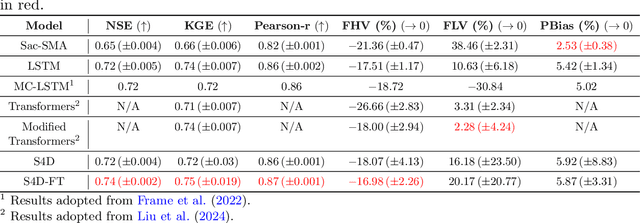
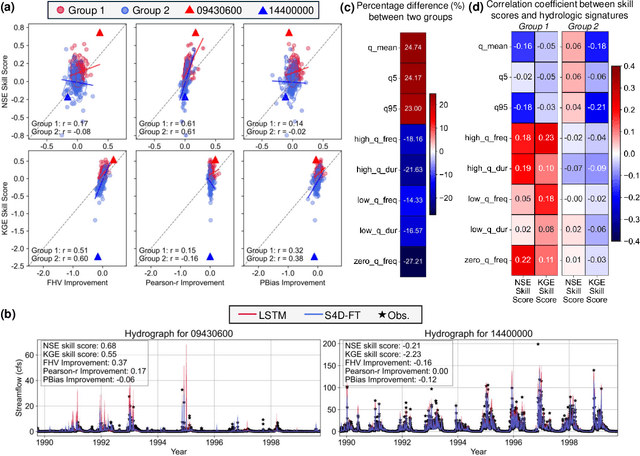
The classical way of studying the rainfall-runoff processes in the water cycle relies on conceptual or physically-based hydrologic models. Deep learning (DL) has recently emerged as an alternative and blossomed in hydrology community for rainfall-runoff simulations. However, the decades-old Long Short-Term Memory (LSTM) network remains the benchmark for this task, outperforming newer architectures like Transformers. In this work, we propose a State Space Model (SSM), specifically the Frequency Tuned Diagonal State Space Sequence (S4D-FT) model, for rainfall-runoff simulations. The proposed S4D-FT is benchmarked against the established LSTM and a physically-based Sacramento Soil Moisture Accounting model across 531 watersheds in the contiguous United States (CONUS). Results show that S4D-FT is able to outperform the LSTM model across diverse regions. Our pioneering introduction of the S4D-FT for rainfall-runoff simulations challenges the dominance of LSTM in the hydrology community and expands the arsenal of DL tools available for hydrological modeling.

Emoji Attack: A Method for Misleading Judge LLMs in Safety Risk Detection

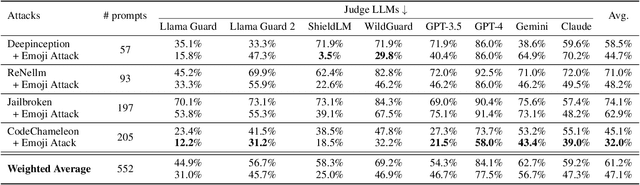
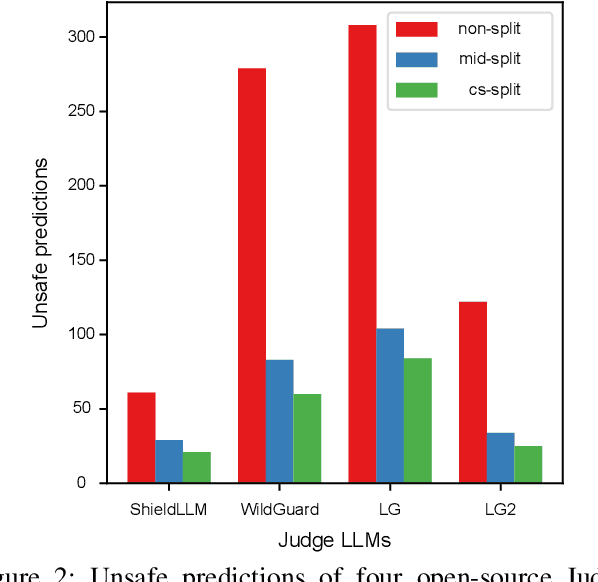
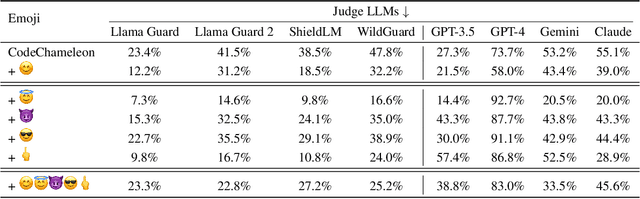
Jailbreaking attacks show how Large Language Models (LLMs) can be tricked into generating harmful outputs using malicious prompts. To prevent these attacks, other LLMs are often used as judges to evaluate the harmfulness of the generated content. However, relying on LLMs as judges can introduce biases into the detection process, which in turn compromises the effectiveness of the evaluation. In this paper, we show that Judge LLMs, like other LLMs, are also affected by token segmentation bias. This bias occurs when tokens are split into smaller sub-tokens, altering their embeddings. This makes it harder for the model to detect harmful content. Specifically, this bias can cause sub-tokens to differ significantly from the original token in the embedding space, leading to incorrect "safe" predictions for harmful content. To exploit this bias in Judge LLMs, we introduce the Emoji Attack -- a method that places emojis within tokens to increase the embedding differences between sub-tokens and their originals. These emojis create new tokens that further distort the token embeddings, exacerbating the bias. To counter the Emoji Attack, we design prompts that help LLMs filter out unusual characters. However, this defense can still be bypassed by using a mix of emojis and other characters. The Emoji Attack can also be combined with existing jailbreaking prompts using few-shot learning, which enables LLMs to generate harmful responses with emojis. These responses are often mistakenly labeled as "safe" by Judge LLMs, allowing the attack to slip through. Our experiments with six state-of-the-art Judge LLMs show that the Emoji Attack allows 25\% of harmful responses to bypass detection by Llama Guard and Llama Guard 2, and up to 75\% by ShieldLM. These results highlight the need for stronger Judge LLMs to address this vulnerability.

Elucidating the Design Choice of Probability Paths in Flow Matching for Forecasting

Flow matching has recently emerged as a powerful paradigm for generative modeling and has been extended to probabilistic time series forecasting in latent spaces. However, the impact of the specific choice of probability path model on forecasting performance remains under-explored. In this work, we demonstrate that forecasting spatio-temporal data with flow matching is highly sensitive to the selection of the probability path model. Motivated by this insight, we propose a novel probability path model designed to improve forecasting performance. Our empirical results across various dynamical system benchmarks show that our model achieves faster convergence during training and improved predictive performance compared to existing probability path models. Importantly, our approach is efficient during inference, requiring only a few sampling steps. This makes our proposed model practical for real-world applications and opens new avenues for probabilistic forecasting.

Tuning Frequency Bias of State Space Models

State space models (SSMs) leverage linear, time-invariant (LTI) systems to effectively learn sequences with long-range dependencies. By analyzing the transfer functions of LTI systems, we find that SSMs exhibit an implicit bias toward capturing low-frequency components more effectively than high-frequency ones. This behavior aligns with the broader notion of frequency bias in deep learning model training. We show that the initialization of an SSM assigns it an innate frequency bias and that training the model in a conventional way does not alter this bias. Based on our theory, we propose two mechanisms to tune frequency bias: either by scaling the initialization to tune the inborn frequency bias; or by applying a Sobolev-norm-based filter to adjust the sensitivity of the gradients to high-frequency inputs, which allows us to change the frequency bias via training. Using an image-denoising task, we empirically show that we can strengthen, weaken, or even reverse the frequency bias using both mechanisms. By tuning the frequency bias, we can also improve SSMs' performance on learning long-range sequences, averaging an 88.26% accuracy on the Long-Range Arena (LRA) benchmark tasks.