Utilizing Image Transforms and Diffusion Models for Generative Modeling of Short and Long Time Series

Lately, there has been a surge in interest surrounding generative modeling of time series data. Most existing approaches are designed either to process short sequences or to handle long-range sequences. This dichotomy can be attributed to gradient issues with recurrent networks, computational costs associated with transformers, and limited expressiveness of state space models. Towards a unified generative model for varying-length time series, we propose in this work to transform sequences into images. By employing invertible transforms such as the delay embedding and the short-time Fourier transform, we unlock three main advantages: i) We can exploit advanced diffusion vision models; ii) We can remarkably process short- and long-range inputs within the same framework; and iii) We can harness recent and established tools proposed in the time series to image literature. We validate the effectiveness of our method through a comprehensive evaluation across multiple tasks, including unconditional generation, interpolation, and extrapolation. We show that our approach achieves consistently state-of-the-art results against strong baselines. In the unconditional generation tasks, we show remarkable mean improvements of 58.17% over previous diffusion models in the short discriminative score and 132.61% in the (ultra-)long classification scores. Code is at https://github.com/azencot-group/ImagenTime.

Learning Physics for Unveiling Hidden Earthquake Ground Motions via Conditional Generative Modeling

Predicting high-fidelity ground motions for future earthquakes is crucial for seismic hazard assessment and infrastructure resilience. Conventional empirical simulations suffer from sparse sensor distribution and geographically localized earthquake locations, while physics-based methods are computationally intensive and require accurate representations of Earth structures and earthquake sources. We propose a novel artificial intelligence (AI) simulator, Conditional Generative Modeling for Ground Motion (CGM-GM), to synthesize high-frequency and spatially continuous earthquake ground motion waveforms. CGM-GM leverages earthquake magnitudes and geographic coordinates of earthquakes and sensors as inputs, learning complex wave physics and Earth heterogeneities, without explicit physics constraints. This is achieved through a probabilistic autoencoder that captures latent distributions in the time-frequency domain and variational sequential models for prior and posterior distributions. We evaluate the performance of CGM-GM using small-magnitude earthquake records from the San Francisco Bay Area, a region with high seismic risks. CGM-GM demonstrates a strong potential for outperforming a state-of-the-art non-ergodic empirical ground motion model and shows great promise in seismology and beyond.

Sequential Disentanglement by Extracting Static Information From A Single Sequence Element

One of the fundamental representation learning tasks is unsupervised sequential disentanglement, where latent codes of inputs are decomposed to a single static factor and a sequence of dynamic factors. To extract this latent information, existing methods condition the static and dynamic codes on the entire input sequence. Unfortunately, these models often suffer from information leakage, i.e., the dynamic vectors encode both static and dynamic information, or vice versa, leading to a non-disentangled representation. Attempts to alleviate this problem via reducing the dynamic dimension and auxiliary loss terms gain only partial success. Instead, we propose a novel and simple architecture that mitigates information leakage by offering a simple and effective subtraction inductive bias while conditioning on a single sample. Remarkably, the resulting variational framework is simpler in terms of required loss terms, hyperparameters, and data augmentation. We evaluate our method on multiple data-modality benchmarks including general time series, video, and audio, and we show beyond state-of-the-art results on generation and prediction tasks in comparison to several strong baselines.

Generative Modeling of Regular and Irregular Time Series Data via Koopman VAEs

Generating realistic time series data is important for many engineering and scientific applications. Existing work tackles this problem using generative adversarial networks (GANs). However, GANs are often unstable during training, and they can suffer from mode collapse. While variational autoencoders (VAEs) are known to be more robust to these issues, they are (surprisingly) less often considered for time series generation. In this work, we introduce Koopman VAE (KVAE), a new generative framework that is based on a novel design for the model prior, and that can be optimized for either regular and irregular training data. Inspired by Koopman theory, we represent the latent conditional prior dynamics using a linear map. Our approach enhances generative modeling with two desired features: (i) incorporating domain knowledge can be achieved by leverageing spectral tools that prescribe constraints on the eigenvalues of the linear map; and (ii) studying the qualitative behavior and stablity of the system can be performed using tools from dynamical systems theory. Our results show that KVAE outperforms state-of-the-art GAN and VAE methods across several challenging synthetic and real-world time series generation benchmarks. Whether trained on regular or irregular data, KVAE generates time series that improve both discriminative and predictive metrics. We also present visual evidence suggesting that KVAE learns probability density functions that better approximate empirical ground truth distributions.

Sample and Predict Your Latent: Modality-free Sequential Disentanglement via Contrastive Estimation

Unsupervised disentanglement is a long-standing challenge in representation learning. Recently, self-supervised techniques achieved impressive results in the sequential setting, where data is time-dependent. However, the latter methods employ modality-based data augmentations and random sampling or solve auxiliary tasks. In this work, we propose to avoid that by generating, sampling, and comparing empirical distributions from the underlying variational model. Unlike existing work, we introduce a self-supervised sequential disentanglement framework based on contrastive estimation with no external signals, while using common batch sizes and samples from the latent space itself. In practice, we propose a unified, efficient, and easy-to-code sampling strategy for semantically similar and dissimilar views of the data. We evaluate our approach on video, audio, and time series benchmarks. Our method presents state-of-the-art results in comparison to existing techniques. The code is available at https://github.com/azencot-group/SPYL.

Multifactor Sequential Disentanglement via Structured Koopman Autoencoders

Disentangling complex data to its latent factors of variation is a fundamental task in representation learning. Existing work on sequential disentanglement mostly provides two factor representations, i.e., it separates the data to time-varying and time-invariant factors. In contrast, we consider multifactor disentanglement in which multiple (more than two) semantic disentangled components are generated. Key to our approach is a strong inductive bias where we assume that the underlying dynamics can be represented linearly in the latent space. Under this assumption, it becomes natural to exploit the recently introduced Koopman autoencoder models. However, disentangled representations are not guaranteed in Koopman approaches, and thus we propose a novel spectral loss term which leads to structured Koopman matrices and disentanglement. Overall, we propose a simple and easy to code new deep model that is fully unsupervised and it supports multifactor disentanglement. We showcase new disentangling abilities such as swapping of individual static factors between characters, and an incremental swap of disentangled factors from the source to the target. Moreover, we evaluate our method extensively on two factor standard benchmark tasks where we significantly improve over competing unsupervised approaches, and we perform competitively in comparison to weakly- and self-supervised state-of-the-art approaches. The code is available at https://github.com/azencot-group/SKD.

A Koopman Approach to Understanding Sequence Neural Models

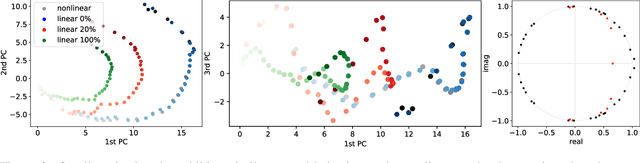
We introduce a new approach to understanding trained sequence neural models: the Koopman Analysis of Neural Networks (KANN) method. Motivated by the relation between time-series models and self-maps, we compute approximate Koopman operators that encode well the latent dynamics. Unlike other existing methods whose applicability is limited, our framework is global, and it has only weak constraints over the inputs. Moreover, the Koopman operator is linear, and it is related to a rich mathematical theory. Thus, we can use tools and insights from linear analysis and Koopman Theory in our study. For instance, we show that the operator eigendecomposition is instrumental in exploring the dominant features of the network. Our results extend across tasks and architectures as we demonstrate for the copy problem, and ECG classification and sentiment analysis tasks.