Annan Yu
HydroDiffusion: Diffusion-Based Probabilistic Streamflow Forecasting with a State Space Backbone
Dec 13, 2025Abstract:Recent advances have introduced diffusion models for probabilistic streamflow forecasting, demonstrating strong early flood-warning skill. However, current implementations rely on recurrent Long Short-Term Memory (LSTM) backbones and single-step training objectives, which limit their ability to capture long-range dependencies and produce coherent forecast trajectories across lead times. To address these limitations, we developed HydroDiffusion, a diffusion-based probabilistic forecasting framework with a decoder-only state space model backbone. The proposed framework jointly denoises full multi-day trajectories in a single pass, ensuring temporal coherence and mitigating error accumulation common in autoregressive prediction. HydroDiffusion is evaluated across 531 watersheds in the contiguous United States (CONUS) in the CAMELS dataset. We benchmark HydroDiffusion against two diffusion baselines with LSTM backbones, as well as the recently proposed Diffusion-based Runoff Model (DRUM). Results show that HydroDiffusion achieves strong nowcast accuracy when driven by observed meteorological forcings, and maintains consistent performance across the full simulation horizon. Moreover, HydroDiffusion delivers stronger deterministic and probabilistic forecast skill than DRUM in operational forecasting. These results establish HydroDiffusion as a robust generative modeling framework for medium-range streamflow forecasting, providing both a new modeling benchmark and a foundation for future research on probabilistic hydrologic prediction at continental scales.
Understanding the Implicit Biases of Design Choices for Time Series Foundation Models
Oct 22, 2025Abstract:Time series foundation models (TSFMs) are a class of potentially powerful, general-purpose tools for time series forecasting and related temporal tasks, but their behavior is strongly shaped by subtle inductive biases in their design. Rather than developing a new model and claiming that it is better than existing TSFMs, e.g., by winning on existing well-established benchmarks, our objective is to understand how the various ``knobs'' of the training process affect model quality. Using a mix of theory and controlled empirical evaluation, we identify several design choices (patch size, embedding choice, training objective, etc.) and show how they lead to implicit biases in fundamental model properties (temporal behavior, geometric structure, how aggressively or not the model regresses to the mean, etc.); and we show how these biases can be intuitive or very counterintuitive, depending on properties of the model and data. We also illustrate in a case study on outlier handling how multiple biases can interact in complex ways; and we discuss implications of our results for learning the bitter lesson and building TSFMs.
Block-Biased Mamba for Long-Range Sequence Processing
May 13, 2025Abstract:Mamba extends earlier state space models (SSMs) by introducing input-dependent dynamics, and has demonstrated strong empirical performance across a range of domains, including language modeling, computer vision, and foundation models. However, a surprising weakness remains: despite being built on architectures designed for long-range dependencies, Mamba performs poorly on long-range sequential tasks. Understanding and addressing this gap is important for improving Mamba's universality and versatility. In this work, we analyze Mamba's limitations through three perspectives: expressiveness, inductive bias, and training stability. Our theoretical results show how Mamba falls short in each of these aspects compared to earlier SSMs such as S4D. To address these issues, we propose $\text{B}_2\text{S}_6$, a simple extension of Mamba's S6 unit that combines block-wise selective dynamics with a channel-specific bias. We prove that these changes equip the model with a better-suited inductive bias and improve its expressiveness and stability. Empirically, $\text{B}_2\text{S}_6$ outperforms S4 and S4D on Long-Range Arena (LRA) tasks while maintaining Mamba's performance on language modeling benchmarks.
A Deep State Space Model for Rainfall-Runoff Simulations
Jan 24, 2025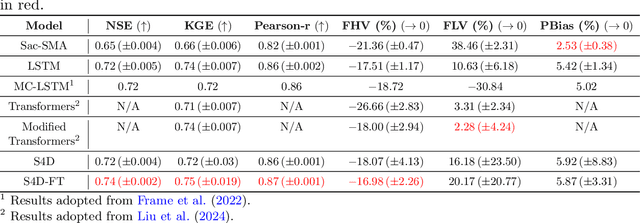

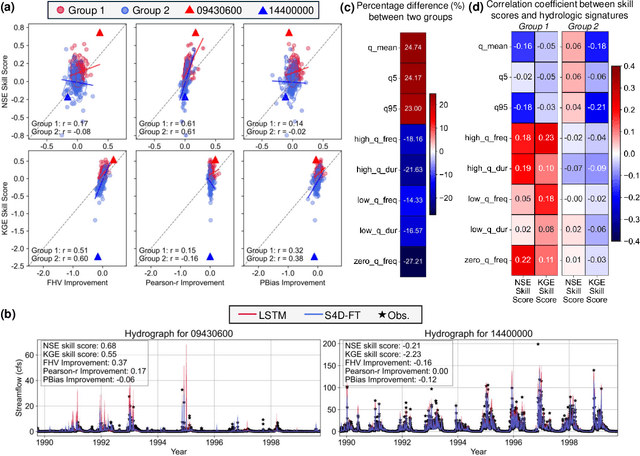
Abstract:The classical way of studying the rainfall-runoff processes in the water cycle relies on conceptual or physically-based hydrologic models. Deep learning (DL) has recently emerged as an alternative and blossomed in hydrology community for rainfall-runoff simulations. However, the decades-old Long Short-Term Memory (LSTM) network remains the benchmark for this task, outperforming newer architectures like Transformers. In this work, we propose a State Space Model (SSM), specifically the Frequency Tuned Diagonal State Space Sequence (S4D-FT) model, for rainfall-runoff simulations. The proposed S4D-FT is benchmarked against the established LSTM and a physically-based Sacramento Soil Moisture Accounting model across 531 watersheds in the contiguous United States (CONUS). Results show that S4D-FT is able to outperform the LSTM model across diverse regions. Our pioneering introduction of the S4D-FT for rainfall-runoff simulations challenges the dominance of LSTM in the hydrology community and expands the arsenal of DL tools available for hydrological modeling.
Elucidating the Design Choice of Probability Paths in Flow Matching for Forecasting
Oct 04, 2024Abstract:Flow matching has recently emerged as a powerful paradigm for generative modeling and has been extended to probabilistic time series forecasting in latent spaces. However, the impact of the specific choice of probability path model on forecasting performance remains under-explored. In this work, we demonstrate that forecasting spatio-temporal data with flow matching is highly sensitive to the selection of the probability path model. Motivated by this insight, we propose a novel probability path model designed to improve forecasting performance. Our empirical results across various dynamical system benchmarks show that our model achieves faster convergence during training and improved predictive performance compared to existing probability path models. Importantly, our approach is efficient during inference, requiring only a few sampling steps. This makes our proposed model practical for real-world applications and opens new avenues for probabilistic forecasting.
Tuning Frequency Bias of State Space Models
Oct 02, 2024



Abstract:State space models (SSMs) leverage linear, time-invariant (LTI) systems to effectively learn sequences with long-range dependencies. By analyzing the transfer functions of LTI systems, we find that SSMs exhibit an implicit bias toward capturing low-frequency components more effectively than high-frequency ones. This behavior aligns with the broader notion of frequency bias in deep learning model training. We show that the initialization of an SSM assigns it an innate frequency bias and that training the model in a conventional way does not alter this bias. Based on our theory, we propose two mechanisms to tune frequency bias: either by scaling the initialization to tune the inborn frequency bias; or by applying a Sobolev-norm-based filter to adjust the sensitivity of the gradients to high-frequency inputs, which allows us to change the frequency bias via training. Using an image-denoising task, we empirically show that we can strengthen, weaken, or even reverse the frequency bias using both mechanisms. By tuning the frequency bias, we can also improve SSMs' performance on learning long-range sequences, averaging an 88.26% accuracy on the Long-Range Arena (LRA) benchmark tasks.
There is HOPE to Avoid HiPPOs for Long-memory State Space Models
May 22, 2024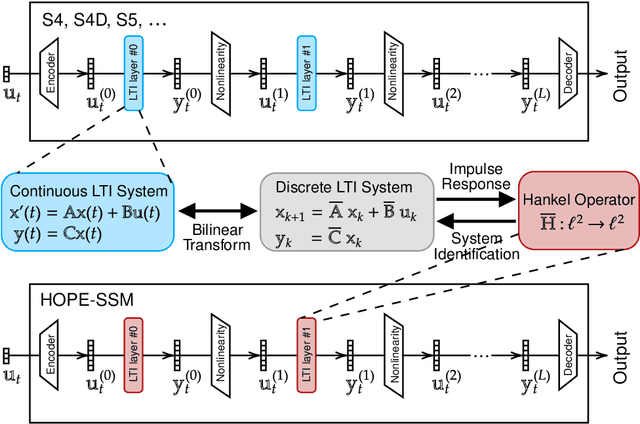
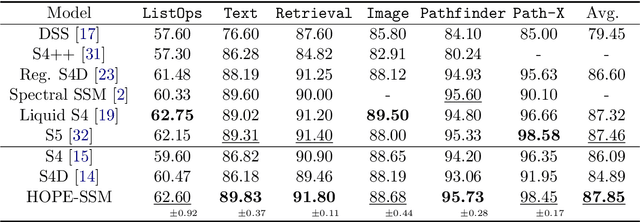
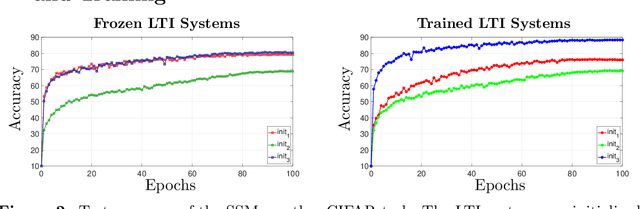
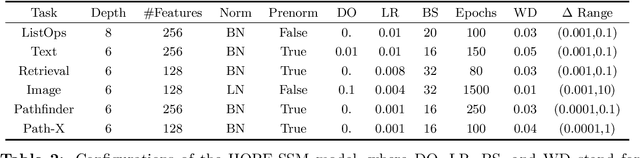
Abstract:State-space models (SSMs) that utilize linear, time-invariant (LTI) systems are known for their effectiveness in learning long sequences. However, these models typically face several challenges: (i) they require specifically designed initializations of the system matrices to achieve state-of-the-art performance, (ii) they require training of state matrices on a logarithmic scale with very small learning rates to prevent instabilities, and (iii) they require the model to have exponentially decaying memory in order to ensure an asymptotically stable LTI system. To address these issues, we view SSMs through the lens of Hankel operator theory, which provides us with a unified theory for the initialization and training of SSMs. Building on this theory, we develop a new parameterization scheme, called HOPE, for LTI systems that utilizes Markov parameters within Hankel operators. This approach allows for random initializations of the LTI systems and helps to improve training stability, while also provides the SSMs with non-decaying memory capabilities. Our model efficiently implements these innovations by nonuniformly sampling the transfer functions of LTI systems, and it requires fewer parameters compared to canonical SSMs. When benchmarked against HiPPO-initialized models such as S4 and S4D, an SSM parameterized by Hankel operators demonstrates improved performance on Long-Range Arena (LRA) tasks. Moreover, we use a sequential CIFAR-10 task with padded noise to empirically corroborate our SSM's long memory capacity.
Robustifying State-space Models for Long Sequences via Approximate Diagonalization
Oct 02, 2023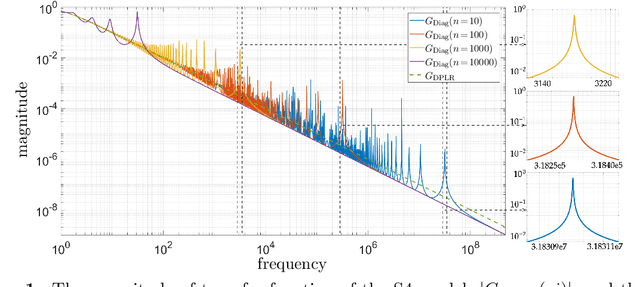
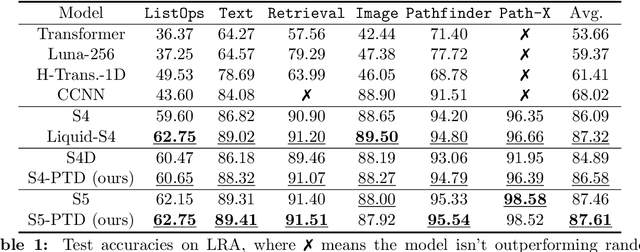
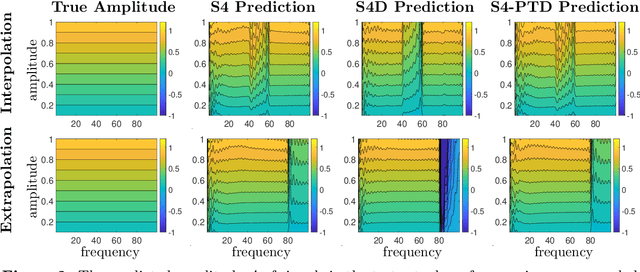
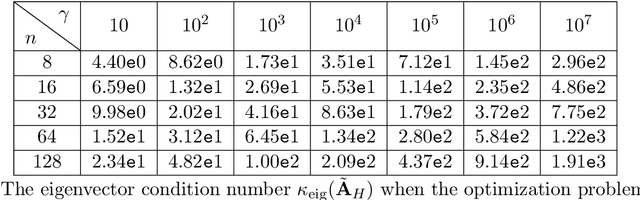
Abstract:State-space models (SSMs) have recently emerged as a framework for learning long-range sequence tasks. An example is the structured state-space sequence (S4) layer, which uses the diagonal-plus-low-rank structure of the HiPPO initialization framework. However, the complicated structure of the S4 layer poses challenges; and, in an effort to address these challenges, models such as S4D and S5 have considered a purely diagonal structure. This choice simplifies the implementation, improves computational efficiency, and allows channel communication. However, diagonalizing the HiPPO framework is itself an ill-posed problem. In this paper, we propose a general solution for this and related ill-posed diagonalization problems in machine learning. We introduce a generic, backward-stable "perturb-then-diagonalize" (PTD) methodology, which is based on the pseudospectral theory of non-normal operators, and which may be interpreted as the approximate diagonalization of the non-normal matrices defining SSMs. Based on this, we introduce the S4-PTD and S5-PTD models. Through theoretical analysis of the transfer functions of different initialization schemes, we demonstrate that the S4-PTD/S5-PTD initialization strongly converges to the HiPPO framework, while the S4D/S5 initialization only achieves weak convergences. As a result, our new models show resilience to Fourier-mode noise-perturbed inputs, a crucial property not achieved by the S4D/S5 models. In addition to improved robustness, our S5-PTD model averages 87.6% accuracy on the Long-Range Arena benchmark, demonstrating that the PTD methodology helps to improve the accuracy of deep learning models.
A Quadrature Perspective on Frequency Bias in Neural Network Training with Nonuniform Data
May 28, 2022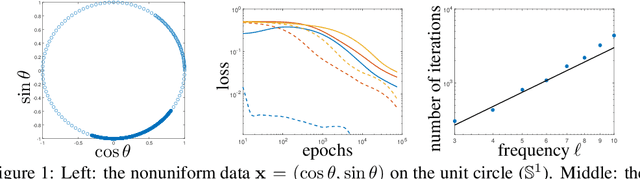
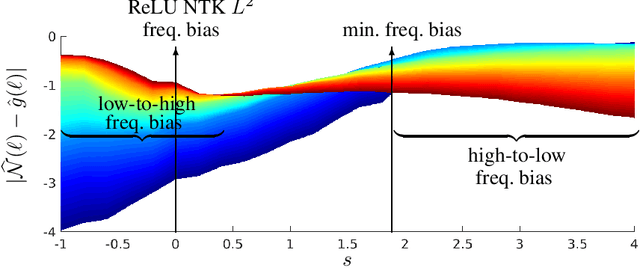


Abstract:Small generalization errors of over-parameterized neural networks (NNs) can be partially explained by the frequency biasing phenomenon, where gradient-based algorithms minimize the low-frequency misfit before reducing the high-frequency residuals. Using the Neural Tangent Kernel (NTK), one can provide a theoretically rigorous analysis for training where data are drawn from constant or piecewise-constant probability densities. Since most training data sets are not drawn from such distributions, we use the NTK model and a data-dependent quadrature rule to theoretically quantify the frequency biasing of NN training given fully nonuniform data. By replacing the loss function with a carefully selected Sobolev norm, we can further amplify, dampen, counterbalance, or reverse the intrinsic frequency biasing in NN training.
Arbitrary-Depth Universal Approximation Theorems for Operator Neural Networks
Sep 23, 2021
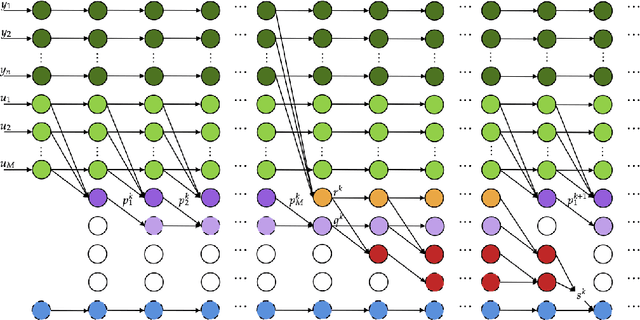
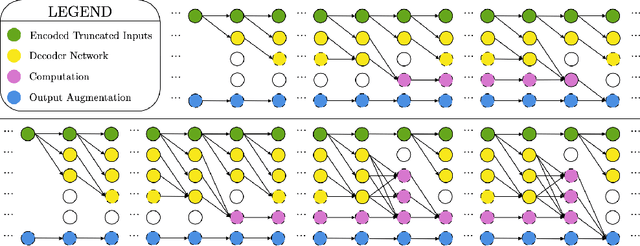
Abstract:The standard Universal Approximation Theorem for operator neural networks (NNs) holds for arbitrary width and bounded depth. Here, we prove that operator NNs of bounded width and arbitrary depth are universal approximators for continuous nonlinear operators. In our main result, we prove that for non-polynomial activation functions that are continuously differentiable at a point with a nonzero derivative, one can construct an operator NN of width five, whose inputs are real numbers with finite decimal representations, that is arbitrarily close to any given continuous nonlinear operator. We derive an analogous result for non-affine polynomial activation functions. We also show that depth has theoretical advantages by constructing operator ReLU NNs of depth $2k^3+8$ and constant width that cannot be well-approximated by any operator ReLU NN of depth $k$, unless its width is exponential in $k$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge