Invariant Measures in Time-Delay Coordinates for Unique Dynamical System Identification

Invariant measures are widely used to compare chaotic dynamical systems, as they offer robustness to noisy data, uncertain initial conditions, and irregular sampling. However, large classes of systems with distinct transient dynamics can still exhibit the same asymptotic statistical behavior, which poses challenges when invariant measures alone are used to perform system identification. Motivated by Takens' seminal embedding theory, we propose studying invariant measures in time-delay coordinates, which exhibit enhanced sensitivity to the underlying dynamics. Our first result demonstrates that a single invariant measure in time-delay coordinates can be used to perform system identification up to a topological conjugacy. This result already surpasses the capabilities of invariant measures in the original state coordinate. Continuing to explore the power of delay-coordinates, we eliminate all ambiguity from the conjugacy relation by showing that unique system identification can be achieved using additional invariant measures in time-delay coordinates constructed from different observables. Our findings improve the effectiveness of invariant measures in system identification and broaden the scope of measure-theoretic approaches to modeling dynamical systems.

Sampling with Adaptive Variance for Multimodal Distributions

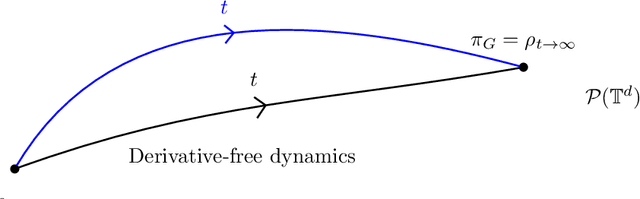
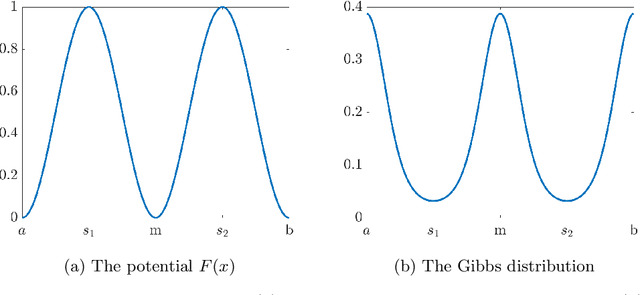
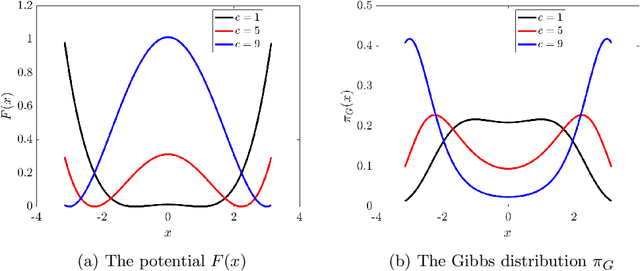
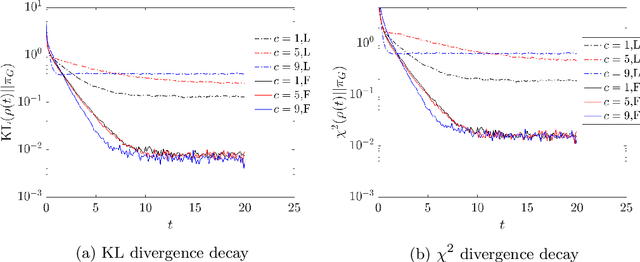
We propose and analyze a class of adaptive sampling algorithms for multimodal distributions on a bounded domain, which share a structural resemblance to the classic overdamped Langevin dynamics. We first demonstrate that this class of linear dynamics with adaptive diffusion coefficients and vector fields can be interpreted and analyzed as weighted Wasserstein gradient flows of the Kullback--Leibler (KL) divergence between the current distribution and the target Gibbs distribution, which directly leads to the exponential convergence of both the KL and $\chi^2$ divergences, with rates depending on the weighted Wasserstein metric and the Gibbs potential. We then show that a derivative-free version of the dynamics can be used for sampling without gradient information of the Gibbs potential and that for Gibbs distributions with nonconvex potentials, this approach could achieve significantly faster convergence than the classical overdamped Langevin dynamics. A comparison of the mean transition times between local minima of a nonconvex potential further highlights the better efficiency of the derivative-free dynamics in sampling.

Measure-Theoretic Time-Delay Embedding

The celebrated Takens' embedding theorem provides a theoretical foundation for reconstructing the full state of a dynamical system from partial observations. However, the classical theorem assumes that the underlying system is deterministic and that observations are noise-free, limiting its applicability in real-world scenarios. Motivated by these limitations, we rigorously establish a measure-theoretic generalization that adopts an Eulerian description of the dynamics and recasts the embedding as a pushforward map between probability spaces. Our mathematical results leverage recent advances in optimal transportation theory. Building on our novel measure-theoretic time-delay embedding theory, we have developed a new computational framework that forecasts the full state of a dynamical system from time-lagged partial observations, engineered with better robustness to handle sparse and noisy data. We showcase the efficacy and versatility of our approach through several numerical examples, ranging from the classic Lorenz-63 system to large-scale, real-world applications such as NOAA sea surface temperature forecasting and ERA5 wind field reconstruction.

Generative Modeling of Time-Dependent Densities via Optimal Transport and Projection Pursuit

Motivated by the computational difficulties incurred by popular deep learning algorithms for the generative modeling of temporal densities, we propose a cheap alternative which requires minimal hyperparameter tuning and scales favorably to high dimensional problems. In particular, we use a projection-based optimal transport solver [Meng et al., 2019] to join successive samples and subsequently use transport splines [Chewi et al., 2020] to interpolate the evolving density. When the sampling frequency is sufficiently high, the optimal maps are close to the identity and are thus computationally efficient to compute. Moreover, the training process is highly parallelizable as all optimal maps are independent and can thus be learned simultaneously. Finally, the approach is based solely on numerical linear algebra rather than minimizing a nonconvex objective function, allowing us to easily analyze and control the algorithm. We present several numerical experiments on both synthetic and real-world datasets to demonstrate the efficiency of our method. In particular, these experiments show that the proposed approach is highly competitive compared with state-of-the-art normalizing flows conditioned on time across a wide range of dimensionalities.

Adaptive State-Dependent Diffusion for Derivative-Free Optimization

This paper develops and analyzes a stochastic derivative-free optimization strategy. A key feature is the state-dependent adaptive variance. We prove global convergence in probability with algebraic rate and give the quantitative results in numerical examples. A striking fact is that convergence is achieved without explicit information of the gradient and even without comparing different objective function values as in established methods such as the simplex method and simulated annealing. It can otherwise be compared to annealing with state-dependent temperature.

Neural Inverse Operators for Solving PDE Inverse Problems

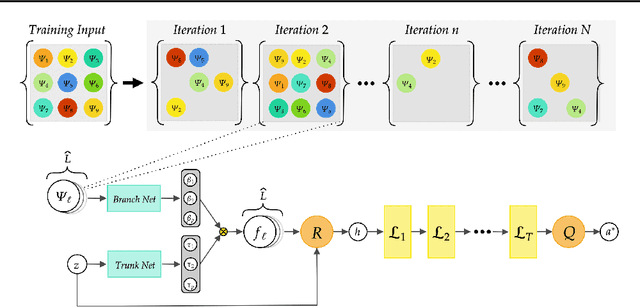
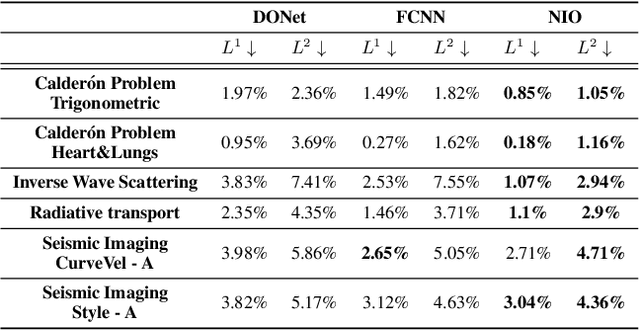
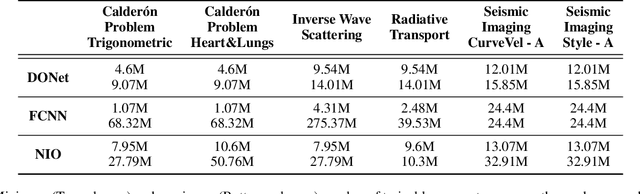
A large class of inverse problems for PDEs are only well-defined as mappings from operators to functions. Existing operator learning frameworks map functions to functions and need to be modified to learn inverse maps from data. We propose a novel architecture termed Neural Inverse Operators (NIOs) to solve these PDE inverse problems. Motivated by the underlying mathematical structure, NIO is based on a suitable composition of DeepONets and FNOs to approximate mappings from operators to functions. A variety of experiments are presented to demonstrate that NIOs significantly outperform baselines and solve PDE inverse problems robustly, accurately and are several orders of magnitude faster than existing direct and PDE-constrained optimization methods.

A Quadrature Perspective on Frequency Bias in Neural Network Training with Nonuniform Data

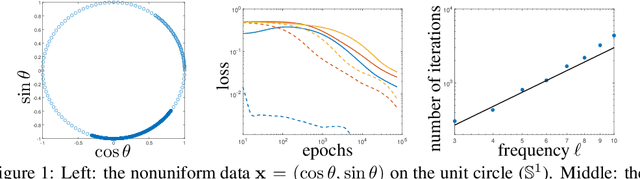
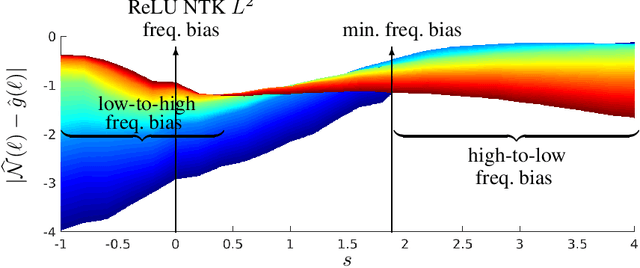
Small generalization errors of over-parameterized neural networks (NNs) can be partially explained by the frequency biasing phenomenon, where gradient-based algorithms minimize the low-frequency misfit before reducing the high-frequency residuals. Using the Neural Tangent Kernel (NTK), one can provide a theoretically rigorous analysis for training where data are drawn from constant or piecewise-constant probability densities. Since most training data sets are not drawn from such distributions, we use the NTK model and a data-dependent quadrature rule to theoretically quantify the frequency biasing of NN training given fully nonuniform data. By replacing the loss function with a carefully selected Sobolev norm, we can further amplify, dampen, counterbalance, or reverse the intrinsic frequency biasing in NN training.

An Algebraically Converging Stochastic Gradient Descent Algorithm for Global Optimization

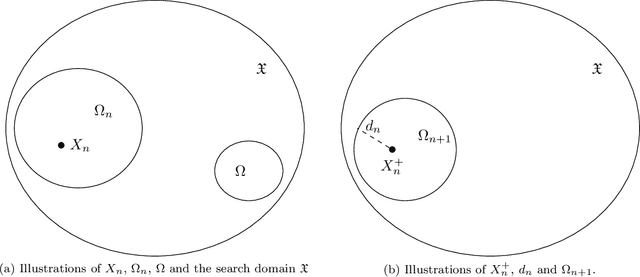
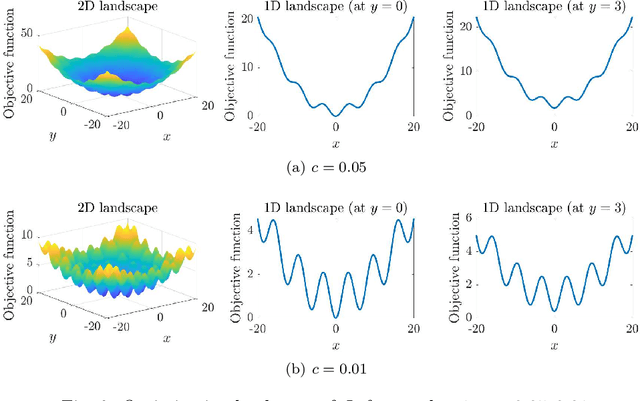
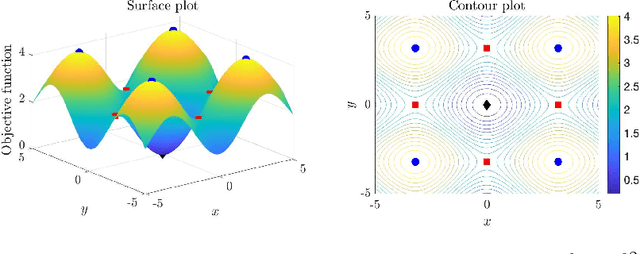
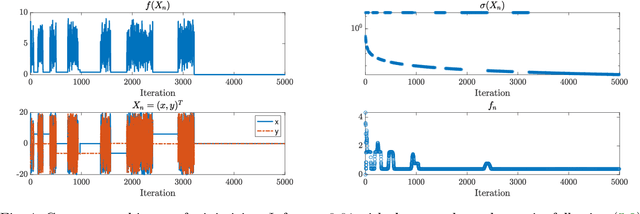
We propose a new stochastic gradient descent algorithm for finding the global optimizer of nonconvex optimization problems, referred to here as "AdaVar". A key component in the algorithm is the adaptive tuning of the randomness based on the value of the objective function. In the language of simulated annealing, the temperature is state-dependent. With this, we can prove global convergence with an algebraic rate both in probability and in the parameter space. This is a major improvement over the classical rate from using a simpler control of the noise term. The convergence proof is based on the actual discrete setup of the algorithm. We also present several numerical examples demonstrating the efficiency and robustness of the algorithm for global convergence.

Efficient Natural Gradient Descent Methods for Large-Scale Optimization Problems

We propose an efficient numerical method for computing natural gradient descent directions with respect to a generic metric in the state space. Our technique relies on representing the natural gradient direction as a solution to a standard least-squares problem. Hence, instead of calculating, storing, or inverting the information matrix directly, we apply efficient methods from numerical linear algebra to solve this least-squares problem. We treat both scenarios where the derivative of the state variable with respect to the parameter is either explicitly known or implicitly given through constraints. We apply the QR decomposition to solve the least-squares problem in the former case and utilize the adjoint-state method to compute the natural gradient descent direction in the latter case. As a result, we can reliably compute several natural gradient descents, including the Wasserstein natural gradient, for a large-scale parameter space with thousands of dimensions, which was believed to be out of reach. Finally, our numerical results shed light on the qualitative differences among the standard gradient descent method and various natural gradient descent methods based on different metric spaces in large-scale nonconvex optimization problems.

A Generalized Weighted Optimization Method for Computational Learning and Inversion

The generalization capacity of various machine learning models exhibits different phenomena in the under- and over-parameterized regimes. In this paper, we focus on regression models such as feature regression and kernel regression and analyze a generalized weighted least-squares optimization method for computational learning and inversion with noisy data. The highlight of the proposed framework is that we allow weighting in both the parameter space and the data space. The weighting scheme encodes both a priori knowledge on the object to be learned and a strategy to weight the contribution of different data points in the loss function. Here, we characterize the impact of the weighting scheme on the generalization error of the learning method, where we derive explicit generalization errors for the random Fourier feature model in both the under- and over-parameterized regimes. For more general feature maps, error bounds are provided based on the singular values of the feature matrix. We demonstrate that appropriate weighting from prior knowledge can improve the generalization capability of the learned model.