Sampling with Adaptive Variance for Multimodal Distributions
Paper and Code
Nov 20, 2024
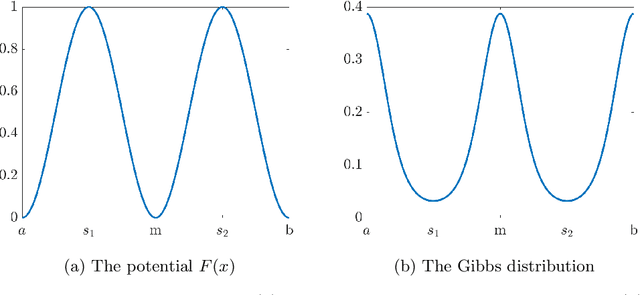
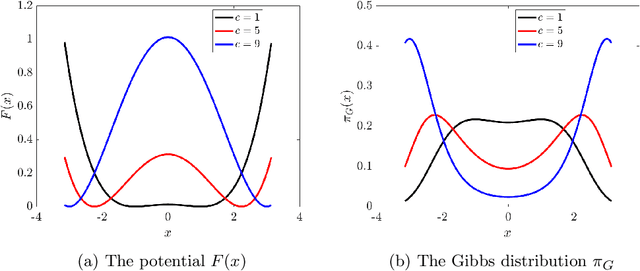
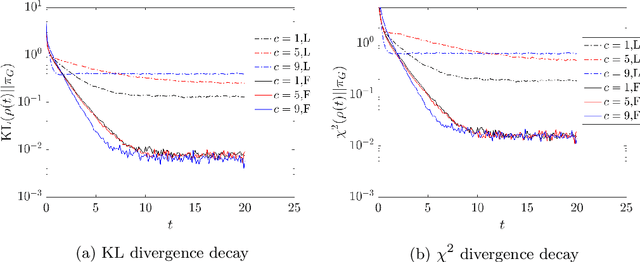
We propose and analyze a class of adaptive sampling algorithms for multimodal distributions on a bounded domain, which share a structural resemblance to the classic overdamped Langevin dynamics. We first demonstrate that this class of linear dynamics with adaptive diffusion coefficients and vector fields can be interpreted and analyzed as weighted Wasserstein gradient flows of the Kullback--Leibler (KL) divergence between the current distribution and the target Gibbs distribution, which directly leads to the exponential convergence of both the KL and $\chi^2$ divergences, with rates depending on the weighted Wasserstein metric and the Gibbs potential. We then show that a derivative-free version of the dynamics can be used for sampling without gradient information of the Gibbs potential and that for Gibbs distributions with nonconvex potentials, this approach could achieve significantly faster convergence than the classical overdamped Langevin dynamics. A comparison of the mean transition times between local minima of a nonconvex potential further highlights the better efficiency of the derivative-free dynamics in sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge