Sampling with Adaptive Variance for Multimodal Distributions

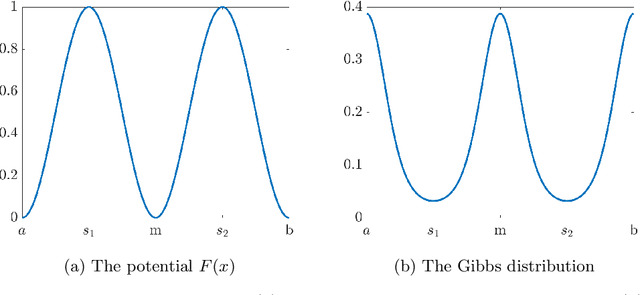
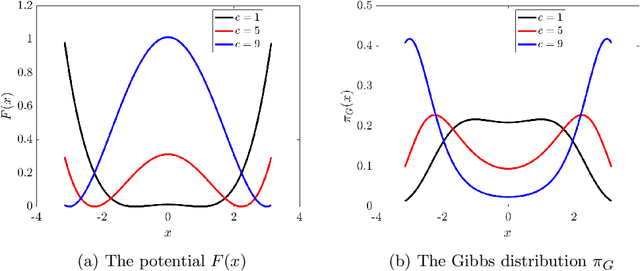
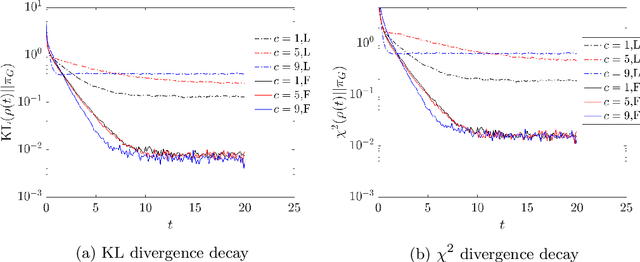
We propose and analyze a class of adaptive sampling algorithms for multimodal distributions on a bounded domain, which share a structural resemblance to the classic overdamped Langevin dynamics. We first demonstrate that this class of linear dynamics with adaptive diffusion coefficients and vector fields can be interpreted and analyzed as weighted Wasserstein gradient flows of the Kullback--Leibler (KL) divergence between the current distribution and the target Gibbs distribution, which directly leads to the exponential convergence of both the KL and $\chi^2$ divergences, with rates depending on the weighted Wasserstein metric and the Gibbs potential. We then show that a derivative-free version of the dynamics can be used for sampling without gradient information of the Gibbs potential and that for Gibbs distributions with nonconvex potentials, this approach could achieve significantly faster convergence than the classical overdamped Langevin dynamics. A comparison of the mean transition times between local minima of a nonconvex potential further highlights the better efficiency of the derivative-free dynamics in sampling.

Adaptive State-Dependent Diffusion for Derivative-Free Optimization

This paper develops and analyzes a stochastic derivative-free optimization strategy. A key feature is the state-dependent adaptive variance. We prove global convergence in probability with algebraic rate and give the quantitative results in numerical examples. A striking fact is that convergence is achieved without explicit information of the gradient and even without comparing different objective function values as in established methods such as the simplex method and simulated annealing. It can otherwise be compared to annealing with state-dependent temperature.

Neural Inverse Operators for Solving PDE Inverse Problems

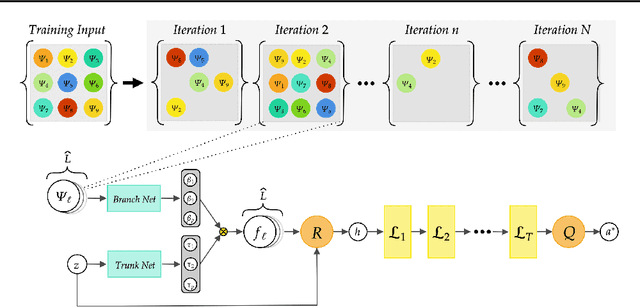
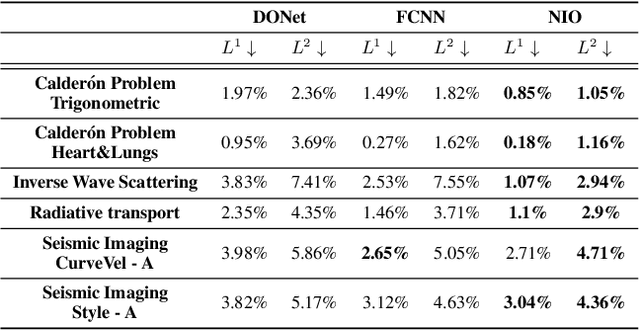
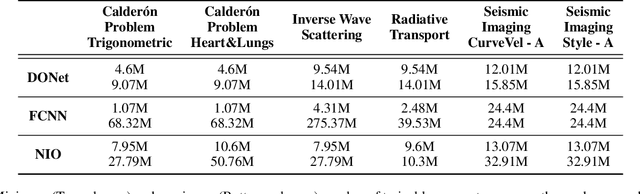
A large class of inverse problems for PDEs are only well-defined as mappings from operators to functions. Existing operator learning frameworks map functions to functions and need to be modified to learn inverse maps from data. We propose a novel architecture termed Neural Inverse Operators (NIOs) to solve these PDE inverse problems. Motivated by the underlying mathematical structure, NIO is based on a suitable composition of DeepONets and FNOs to approximate mappings from operators to functions. A variety of experiments are presented to demonstrate that NIOs significantly outperform baselines and solve PDE inverse problems robustly, accurately and are several orders of magnitude faster than existing direct and PDE-constrained optimization methods.

An Algebraically Converging Stochastic Gradient Descent Algorithm for Global Optimization

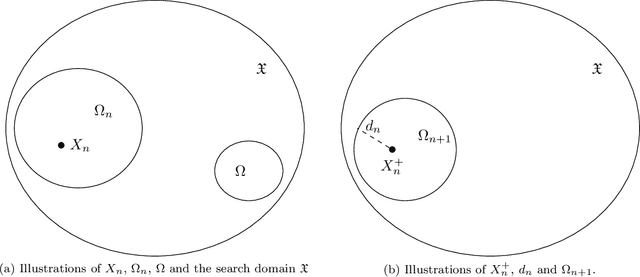
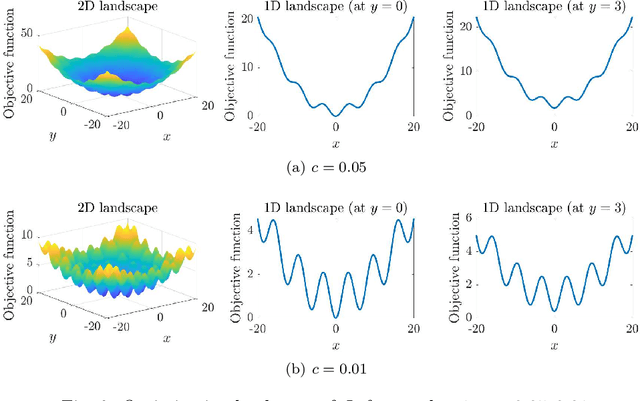
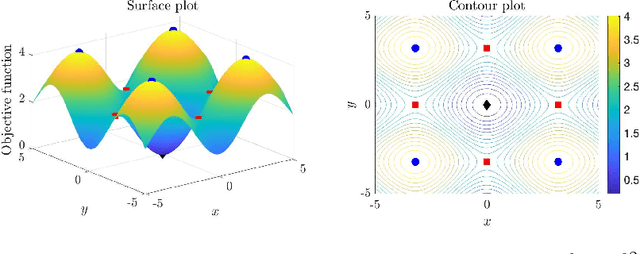
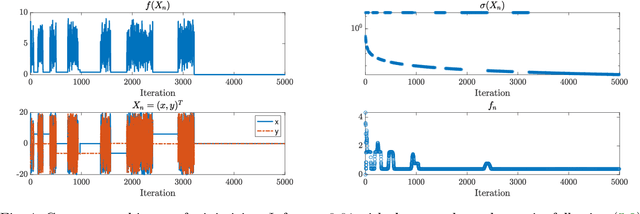
We propose a new stochastic gradient descent algorithm for finding the global optimizer of nonconvex optimization problems, referred to here as "AdaVar". A key component in the algorithm is the adaptive tuning of the randomness based on the value of the objective function. In the language of simulated annealing, the temperature is state-dependent. With this, we can prove global convergence with an algebraic rate both in probability and in the parameter space. This is a major improvement over the classical rate from using a simpler control of the noise term. The convergence proof is based on the actual discrete setup of the algorithm. We also present several numerical examples demonstrating the efficiency and robustness of the algorithm for global convergence.

A Generalized Weighted Optimization Method for Computational Learning and Inversion

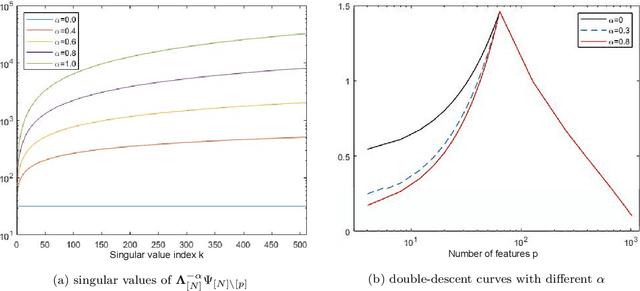
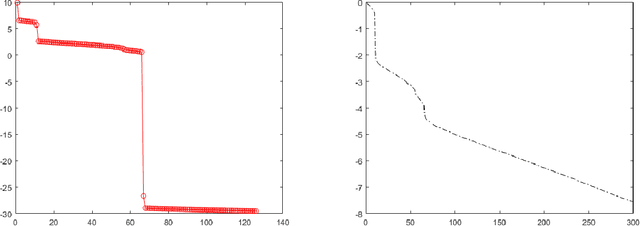
The generalization capacity of various machine learning models exhibits different phenomena in the under- and over-parameterized regimes. In this paper, we focus on regression models such as feature regression and kernel regression and analyze a generalized weighted least-squares optimization method for computational learning and inversion with noisy data. The highlight of the proposed framework is that we allow weighting in both the parameter space and the data space. The weighting scheme encodes both a priori knowledge on the object to be learned and a strategy to weight the contribution of different data points in the loss function. Here, we characterize the impact of the weighting scheme on the generalization error of the learning method, where we derive explicit generalization errors for the random Fourier feature model in both the under- and over-parameterized regimes. For more general feature maps, error bounds are provided based on the singular values of the feature matrix. We demonstrate that appropriate weighting from prior knowledge can improve the generalization capability of the learned model.