Measure-Theoretic Time-Delay Embedding

The celebrated Takens' embedding theorem provides a theoretical foundation for reconstructing the full state of a dynamical system from partial observations. However, the classical theorem assumes that the underlying system is deterministic and that observations are noise-free, limiting its applicability in real-world scenarios. Motivated by these limitations, we rigorously establish a measure-theoretic generalization that adopts an Eulerian description of the dynamics and recasts the embedding as a pushforward map between probability spaces. Our mathematical results leverage recent advances in optimal transportation theory. Building on our novel measure-theoretic time-delay embedding theory, we have developed a new computational framework that forecasts the full state of a dynamical system from time-lagged partial observations, engineered with better robustness to handle sparse and noisy data. We showcase the efficacy and versatility of our approach through several numerical examples, ranging from the classic Lorenz-63 system to large-scale, real-world applications such as NOAA sea surface temperature forecasting and ERA5 wind field reconstruction.

Learning the Delay Using Neural Delay Differential Equations

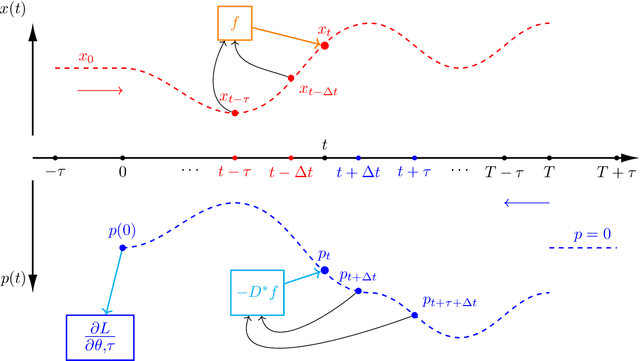
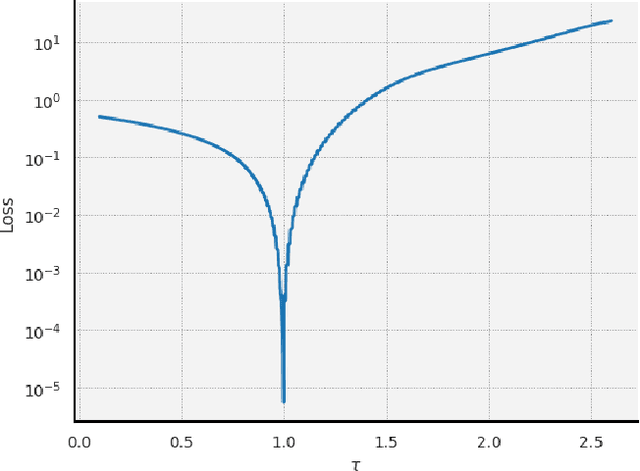
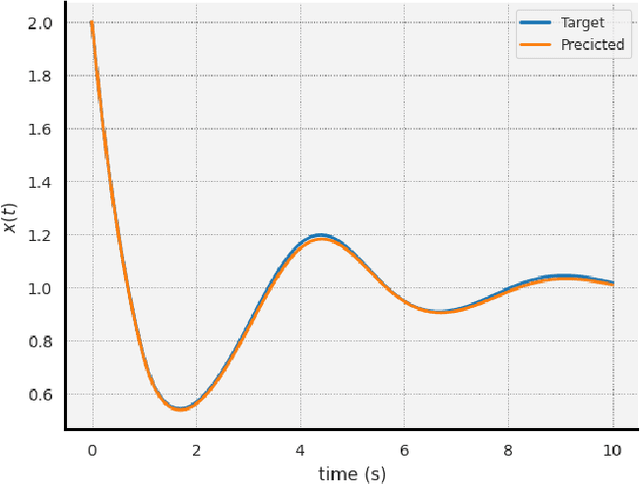
The intersection of machine learning and dynamical systems has generated considerable interest recently. Neural Ordinary Differential Equations (NODEs) represent a rich overlap between these fields. In this paper, we develop a continuous time neural network approach based on Delay Differential Equations (DDEs). Our model uses the adjoint sensitivity method to learn the model parameters and delay directly from data. Our approach is inspired by that of NODEs and extends earlier neural DDE models, which have assumed that the value of the delay is known a priori. We perform a sensitivity analysis on our proposed approach and demonstrate its ability to learn DDE parameters from benchmark systems. We conclude our discussion with potential future directions and applications.