Learning the Delay Using Neural Delay Differential Equations
Paper and Code
Apr 03, 2023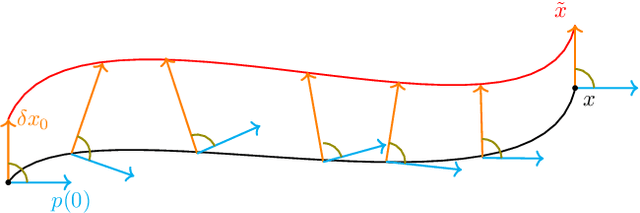
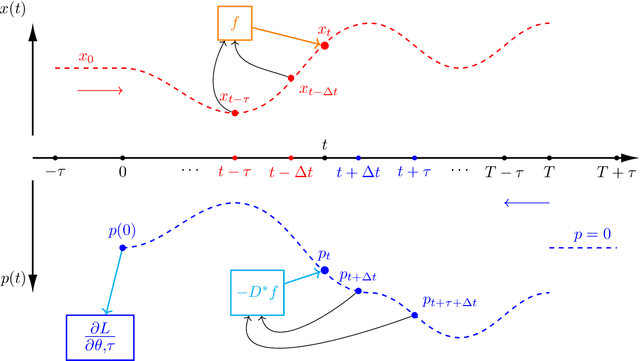
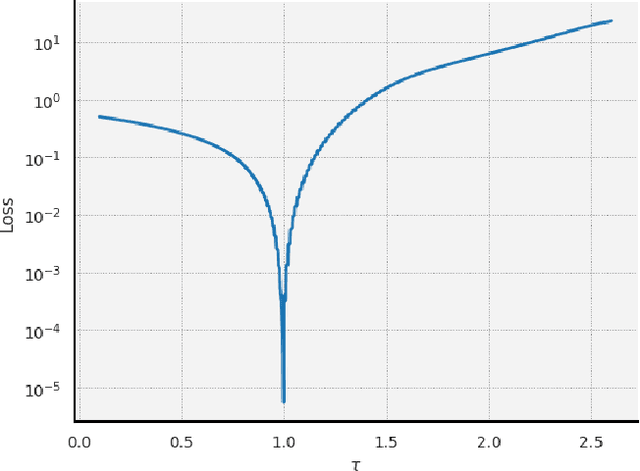
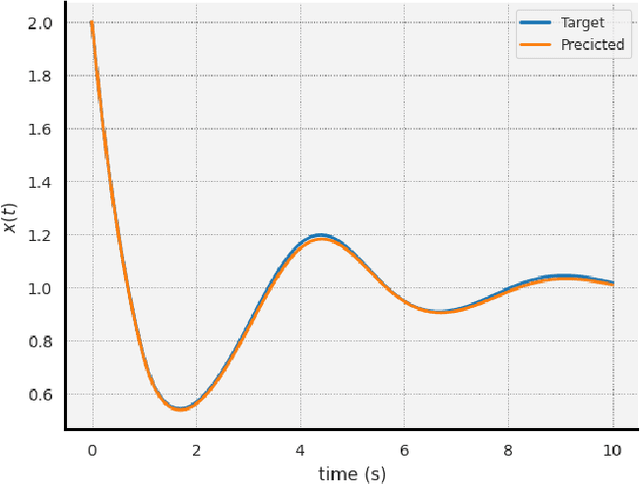
The intersection of machine learning and dynamical systems has generated considerable interest recently. Neural Ordinary Differential Equations (NODEs) represent a rich overlap between these fields. In this paper, we develop a continuous time neural network approach based on Delay Differential Equations (DDEs). Our model uses the adjoint sensitivity method to learn the model parameters and delay directly from data. Our approach is inspired by that of NODEs and extends earlier neural DDE models, which have assumed that the value of the delay is known a priori. We perform a sensitivity analysis on our proposed approach and demonstrate its ability to learn DDE parameters from benchmark systems. We conclude our discussion with potential future directions and applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge