Deep Learning for Low-Latency, Quantum-Ready RF Sensing

Recent work has shown the promise of applying deep learning to enhance software processing of radio frequency (RF) signals. In parallel, hardware developments with quantum RF sensors based on Rydberg atoms are breaking longstanding barriers in frequency range, resolution, and sensitivity. In this paper, we describe our implementations of quantum-ready machine learning approaches for RF signal classification. Our primary objective is latency: while deep learning offers a more powerful computational paradigm, it also traditionally incurs latency overheads that hinder wider scale deployment. Our work spans three axes. (1) A novel continuous wavelet transform (CWT) based recurrent neural network (RNN) architecture that enables flexible online classification of RF signals on-the-fly with reduced sampling time. (2) Low-latency inference techniques for both GPU and CPU that span over 100x reductions in inference time, enabling real-time operation with sub-millisecond inference. (3) Quantum-readiness validated through application of our models to physics-based simulation of Rydberg atom QRF sensors. Altogether, our work bridges towards next-generation RF sensors that use quantum technology to surpass previous physical limits, paired with latency-optimized AI/ML software that is suitable for real-time deployment.

The Interplay Between Symmetries and Impact Effects on Hybrid Mechanical Systems

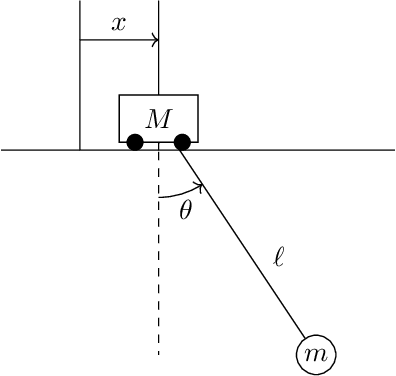
Hybrid systems are dynamical systems with continuous-time and discrete-time components in their dynamics. When hybrid systems are defined on a principal bundle we are able to define two classes of impacts for the discrete-time transition of the dynamics: interior impacts and exterior impacts. In this paper we define hybrid systems on principal bundles, study the underlying geometry on the switching surface where impacts occur and we find conditions for which both exterior and interior impacts are preserved by the mechanical connection induced in the principal bundle.

Learning the Delay Using Neural Delay Differential Equations

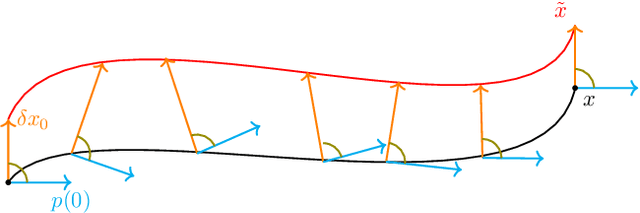
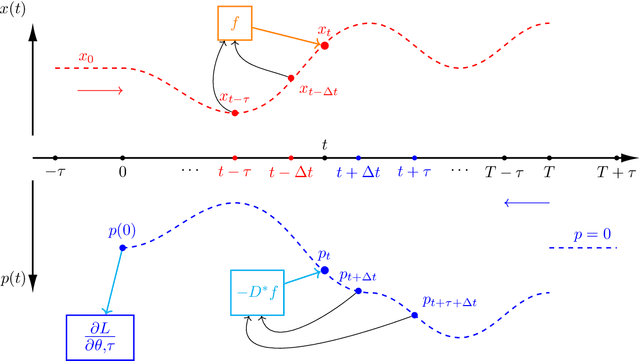
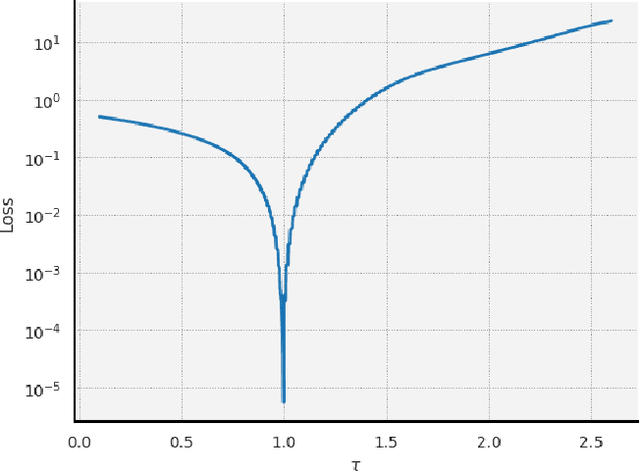
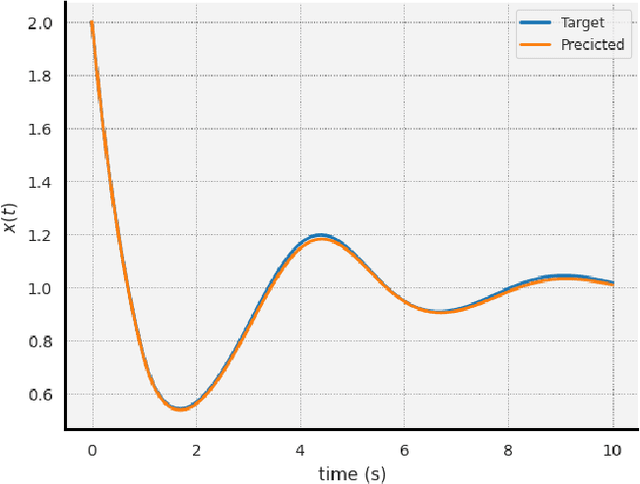
The intersection of machine learning and dynamical systems has generated considerable interest recently. Neural Ordinary Differential Equations (NODEs) represent a rich overlap between these fields. In this paper, we develop a continuous time neural network approach based on Delay Differential Equations (DDEs). Our model uses the adjoint sensitivity method to learn the model parameters and delay directly from data. Our approach is inspired by that of NODEs and extends earlier neural DDE models, which have assumed that the value of the delay is known a priori. We perform a sensitivity analysis on our proposed approach and demonstrate its ability to learn DDE parameters from benchmark systems. We conclude our discussion with potential future directions and applications.

Lie Algebraic Cost Function Design for Control on Lie Groups

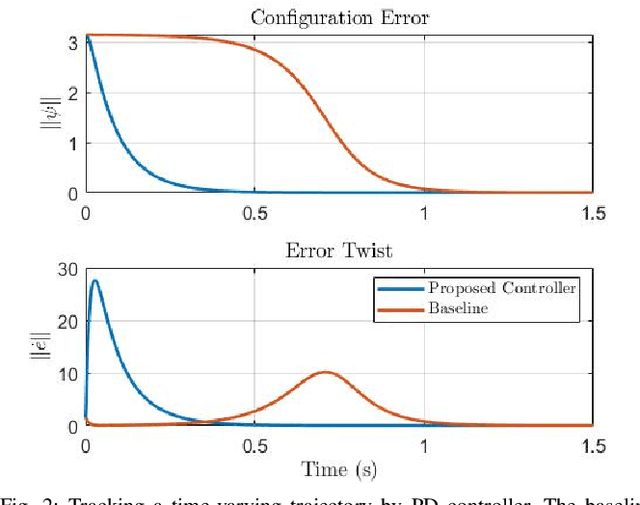
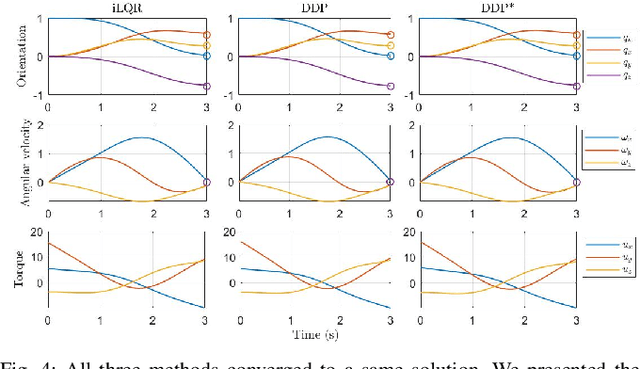
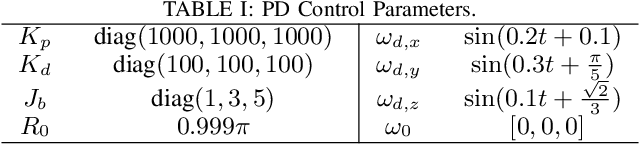
This paper presents a control framework on Lie groups by designing the control objective in its Lie algebra. Control on Lie groups is challenging due to its nonlinear nature and difficulties in system parameterization. Existing methods to design the control objective on a Lie group and then derive the gradient for controller design are non-trivial and can result in slow convergence in tracking control. We show that with a proper left-invariant metric, setting the gradient of the cost function as the tracking error in the Lie algebra leads to a quadratic Lyapunov function that enables globally exponential convergence. In the PD control case, we show that our controller can maintain an exponential convergence rate even when the initial error is approaching $\pi$ in SO(3). We also show the merit of this proposed framework in trajectory optimization. The proposed cost function enables the iterative Linear Quadratic Regulator (iLQR) to converge much faster than the Differential Dynamic Programming (DDP) with a well-adopted cost function when the initial trajectory is poorly initialized on SO(3).

An Error-State Model Predictive Control on Connected Matrix Lie Groups for Legged Robot Control

This paper reports on a new error-state Model Predictive Control (MPC) approach on connected matrix Lie groups for robot control. The linearized tracking error dynamics and the linearized equations of motion are derived in the Lie algebra. Moreover, given an initial condition, the linearized tracking error dynamics and equations of motion are globally valid and evolve independently of the system trajectory. By exploiting the symmetry of the problem, the proposed approach shows faster convergence of rotation and position simultaneously than the state-of-the-art geometric variational MPC based on variational-based linearization. Numerical simulation on tracking control of a fully-actuated 3D rigid body dynamics confirms the benefits of the proposed approach compared to the baselines. Furthermore, the proposed MPC is also verified in pose control and locomotion experiments on a quadrupedal robot MIT Mini Cheetah.

Optimal Target Shape for LiDAR Pose Estimation

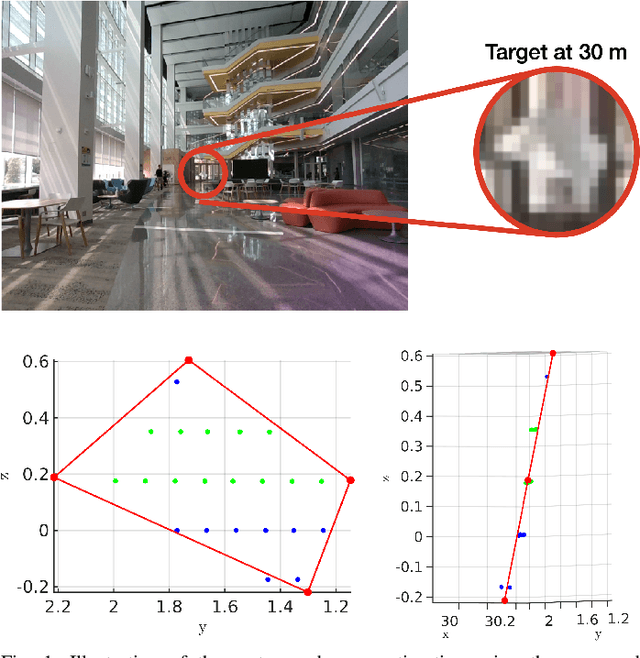
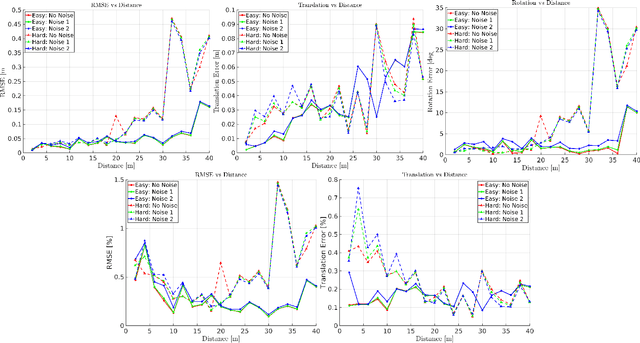
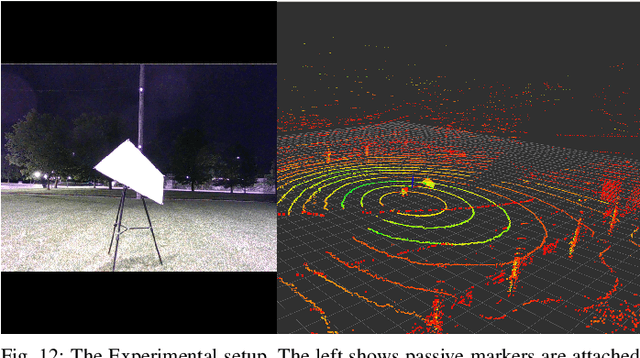
Targets are essential in problems such as object tracking in cluttered or textureless environments, camera (and multi-sensor) calibration tasks, and simultaneous localization and mapping (SLAM). Target shapes for these tasks typically are symmetric (square, rectangular, or circular) and work well for structured, dense sensor data such as pixel arrays (i.e., image). However, symmetric shapes lead to pose ambiguity when using sparse sensor data such as LiDAR point clouds and suffer from the quantization uncertainty of the LiDAR. This paper introduces the concept of optimizing target shape to remove pose ambiguity for LiDAR point clouds. A target is designed to induce large gradients at edge points under rotation and translation relative to the LiDAR to ameliorate the quantization uncertainty associated with point cloud sparseness. Moreover, given a target shape, we present a means that leverages the target's geometry to estimate the target's vertices while globally estimating the pose. Both the simulation and the experimental results (verified by a motion capture system) confirm that by using the optimal shape and the global solver, we achieve centimeter error in translation and a few degrees in rotation even when a partially illuminated target is placed 30 meters away. All the implementations and datasets are available at https://github.com/UMich-BipedLab/optimal_shape_global_pose_estimation.

Asymmetric Private Set Intersection with Applications to Contact Tracing and Private Vertical Federated Machine Learning

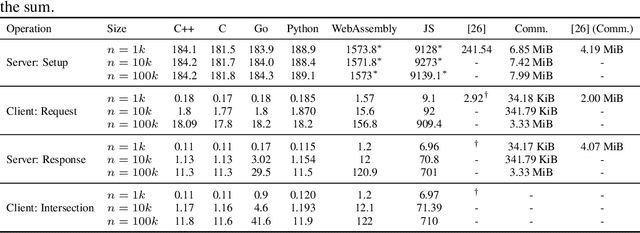
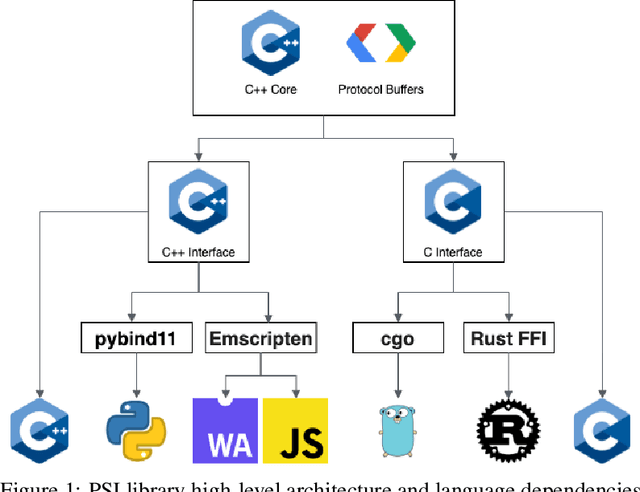
We present a multi-language, cross-platform, open-source library for asymmetric private set intersection (PSI) and PSI-Cardinality (PSI-C). Our protocol combines traditional DDH-based PSI and PSI-C protocols with compression based on Bloom filters that helps reduce communication in the asymmetric setting. Currently, our library supports C++, C, Go, WebAssembly, JavaScript, Python, and Rust, and runs on both traditional hardware (x86) and browser targets. We further apply our library to two use cases: (i) a privacy-preserving contact tracing protocol that is compatible with existing approaches, but improves their privacy guarantees, and (ii) privacy-preserving machine learning on vertically partitioned data.

A Path-Dependent Variational Framework for Incremental Information Gathering

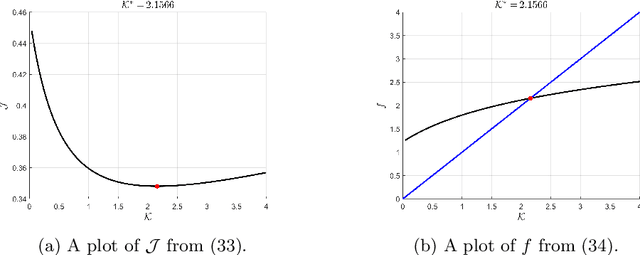
Information gathered along a path is inherently submodular; the incremental amount of information gained along a path decreases due to redundant observations. In addition to submodularity, the incremental amount of information gained is a function of not only the current state but also the entire history as well. This paper presents the construction of the first-order necessary optimality conditions for memory (history-dependent) Lagrangians. Path-dependent problems frequently appear in robotics and artificial intelligence, where the state such as a map is partially observable, and information can only be obtained along a trajectory by local sensing. Robotic exploration and environmental monitoring has numerous real-world applications and can be formulated using the proposed approach.

Nonparametric Continuous Sensor Registration

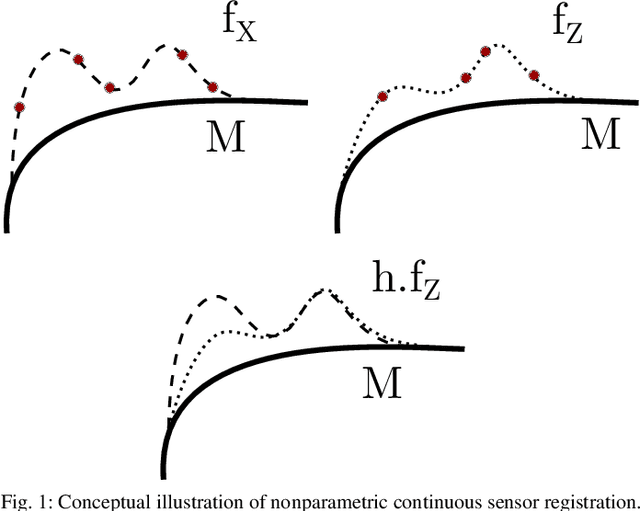
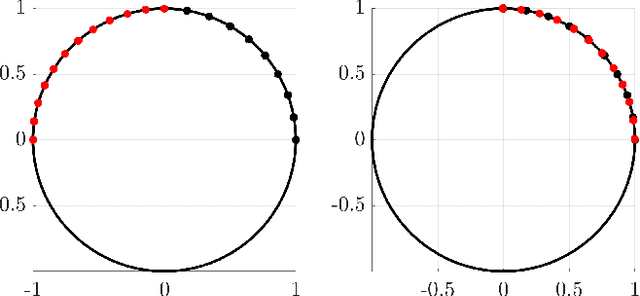
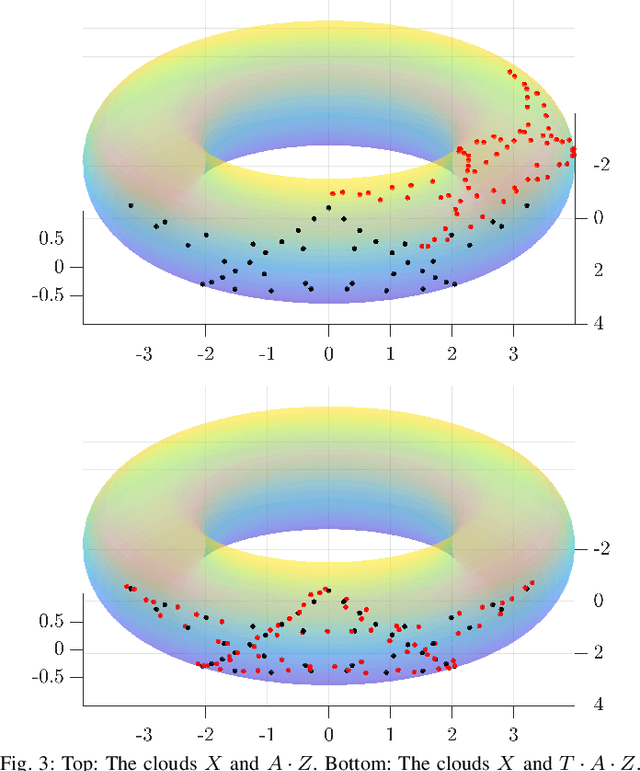
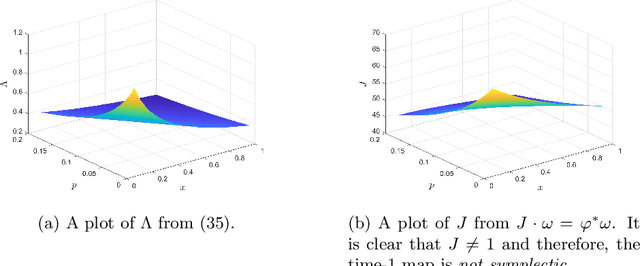
This paper develops a new mathematical framework that enables nonparametric joint semantic/appearance and geometric representation of continuous functions using data. The joint semantic and geometric embedding is modeled by representing the processes in a reproducing kernel Hilbert space. The framework allows the functions to be defined on arbitrary smooth manifolds where the action of a Lie group is used to align them. The continuous functions allow the registration to be independent of a specific signal resolution and the framework is fully analytical with a closed-form derivation of the Riemannian gradient and Hessian. We study a more specialized but widely used case where the Lie group acts on functions isometrically. We solve the problem by maximizing the inner product between two functions defined over data, while the continuous action of the rigid body motion Lie group is captured through the integration of the flow in the corresponding Lie algebra. Low-dimensional cases are derived with numerical examples to show the generality of the proposed framework. The high-dimensional derivation for the special Euclidean group acting on the Euclidean space showcases the point cloud registration and bird's-eye view map registration abilities. A specific derivation and implementation of this framework for RGB-D cameras outperform the state-of-the-art robust visual odometry and performs well in texture and structure-scares environments.

Adaptive Continuous Visual Odometry from RGB-D Images

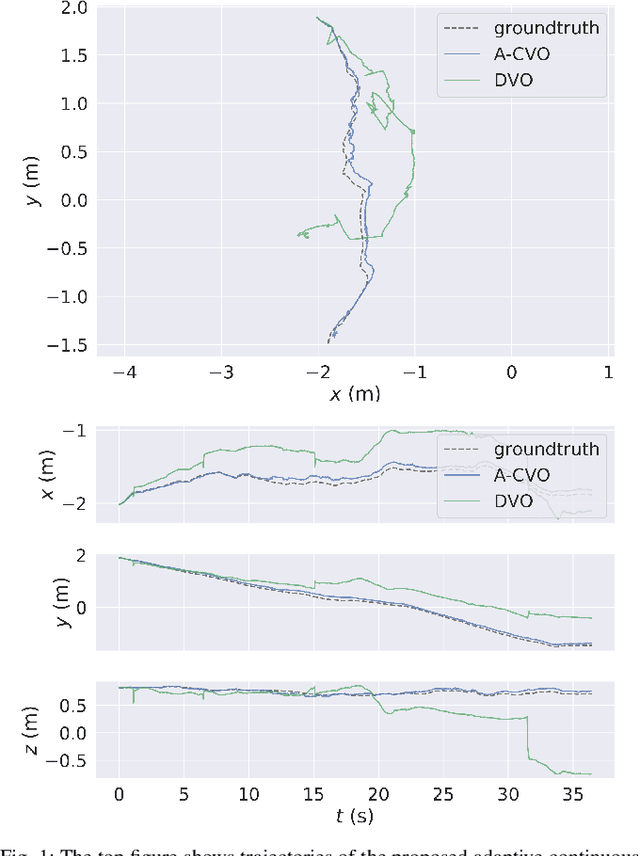
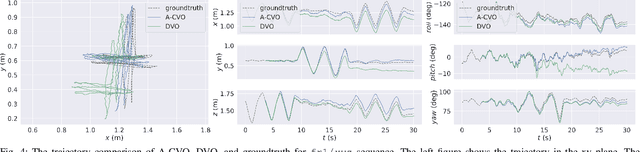
In this paper, we extend the recently developed continuous visual odometry framework for RGB-D cameras to an adaptive framework via online hyperparameter learning. We focus on the case of isotropic kernels with a scalar as the length-scale. In practice and as expected, the length-scale has remarkable impacts on the performance of the original framework. Previously it was handled using a fixed set of conditions within the solver to reduce the length-scale as the algorithm reaches a local minimum. We automate this process by a greedy gradient descent step at each iteration to find the next-best length-scale. Furthermore, to handle failure cases in the gradient descent step where the gradient is not well-behaved, such as the absence of structure or texture in the scene, we use a search interval for the length-scale and guide it gradually toward the smaller values. This latter strategy reverts the adaptive framework to the original setup. The experimental evaluations using publicly available RGB-D benchmarks show the proposed adaptive continuous visual odometry outperforms the original framework and the current state-of-the-art. We also make the software for the developed algorithm publicly available.