The Stabilizer Bootstrap of Quantum Machine Learning with up to 10000 qubits

Quantum machine learning is considered one of the flagship applications of quantum computers, where variational quantum circuits could be the leading paradigm both in the near-term quantum devices and the early fault-tolerant quantum computers. However, it is not clear how to identify the regime of quantum advantages from these circuits, and there is no explicit theory to guide the practical design of variational ansatze to achieve better performance. We address these challenges with the stabilizer bootstrap, a method that uses stabilizer-based techniques to optimize quantum neural networks before their quantum execution, together with theoretical proofs and high-performance computing with 10000 qubits or random datasets up to 1000 data. We find that, in a general setup of variational ansatze, the possibility of improvements from the stabilizer bootstrap depends on the structure of the observables and the size of the datasets. The results reveal that configurations exhibit two distinct behaviors: some maintain a constant probability of circuit improvement, while others show an exponential decay in improvement probability as qubit numbers increase. These patterns are termed strong stabilizer enhancement and weak stabilizer enhancement, respectively, with most situations falling in between. Our work seamlessly bridges techniques from fault-tolerant quantum computing with applications of variational quantum algorithms. Not only does it offer practical insights for designing variational circuits tailored to large-scale machine learning challenges, but it also maps out a clear trajectory for defining the boundaries of feasible and practical quantum advantages.

Deep Learning for Low-Latency, Quantum-Ready RF Sensing

Recent work has shown the promise of applying deep learning to enhance software processing of radio frequency (RF) signals. In parallel, hardware developments with quantum RF sensors based on Rydberg atoms are breaking longstanding barriers in frequency range, resolution, and sensitivity. In this paper, we describe our implementations of quantum-ready machine learning approaches for RF signal classification. Our primary objective is latency: while deep learning offers a more powerful computational paradigm, it also traditionally incurs latency overheads that hinder wider scale deployment. Our work spans three axes. (1) A novel continuous wavelet transform (CWT) based recurrent neural network (RNN) architecture that enables flexible online classification of RF signals on-the-fly with reduced sampling time. (2) Low-latency inference techniques for both GPU and CPU that span over 100x reductions in inference time, enabling real-time operation with sub-millisecond inference. (3) Quantum-readiness validated through application of our models to physics-based simulation of Rydberg atom QRF sensors. Altogether, our work bridges towards next-generation RF sensors that use quantum technology to surpass previous physical limits, paired with latency-optimized AI/ML software that is suitable for real-time deployment.

QuantumSEA: In-Time Sparse Exploration for Noise Adaptive Quantum Circuits

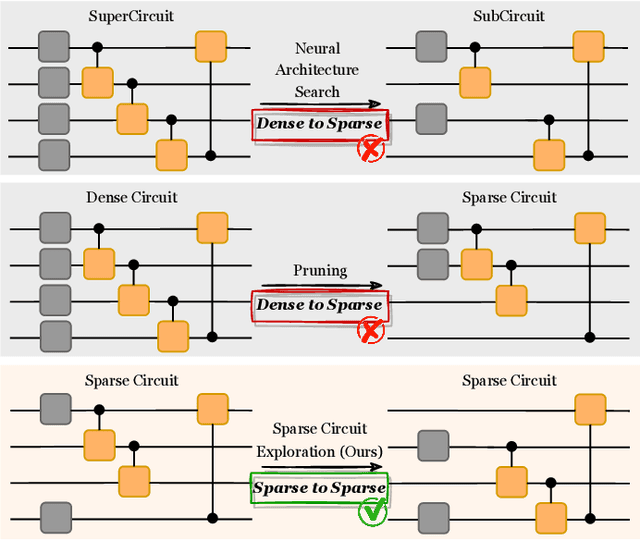
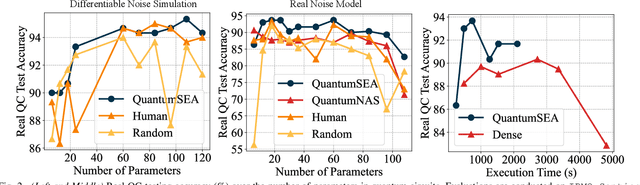
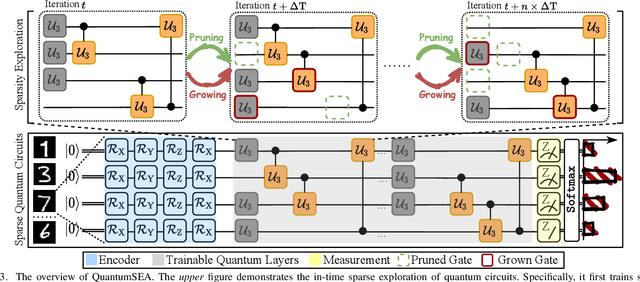
Parameterized Quantum Circuits (PQC) have obtained increasing popularity thanks to their great potential for near-term Noisy Intermediate-Scale Quantum (NISQ) computers. Achieving quantum advantages usually requires a large number of qubits and quantum circuits with enough capacity. However, limited coherence time and massive quantum noises severely constrain the size of quantum circuits that can be executed reliably on real machines. To address these two pain points, we propose QuantumSEA, an in-time sparse exploration for noise-adaptive quantum circuits, aiming to achieve two key objectives: (1) implicit circuits capacity during training - by dynamically exploring the circuit's sparse connectivity and sticking a fixed small number of quantum gates throughout the training which satisfies the coherence time and enjoy light noises, enabling feasible executions on real quantum devices; (2) noise robustness - by jointly optimizing the topology and parameters of quantum circuits under real device noise models. In each update step of sparsity, we leverage the moving average of historical gradients to grow necessary gates and utilize salience-based pruning to eliminate insignificant gates. Extensive experiments are conducted with 7 Quantum Machine Learning (QML) and Variational Quantum Eigensolver (VQE) benchmarks on 6 simulated or real quantum computers, where QuantumSEA consistently surpasses noise-aware search, human-designed, and randomly generated quantum circuit baselines by a clear performance margin. For example, even in the most challenging on-chip training regime, our method establishes state-of-the-art results with only half the number of quantum gates and ~2x time saving of circuit executions. Codes are available at https://github.com/VITA-Group/QuantumSEA.

DGR: Tackling Drifted and Correlated Noise in Quantum Error Correction via Decoding Graph Re-weighting

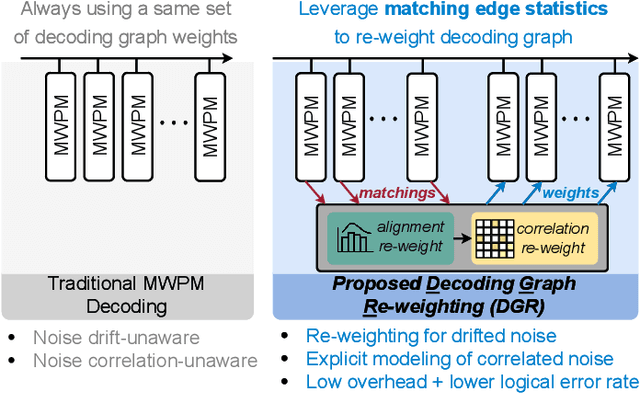
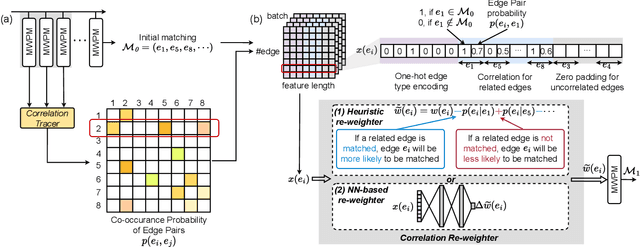
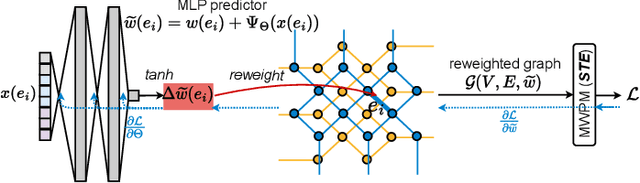
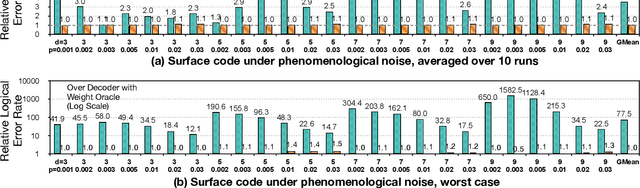
Quantum hardware suffers from high error rates and noise, which makes directly running applications on them ineffective. Quantum Error Correction (QEC) is a critical technique towards fault tolerance which encodes the quantum information distributively in multiple data qubits and uses syndrome qubits to check parity. Minimum-Weight-Perfect-Matching (MWPM) is a popular QEC decoder that takes the syndromes as input and finds the matchings between syndromes that infer the errors. However, there are two paramount challenges for MWPM decoders. First, as noise in real quantum systems can drift over time, there is a potential misalignment with the decoding graph's initial weights, leading to a severe performance degradation in the logical error rates. Second, while the MWPM decoder addresses independent errors, it falls short when encountering correlated errors typical on real hardware, such as those in the 2Q depolarizing channel. We propose DGR, an efficient decoding graph edge re-weighting strategy with no quantum overhead. It leverages the insight that the statistics of matchings across decoding iterations offer rich information about errors on real quantum hardware. By counting the occurrences of edges and edge pairs in decoded matchings, we can statistically estimate the up-to-date probabilities of each edge and the correlations between them. The reweighting process includes two vital steps: alignment re-weighting and correlation re-weighting. The former updates the MWPM weights based on statistics to align with actual noise, and the latter adjusts the weight considering edge correlations. Extensive evaluations on surface code and honeycomb code under various settings show that DGR reduces the logical error rate by 3.6x on average-case noise mismatch with exceeding 5000x improvement under worst-case mismatch.

RobustState: Boosting Fidelity of Quantum State Preparation via Noise-Aware Variational Training

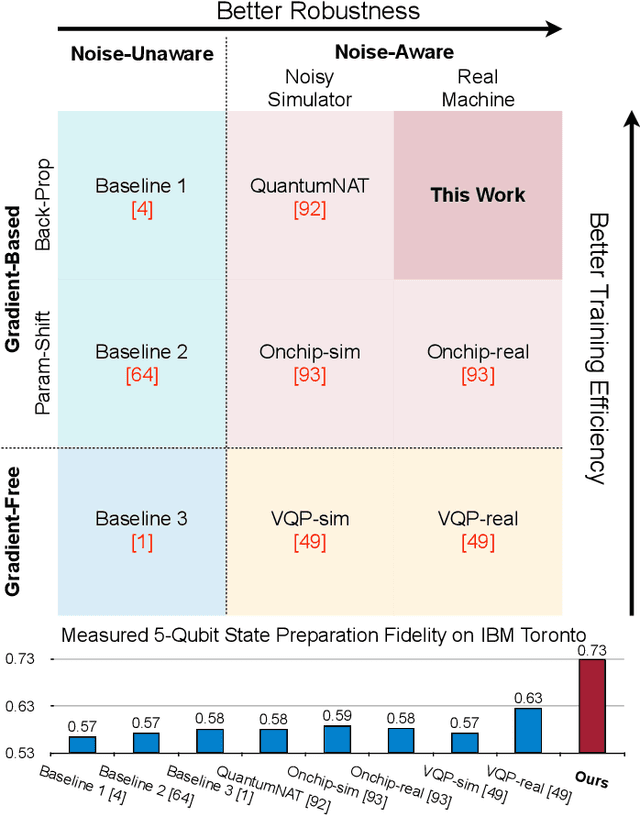
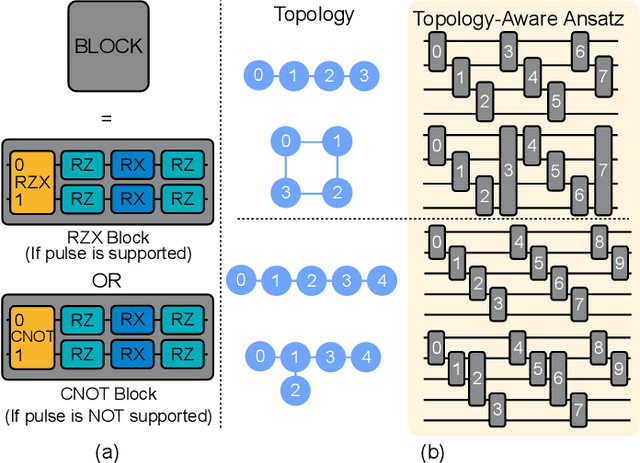
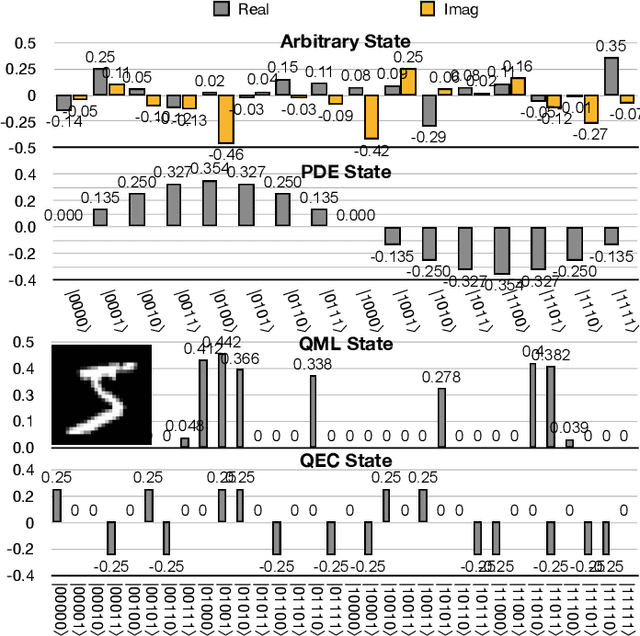
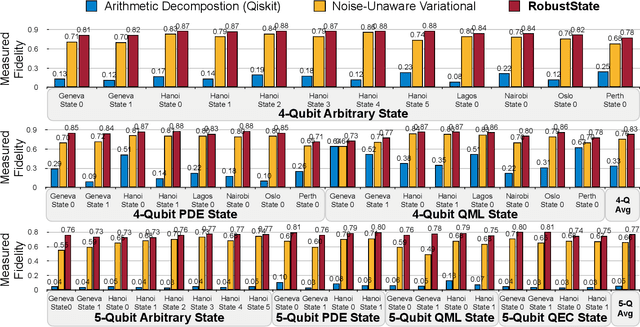
Quantum state preparation, a crucial subroutine in quantum computing, involves generating a target quantum state from initialized qubits. Arbitrary state preparation algorithms can be broadly categorized into arithmetic decomposition (AD) and variational quantum state preparation (VQSP). AD employs a predefined procedure to decompose the target state into a series of gates, whereas VQSP iteratively tunes ansatz parameters to approximate target state. VQSP is particularly apt for Noisy-Intermediate Scale Quantum (NISQ) machines due to its shorter circuits. However, achieving noise-robust parameter optimization still remains challenging. We present RobustState, a novel VQSP training methodology that combines high robustness with high training efficiency. The core idea involves utilizing measurement outcomes from real machines to perform back-propagation through classical simulators, thus incorporating real quantum noise into gradient calculations. RobustState serves as a versatile, plug-and-play technique applicable for training parameters from scratch or fine-tuning existing parameters to enhance fidelity on target machines. It is adaptable to various ansatzes at both gate and pulse levels and can even benefit other variational algorithms, such as variational unitary synthesis. Comprehensive evaluation of RobustState on state preparation tasks for 4 distinct quantum algorithms using 10 real quantum machines demonstrates a coherent error reduction of up to 7.1 $\times$ and state fidelity improvement of up to 96\% and 81\% for 4-Q and 5-Q states, respectively. On average, RobustState improves fidelity by 50\% and 72\% for 4-Q and 5-Q states compared to baseline approaches.

Training Quantum Boltzmann Machines with Coresets

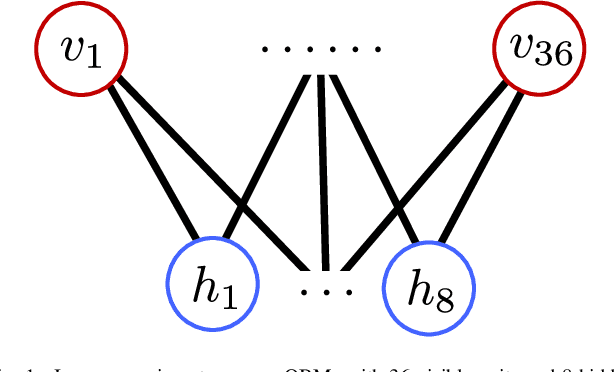
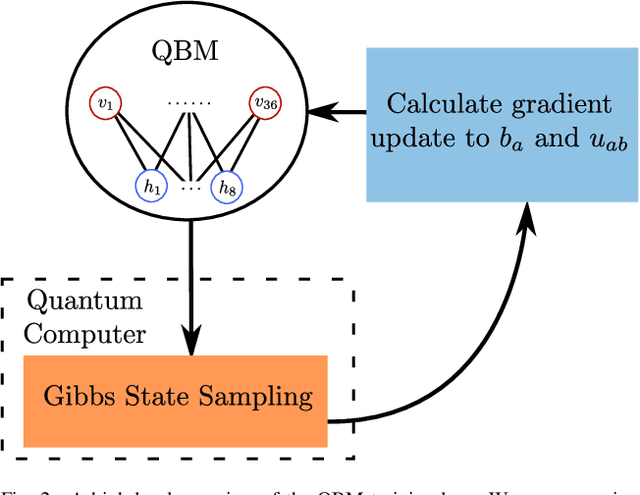
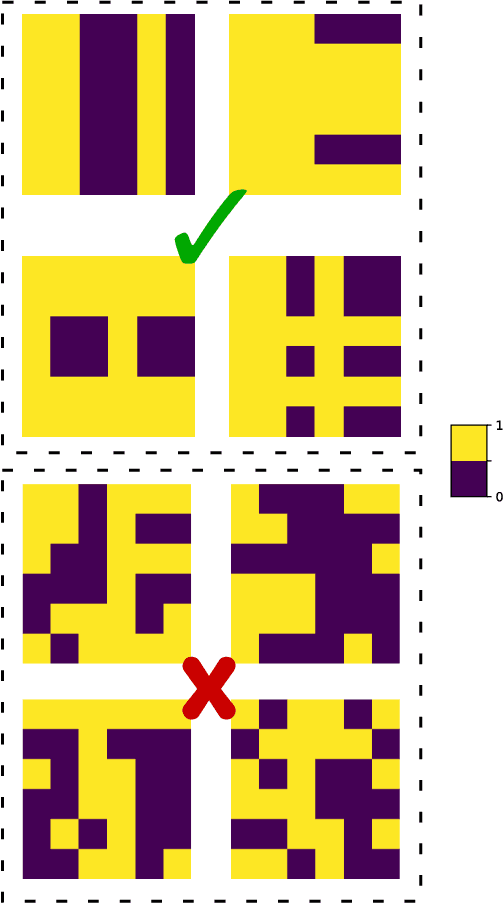
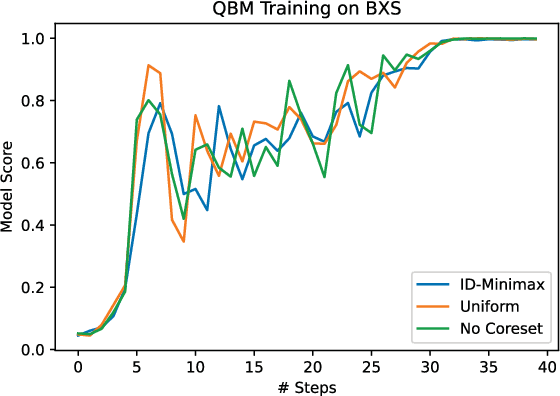
Recent work has proposed and explored using coreset techniques for quantum algorithms that operate on classical data sets to accelerate the applicability of these algorithms on near-term quantum devices. We apply these ideas to Quantum Boltzmann Machines (QBM) where gradient-based steps which require Gibbs state sampling are the main computational bottleneck during training. By using a coreset in place of the full data set, we try to minimize the number of steps needed and accelerate the overall training time. In a regime where computational time on quantum computers is a precious resource, we propose this might lead to substantial practical savings. We evaluate this approach on 6x6 binary images from an augmented bars and stripes data set using a QBM with 36 visible units and 8 hidden units. Using an Inception score inspired metric, we compare QBM training times with and without using coresets.

Fundamental causal bounds of quantum random access memories

Quantum devices should operate in adherence to quantum physics principles. Quantum random access memory (QRAM), a fundamental component of many essential quantum algorithms for tasks such as linear algebra, data search, and machine learning, is often proposed to offer $\mathcal{O}(\log N)$ circuit depth for $\mathcal{O}(N)$ data size, given $N$ qubits. However, this claim appears to breach the principle of relativity when dealing with a large number of qubits in quantum materials interacting locally. In our study we critically explore the intrinsic bounds of rapid quantum memories based on causality, employing the relativistic quantum field theory and Lieb-Robinson bounds in quantum many-body systems. In this paper, we consider a hardware-efficient QRAM design in hybrid quantum acoustic systems. Assuming clock cycle times of approximately $10^{-3}$ seconds and a lattice spacing of about 1 micrometer, we show that QRAM can accommodate up to $\mathcal{O}(10^7)$ logical qubits in 1 dimension, $\mathcal{O}(10^{15})$ to $\mathcal{O}(10^{20})$ in various 2D architectures, and $\mathcal{O}(10^{24})$ in 3 dimensions. We contend that this causality bound broadly applies to other quantum hardware systems. Our findings highlight the impact of fundamental quantum physics constraints on the long-term performance of quantum computing applications in data science and suggest potential quantum memory designs for performance enhancement.

Spacetime-Efficient Low-Depth Quantum State Preparation with Applications

We propose a novel deterministic method for preparing arbitrary quantum states, and we show that it requires asymptotically fewer quantum resources than previous methods. When our protocol is compiled into CNOT and arbitrary single-qubit gates, it prepares an $N$-dimensional state in depth $O(\log(N))$ and spacetime allocation (a metric that accounts for the fact that oftentimes some ancilla qubits need not be active for the entire protocol) $O(N)$, which are both optimal and not simultaneously achieved by previous methods. When compiled into the $\{\mathrm{H,S,T,CNOT}\}$ gate set, it prepares an arbitrary state up to error $\epsilon$ in depth $O(\log(N/\epsilon))$ and spacetime allocation $O(N\log(\log(N)/\epsilon))$, improving over $O(\log(N)\log(N/\epsilon))$ and $O(N\log(N/\epsilon))$, respectively. We illustrate how the reduced spacetime allocation of our protocol enables rapid preparation of many disjoint states with only constant-factor ancilla overhead -- $O(N)$ ancilla qubits are reused efficiently to prepare a product state of $w$ $N$-dimensional states in depth $O(w + \log(N))$ rather than $O(w\log(N))$, achieving effectively constant depth per state. We highlight several applications where this ability would be useful, including quantum machine learning, Hamiltonian simulation, and solving linear systems of equations. We provide quantum circuit descriptions of our protocol along with detailed pseudocode.

Benchmarking variational quantum circuits with permutation symmetry

We propose SnCQA, a set of hardware-efficient variational circuits of equivariant quantum convolutional circuits respective to permutation symmetries and spatial lattice symmetries with the number of qubits $n$. By exploiting permutation symmetries of the system, such as lattice Hamiltonians common to many quantum many-body and quantum chemistry problems, Our quantum neural networks are suitable for solving machine learning problems where permutation symmetries are present, which could lead to significant savings of computational costs. Aside from its theoretical novelty, we find our simulations perform well in practical instances of learning ground states in quantum computational chemistry, where we could achieve comparable performances to traditional methods with few tens of parameters. Compared to other traditional variational quantum circuits, such as the pure hardware-efficient ansatz (pHEA), we show that SnCQA is more scalable, accurate, and noise resilient (with $20\times$ better performance on $3 \times 4$ square lattice and $200\% - 1000\%$ resource savings in various lattice sizes and key criterions such as the number of layers, parameters, and times to converge in our cases), suggesting a potentially favorable experiment on near-time quantum devices.

QuEst: Graph Transformer for Quantum Circuit Reliability Estimation

Among different quantum algorithms, PQC for QML show promises on near-term devices. To facilitate the QML and PQC research, a recent python library called TorchQuantum has been released. It can construct, simulate, and train PQC for machine learning tasks with high speed and convenient debugging supports. Besides quantum for ML, we want to raise the community's attention on the reversed direction: ML for quantum. Specifically, the TorchQuantum library also supports using data-driven ML models to solve problems in quantum system research, such as predicting the impact of quantum noise on circuit fidelity and improving the quantum circuit compilation efficiency. This paper presents a case study of the ML for quantum part. Since estimating the noise impact on circuit reliability is an essential step toward understanding and mitigating noise, we propose to leverage classical ML to predict noise impact on circuit fidelity. Inspired by the natural graph representation of quantum circuits, we propose to leverage a graph transformer model to predict the noisy circuit fidelity. We firstly collect a large dataset with a variety of quantum circuits and obtain their fidelity on noisy simulators and real machines. Then we embed each circuit into a graph with gate and noise properties as node features, and adopt a graph transformer to predict the fidelity. Evaluated on 5 thousand random and algorithm circuits, the graph transformer predictor can provide accurate fidelity estimation with RMSE error 0.04 and outperform a simple neural network-based model by 0.02 on average. It can achieve 0.99 and 0.95 R$^2$ scores for random and algorithm circuits, respectively. Compared with circuit simulators, the predictor has over 200X speedup for estimating the fidelity.