Refining Positive and Toxic Samples for Dual Safety Self-Alignment of LLMs with Minimal Human Interventions

Recent AI agents, such as ChatGPT and LLaMA, primarily rely on instruction tuning and reinforcement learning to calibrate the output of large language models (LLMs) with human intentions, ensuring the outputs are harmless and helpful. Existing methods heavily depend on the manual annotation of high-quality positive samples, while contending with issues such as noisy labels and minimal distinctions between preferred and dispreferred response data. However, readily available toxic samples with clear safety distinctions are often filtered out, removing valuable negative references that could aid LLMs in safety alignment. In response, we propose PT-ALIGN, a novel safety self-alignment approach that minimizes human supervision by automatically refining positive and toxic samples and performing fine-grained dual instruction tuning. Positive samples are harmless responses, while toxic samples deliberately contain extremely harmful content, serving as a new supervisory signals. Specifically, we utilize LLM itself to iteratively generate and refine training instances by only exploring fewer than 50 human annotations. We then employ two losses, i.e., maximum likelihood estimation (MLE) and fine-grained unlikelihood training (UT), to jointly learn to enhance the LLM's safety. The MLE loss encourages an LLM to maximize the generation of harmless content based on positive samples. Conversely, the fine-grained UT loss guides the LLM to minimize the output of harmful words based on negative samples at the token-level, thereby guiding the model to decouple safety from effectiveness, directing it toward safer fine-tuning objectives, and increasing the likelihood of generating helpful and reliable content. Experiments on 9 popular open-source LLMs demonstrate the effectiveness of our PT-ALIGN for safety alignment, while maintaining comparable levels of helpfulness and usefulness.

DGR: Tackling Drifted and Correlated Noise in Quantum Error Correction via Decoding Graph Re-weighting

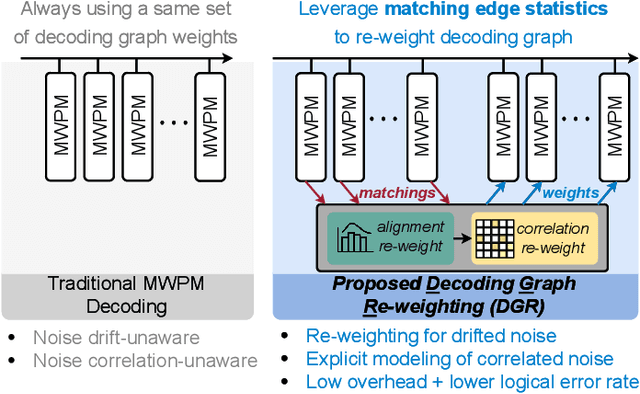
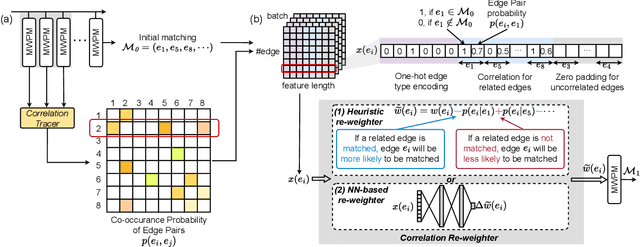
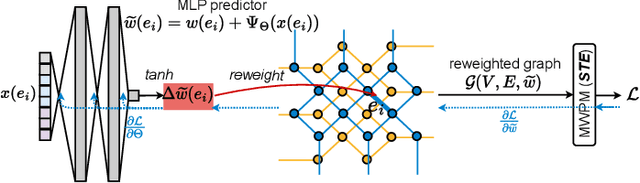
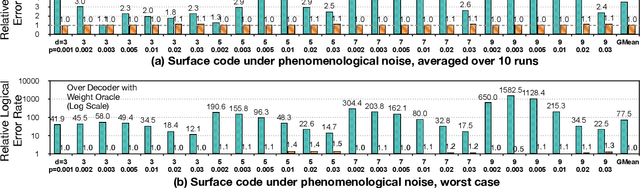
Quantum hardware suffers from high error rates and noise, which makes directly running applications on them ineffective. Quantum Error Correction (QEC) is a critical technique towards fault tolerance which encodes the quantum information distributively in multiple data qubits and uses syndrome qubits to check parity. Minimum-Weight-Perfect-Matching (MWPM) is a popular QEC decoder that takes the syndromes as input and finds the matchings between syndromes that infer the errors. However, there are two paramount challenges for MWPM decoders. First, as noise in real quantum systems can drift over time, there is a potential misalignment with the decoding graph's initial weights, leading to a severe performance degradation in the logical error rates. Second, while the MWPM decoder addresses independent errors, it falls short when encountering correlated errors typical on real hardware, such as those in the 2Q depolarizing channel. We propose DGR, an efficient decoding graph edge re-weighting strategy with no quantum overhead. It leverages the insight that the statistics of matchings across decoding iterations offer rich information about errors on real quantum hardware. By counting the occurrences of edges and edge pairs in decoded matchings, we can statistically estimate the up-to-date probabilities of each edge and the correlations between them. The reweighting process includes two vital steps: alignment re-weighting and correlation re-weighting. The former updates the MWPM weights based on statistics to align with actual noise, and the latter adjusts the weight considering edge correlations. Extensive evaluations on surface code and honeycomb code under various settings show that DGR reduces the logical error rate by 3.6x on average-case noise mismatch with exceeding 5000x improvement under worst-case mismatch.

RobustState: Boosting Fidelity of Quantum State Preparation via Noise-Aware Variational Training

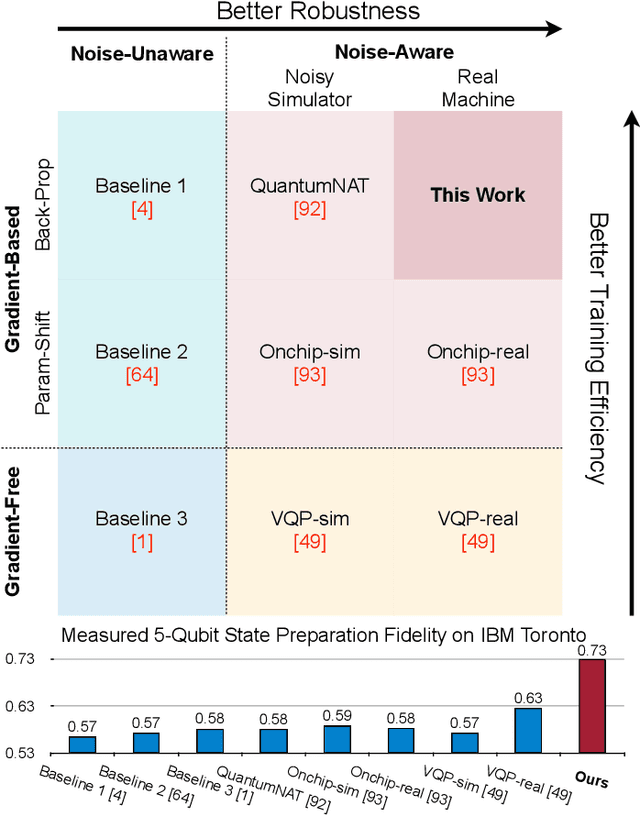
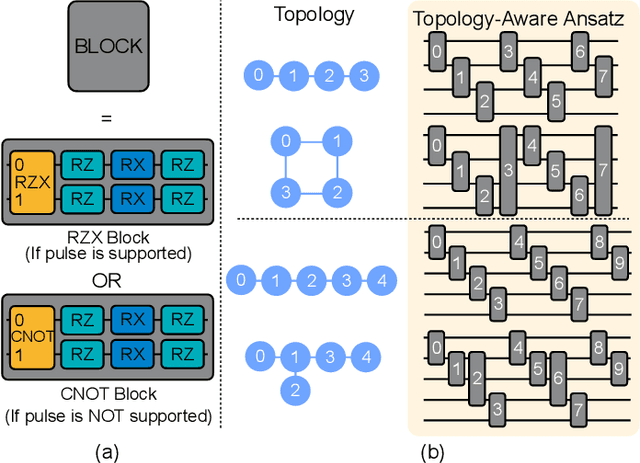
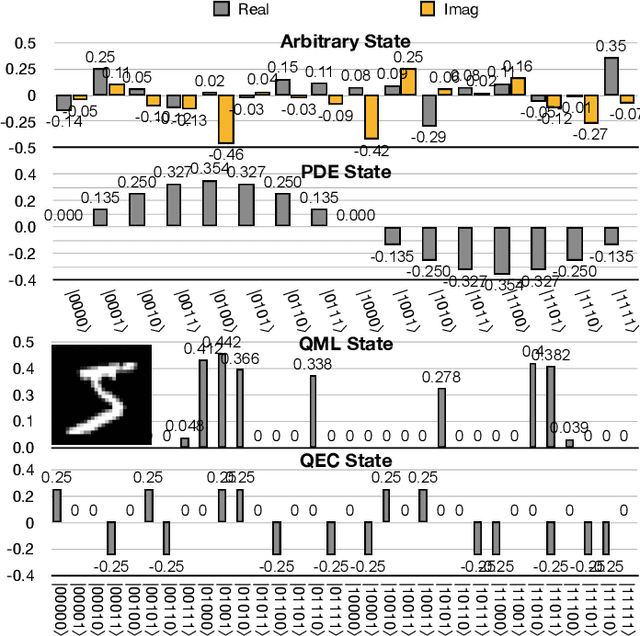
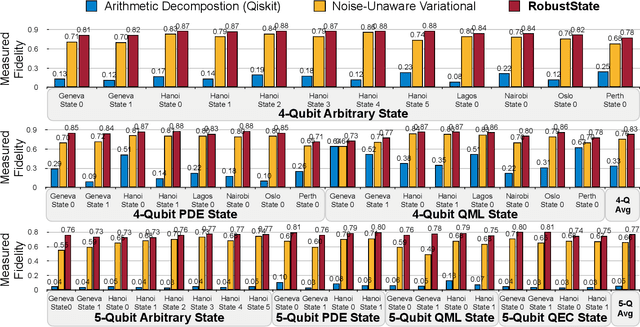
Quantum state preparation, a crucial subroutine in quantum computing, involves generating a target quantum state from initialized qubits. Arbitrary state preparation algorithms can be broadly categorized into arithmetic decomposition (AD) and variational quantum state preparation (VQSP). AD employs a predefined procedure to decompose the target state into a series of gates, whereas VQSP iteratively tunes ansatz parameters to approximate target state. VQSP is particularly apt for Noisy-Intermediate Scale Quantum (NISQ) machines due to its shorter circuits. However, achieving noise-robust parameter optimization still remains challenging. We present RobustState, a novel VQSP training methodology that combines high robustness with high training efficiency. The core idea involves utilizing measurement outcomes from real machines to perform back-propagation through classical simulators, thus incorporating real quantum noise into gradient calculations. RobustState serves as a versatile, plug-and-play technique applicable for training parameters from scratch or fine-tuning existing parameters to enhance fidelity on target machines. It is adaptable to various ansatzes at both gate and pulse levels and can even benefit other variational algorithms, such as variational unitary synthesis. Comprehensive evaluation of RobustState on state preparation tasks for 4 distinct quantum algorithms using 10 real quantum machines demonstrates a coherent error reduction of up to 7.1 $\times$ and state fidelity improvement of up to 96\% and 81\% for 4-Q and 5-Q states, respectively. On average, RobustState improves fidelity by 50\% and 72\% for 4-Q and 5-Q states compared to baseline approaches.