The Stabilizer Bootstrap of Quantum Machine Learning with up to 10000 qubits

Quantum machine learning is considered one of the flagship applications of quantum computers, where variational quantum circuits could be the leading paradigm both in the near-term quantum devices and the early fault-tolerant quantum computers. However, it is not clear how to identify the regime of quantum advantages from these circuits, and there is no explicit theory to guide the practical design of variational ansatze to achieve better performance. We address these challenges with the stabilizer bootstrap, a method that uses stabilizer-based techniques to optimize quantum neural networks before their quantum execution, together with theoretical proofs and high-performance computing with 10000 qubits or random datasets up to 1000 data. We find that, in a general setup of variational ansatze, the possibility of improvements from the stabilizer bootstrap depends on the structure of the observables and the size of the datasets. The results reveal that configurations exhibit two distinct behaviors: some maintain a constant probability of circuit improvement, while others show an exponential decay in improvement probability as qubit numbers increase. These patterns are termed strong stabilizer enhancement and weak stabilizer enhancement, respectively, with most situations falling in between. Our work seamlessly bridges techniques from fault-tolerant quantum computing with applications of variational quantum algorithms. Not only does it offer practical insights for designing variational circuits tailored to large-scale machine learning challenges, but it also maps out a clear trajectory for defining the boundaries of feasible and practical quantum advantages.

Quantum Hamiltonian Descent for Graph Partition

We introduce Quantum Hamiltonian Descent as a novel approach to solve the graph partition problem. By reformulating graph partition as a Quadratic Unconstrained Binary Optimization (QUBO) problem, we leverage QHD's quantum-inspired dynamics to identify optimal community structures. Our method implements a multi-level refinement strategy that alternates between QUBO formulation and QHD optimization to iteratively improve partition quality. Experimental results demonstrate that our QHD-based approach achieves superior modularity scores (up to 5.49\%) improvement with reduced computational overhead compared to traditional optimization methods. This work establishes QHD as an effective quantum-inspired framework for tackling graph partition challenges in large-scale networks.

Quantum-machine-assisted Drug Discovery: Survey and Perspective

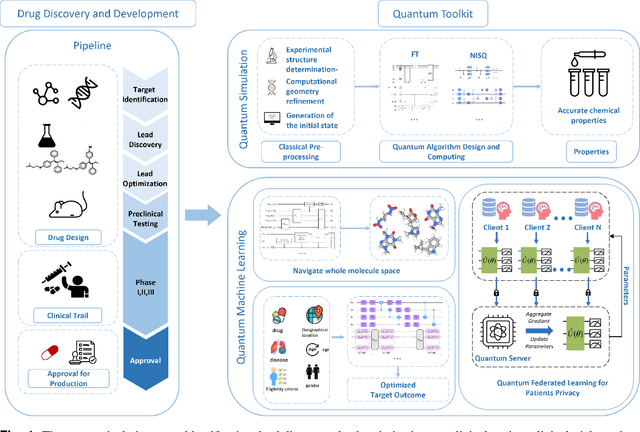
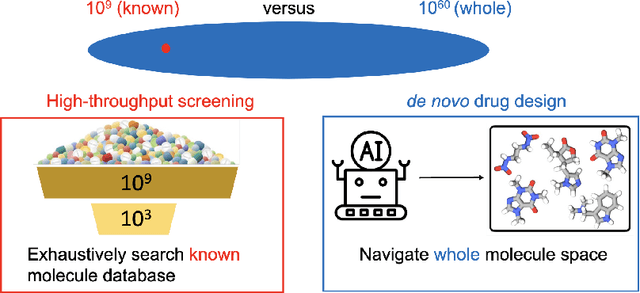
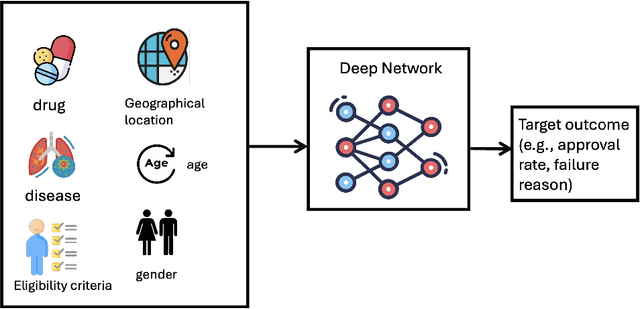
Drug discovery and development is a highly complex and costly endeavor, typically requiring over a decade and substantial financial investment to bring a new drug to market. Traditional computer-aided drug design (CADD) has made significant progress in accelerating this process, but the development of quantum computing offers potential due to its unique capabilities. This paper discusses the integration of quantum computing into drug discovery and development, focusing on how quantum technologies might accelerate and enhance various stages of the drug development cycle. Specifically, we explore the application of quantum computing in addressing challenges related to drug discovery, such as molecular simulation and the prediction of drug-target interactions, as well as the optimization of clinical trial outcomes. By leveraging the inherent capabilities of quantum computing, we might be able to reduce the time and cost associated with bringing new drugs to market, ultimately benefiting public health.

Graph Learning for Parameter Prediction of Quantum Approximate Optimization Algorithm

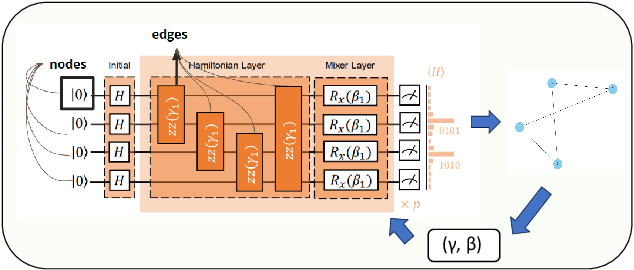
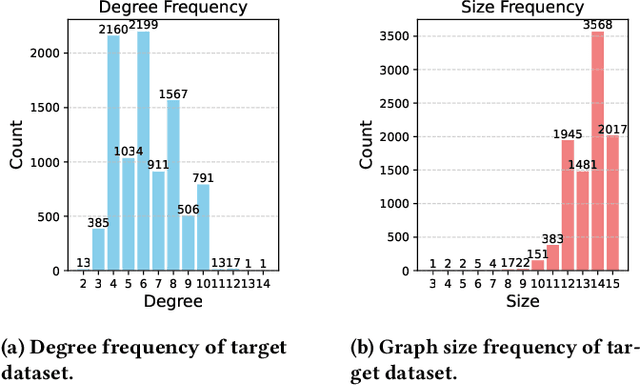
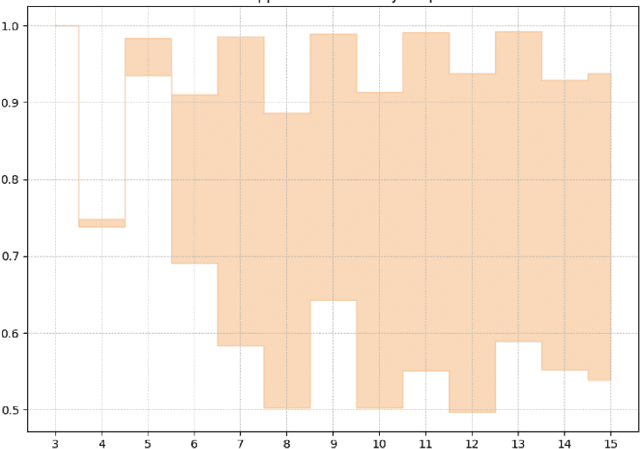
In recent years, quantum computing has emerged as a transformative force in the field of combinatorial optimization, offering novel approaches to tackling complex problems that have long challenged classical computational methods. Among these, the Quantum Approximate Optimization Algorithm (QAOA) stands out for its potential to efficiently solve the Max-Cut problem, a quintessential example of combinatorial optimization. However, practical application faces challenges due to current limitations on quantum computational resource. Our work optimizes QAOA initialization, using Graph Neural Networks (GNN) as a warm-start technique. This sacrifices affordable computational resource on classical computer to reduce quantum computational resource overhead, enhancing QAOA's effectiveness. Experiments with various GNN architectures demonstrate the adaptability and stability of our framework, highlighting the synergy between quantum algorithms and machine learning. Our findings show GNN's potential in improving QAOA performance, opening new avenues for hybrid quantum-classical approaches in quantum computing and contributing to practical applications.

RobustState: Boosting Fidelity of Quantum State Preparation via Noise-Aware Variational Training

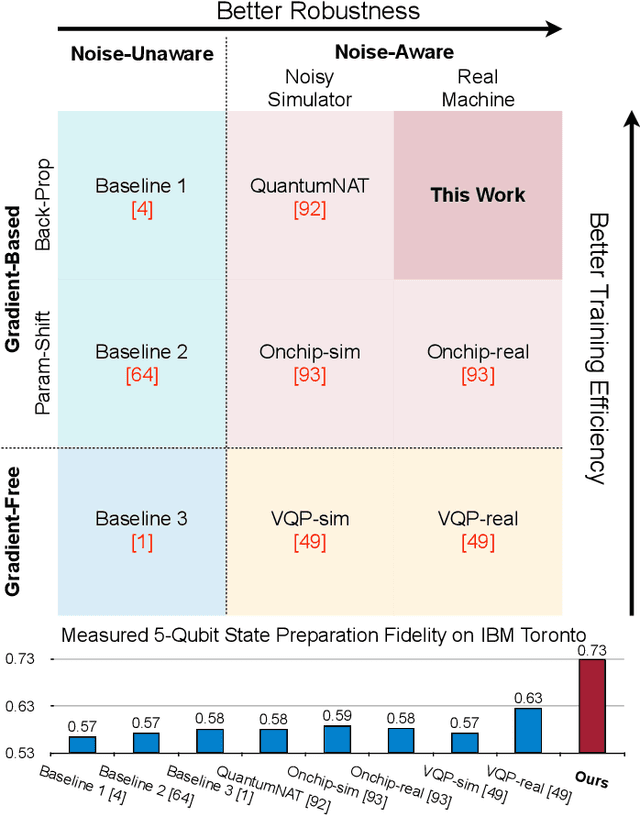
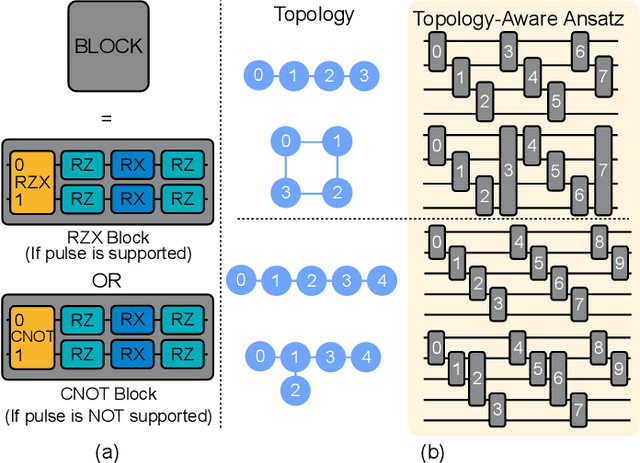
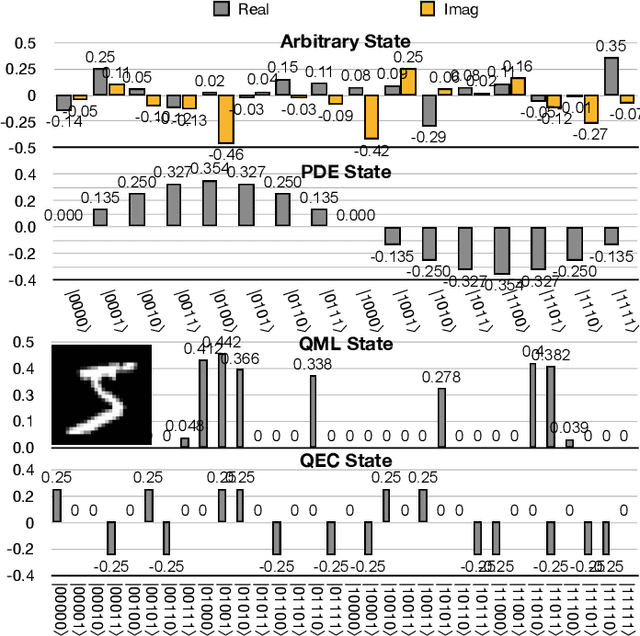
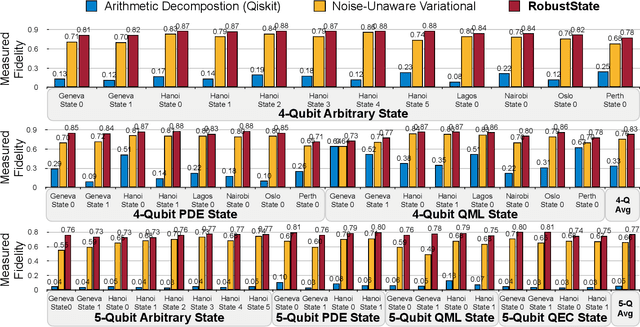
Quantum state preparation, a crucial subroutine in quantum computing, involves generating a target quantum state from initialized qubits. Arbitrary state preparation algorithms can be broadly categorized into arithmetic decomposition (AD) and variational quantum state preparation (VQSP). AD employs a predefined procedure to decompose the target state into a series of gates, whereas VQSP iteratively tunes ansatz parameters to approximate target state. VQSP is particularly apt for Noisy-Intermediate Scale Quantum (NISQ) machines due to its shorter circuits. However, achieving noise-robust parameter optimization still remains challenging. We present RobustState, a novel VQSP training methodology that combines high robustness with high training efficiency. The core idea involves utilizing measurement outcomes from real machines to perform back-propagation through classical simulators, thus incorporating real quantum noise into gradient calculations. RobustState serves as a versatile, plug-and-play technique applicable for training parameters from scratch or fine-tuning existing parameters to enhance fidelity on target machines. It is adaptable to various ansatzes at both gate and pulse levels and can even benefit other variational algorithms, such as variational unitary synthesis. Comprehensive evaluation of RobustState on state preparation tasks for 4 distinct quantum algorithms using 10 real quantum machines demonstrates a coherent error reduction of up to 7.1 $\times$ and state fidelity improvement of up to 96\% and 81\% for 4-Q and 5-Q states, respectively. On average, RobustState improves fidelity by 50\% and 72\% for 4-Q and 5-Q states compared to baseline approaches.

QuEst: Graph Transformer for Quantum Circuit Reliability Estimation

Among different quantum algorithms, PQC for QML show promises on near-term devices. To facilitate the QML and PQC research, a recent python library called TorchQuantum has been released. It can construct, simulate, and train PQC for machine learning tasks with high speed and convenient debugging supports. Besides quantum for ML, we want to raise the community's attention on the reversed direction: ML for quantum. Specifically, the TorchQuantum library also supports using data-driven ML models to solve problems in quantum system research, such as predicting the impact of quantum noise on circuit fidelity and improving the quantum circuit compilation efficiency. This paper presents a case study of the ML for quantum part. Since estimating the noise impact on circuit reliability is an essential step toward understanding and mitigating noise, we propose to leverage classical ML to predict noise impact on circuit fidelity. Inspired by the natural graph representation of quantum circuits, we propose to leverage a graph transformer model to predict the noisy circuit fidelity. We firstly collect a large dataset with a variety of quantum circuits and obtain their fidelity on noisy simulators and real machines. Then we embed each circuit into a graph with gate and noise properties as node features, and adopt a graph transformer to predict the fidelity. Evaluated on 5 thousand random and algorithm circuits, the graph transformer predictor can provide accurate fidelity estimation with RMSE error 0.04 and outperform a simple neural network-based model by 0.02 on average. It can achieve 0.99 and 0.95 R$^2$ scores for random and algorithm circuits, respectively. Compared with circuit simulators, the predictor has over 200X speedup for estimating the fidelity.

PAN: Pulse Ansatz on NISQ Machines

Variational quantum algorithms (VQAs) have demonstrated great potentials in the NISQ era. In the workflow of VQA, the parameters of ansatz are iteratively updated to approximate the desired quantum states. We have seen various efforts to draft better ansatz with less gates. In quantum computers, the gate ansatz will eventually be transformed into control signals such as microwave pulses on transmons. And the control pulses need elaborate calibration to minimize the errors such as over-rotation and under-rotation. In the case of VQAs, this procedure will introduce redundancy, but the variational properties of VQAs can naturally handle problems of over-rotation and under-rotation by updating the amplitude and frequency parameters. Therefore, we propose PAN, a native-pulse ansatz generator framework for VQAs. We generate native-pulse ansatz with trainable parameters for amplitudes and frequencies. In our proposed PAN, we are tuning parametric pulses, which are natively supported on NISQ computers. Considering that parameter-shift rules do not hold for native-pulse ansatz, we need to deploy non-gradient optimizers. To constrain the number of parameters sent to the optimizer, we adopt a progressive way to generate our native-pulse ansatz. Experiments are conducted on both simulators and quantum devices to validate our methods. When adopted on NISQ machines, PAN obtained improved the performance with decreased latency by an average of 86%. PAN is able to achieve 99.336% and 96.482% accuracy for VQE tasks on H2 and HeH+ respectively, even with considerable noises in NISQ machines.