Zhixin Song
Graph Learning for Parameter Prediction of Quantum Approximate Optimization Algorithm
Mar 05, 2024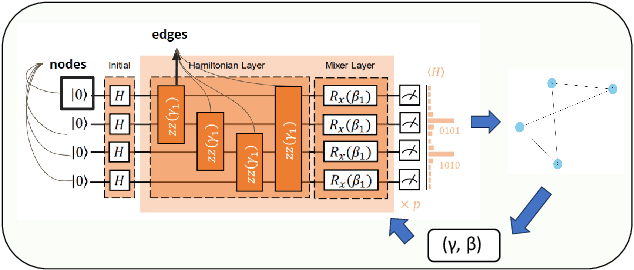

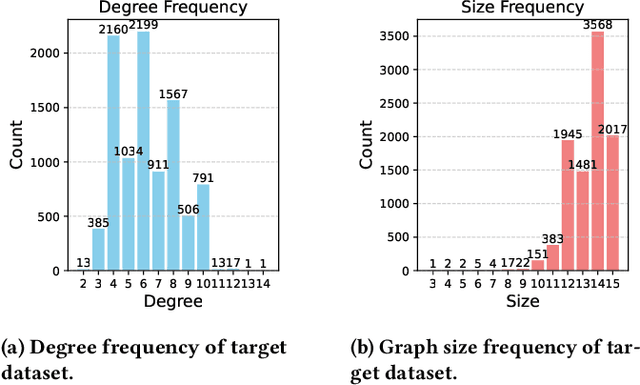
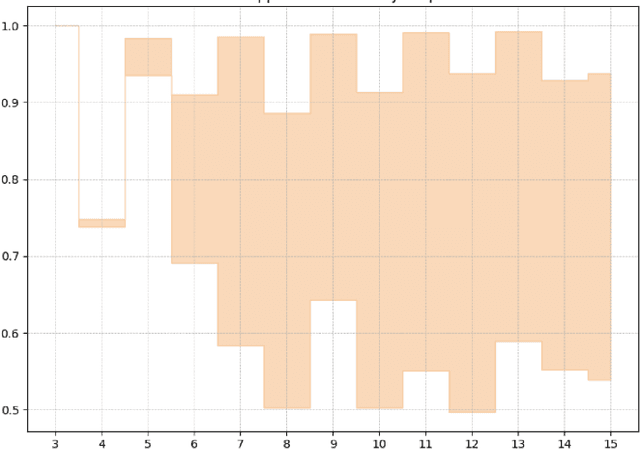
Abstract:In recent years, quantum computing has emerged as a transformative force in the field of combinatorial optimization, offering novel approaches to tackling complex problems that have long challenged classical computational methods. Among these, the Quantum Approximate Optimization Algorithm (QAOA) stands out for its potential to efficiently solve the Max-Cut problem, a quintessential example of combinatorial optimization. However, practical application faces challenges due to current limitations on quantum computational resource. Our work optimizes QAOA initialization, using Graph Neural Networks (GNN) as a warm-start technique. This sacrifices affordable computational resource on classical computer to reduce quantum computational resource overhead, enhancing QAOA's effectiveness. Experiments with various GNN architectures demonstrate the adaptability and stability of our framework, highlighting the synergy between quantum algorithms and machine learning. Our findings show GNN's potential in improving QAOA performance, opening new avenues for hybrid quantum-classical approaches in quantum computing and contributing to practical applications.
Privacy-preserving quantum federated learning via gradient hiding
Dec 07, 2023Abstract:Distributed quantum computing, particularly distributed quantum machine learning, has gained substantial prominence for its capacity to harness the collective power of distributed quantum resources, transcending the limitations of individual quantum nodes. Meanwhile, the critical concern of privacy within distributed computing protocols remains a significant challenge, particularly in standard classical federated learning (FL) scenarios where data of participating clients is susceptible to leakage via gradient inversion attacks by the server. This paper presents innovative quantum protocols with quantum communication designed to address the FL problem, strengthen privacy measures, and optimize communication efficiency. In contrast to previous works that leverage expressive variational quantum circuits or differential privacy techniques, we consider gradient information concealment using quantum states and propose two distinct FL protocols, one based on private inner-product estimation and the other on incremental learning. These protocols offer substantial advancements in privacy preservation with low communication resources, forging a path toward efficient quantum communication-assisted FL protocols and contributing to the development of secure distributed quantum machine learning, thus addressing critical privacy concerns in the quantum computing era.
LOCCNet: a machine learning framework for distributed quantum information processing
Jan 28, 2021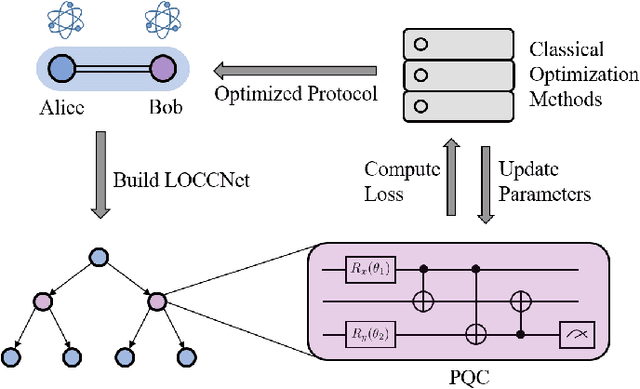
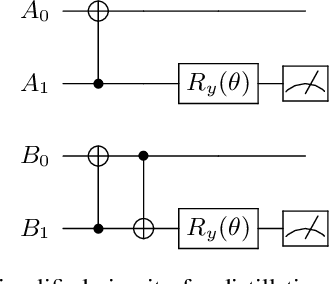
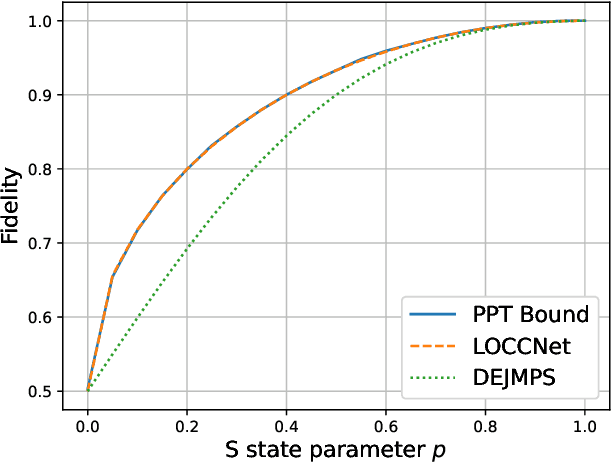
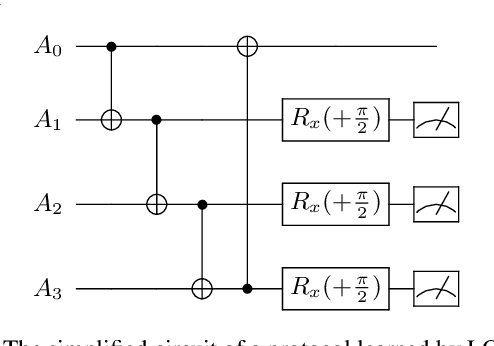
Abstract:Distributed quantum information processing is essential for building quantum networks and enabling more extensive quantum computations. In this regime, several spatially separated parties share a multipartite quantum system, and the most natural set of operations are Local Operations and Classical Communication (LOCC). As a pivotal part in quantum information theory and practice, LOCC has led to many vital protocols such as quantum teleportation. However, designing practical LOCC protocols is challenging due to LOCC's intractable structure and limitations set by near-term quantum devices. Here we introduce LOCCNet, a machine learning framework facilitating protocol design and optimization for distributed quantum information processing tasks. As applications, we explore various quantum information tasks such as entanglement distillation, quantum state discrimination, and quantum channel simulation. We discover novel protocols with evident improvements, in particular, for entanglement distillation with quantum states of interest in quantum information. Our approach opens up new opportunities for exploring entanglement and its applications with machine learning, which will potentially sharpen our understanding of the power and limitations of LOCC.
VSQL: Variational Shadow Quantum Learning for Classification
Dec 15, 2020



Abstract:Classification of quantum data is essential for quantum machine learning and near-term quantum technologies. In this paper, we propose a new hybrid quantum-classical framework for supervised quantum learning, which we call Variational Shadow Quantum Learning (VSQL). Our method in particular utilizes the classical shadows of quantum data, which fundamentally represent the side information of quantum data with respect to certain physical observables. Specifically, we first use variational shadow quantum circuits to extract classical features in a convolution way and then utilize a fully-connected neural network to complete the classification task. We show that this method could sharply reduce the number of parameters and thus better facilitate quantum circuit training. Simultaneously, less noise will be introduced since fewer quantum gates are employed in such shadow circuits. Moreover, we show that the Barren Plateau issue, a significant gradient vanishing problem in quantum machine learning, could be avoided in VSQL. Finally, we demonstrate the efficiency of VSQL in quantum classification via numerical experiments on the classification of quantum states and the recognition of multi-labeled handwritten digits. In particular, our VSQL approach outperforms existing variational quantum classifiers in the test accuracy in the binary case of handwritten digit recognition and notably requires much fewer parameters.
Variational Quantum Singular Value Decomposition
Jun 03, 2020



Abstract:Singular value decomposition is central to many problems in both engineering and scientific fields. Several quantum algorithms have been proposed to determine the singular values and their associated singular vectors of a given matrix. Although these quantum algorithms are promising, the required quantum subroutines and resources are too costly on near-term quantum devices. In this work, we propose a variational quantum algorithm for singular value decomposition (VQSVD). By exploiting the variational principles for singular values and the Ky Fan Theorem, we design a novel loss function such that two quantum neural networks or parameterized quantum circuits could be trained to learn the singular vectors and output the corresponding singular values. We further conduct numerical simulations of the algorithm for singular-value decomposition of random matrices as well as its applications in image compression of handwritten digits. Finally, we discuss the applications of our algorithm in systems of linear equations, least squares estimation, and recommendation systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge