A Hybrid Quantum-Classical Hamiltonian Learning Algorithm

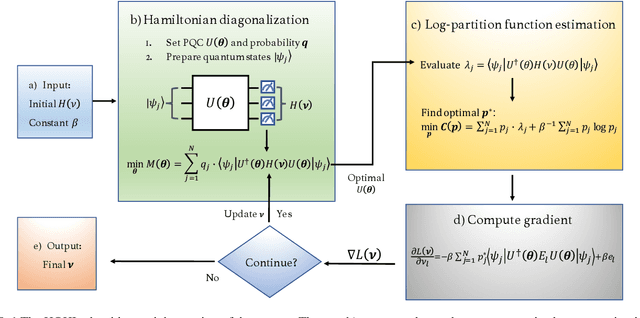
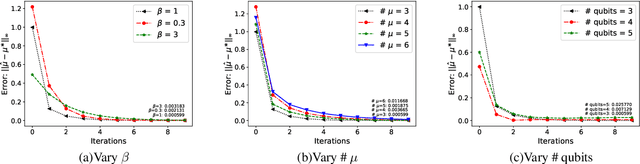
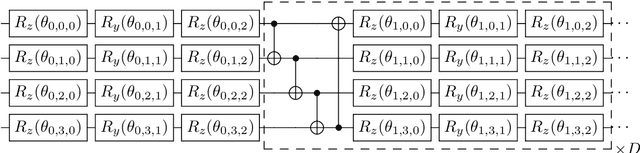
Hamiltonian learning is crucial to the certification of quantum devices and quantum simulators. In this paper, we propose a hybrid quantum-classical Hamiltonian learning algorithm to find the coefficients of the Pauli operator components of the Hamiltonian. Its main subroutine is the practical log-partition function estimation algorithm, which is based on the minimization of the free energy of the system. Concretely, we devise a stochastic variational quantum eigensolver (SVQE) to diagonalize the Hamiltonians and then exploit the obtained eigenvalues to compute the free energy's global minimum using convex optimization. Our approach not only avoids the challenge of estimating von Neumann entropy in free energy minimization, but also reduces the quantum resources via importance sampling in Hamiltonian diagonalization, facilitating the implementation of our method on near-term quantum devices. Finally, we demonstrate our approach's validity by conducting numerical experiments with Hamiltonians of interest in quantum many-body physics.

Variational Quantum Singular Value Decomposition

Singular value decomposition is central to many problems in both engineering and scientific fields. Several quantum algorithms have been proposed to determine the singular values and their associated singular vectors of a given matrix. Although these quantum algorithms are promising, the required quantum subroutines and resources are too costly on near-term quantum devices. In this work, we propose a variational quantum algorithm for singular value decomposition (VQSVD). By exploiting the variational principles for singular values and the Ky Fan Theorem, we design a novel loss function such that two quantum neural networks or parameterized quantum circuits could be trained to learn the singular vectors and output the corresponding singular values. We further conduct numerical simulations of the algorithm for singular-value decomposition of random matrices as well as its applications in image compression of handwritten digits. Finally, we discuss the applications of our algorithm in systems of linear equations, least squares estimation, and recommendation systems.

Variational quantum Gibbs state preparation with a truncated Taylor series

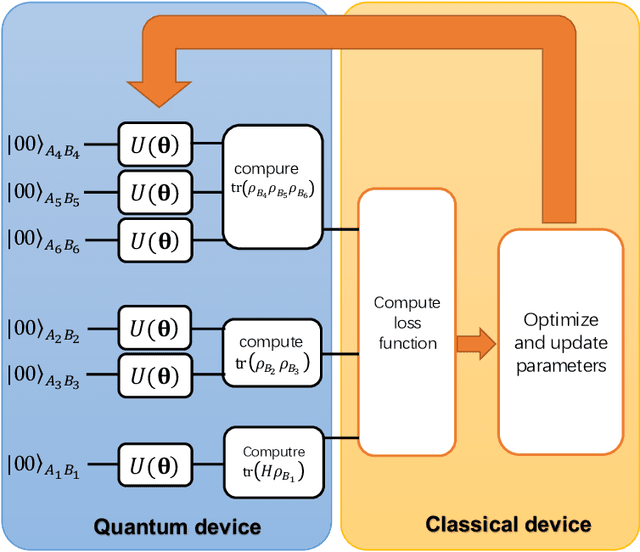
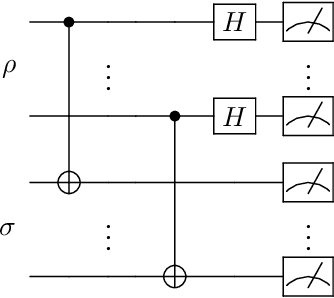
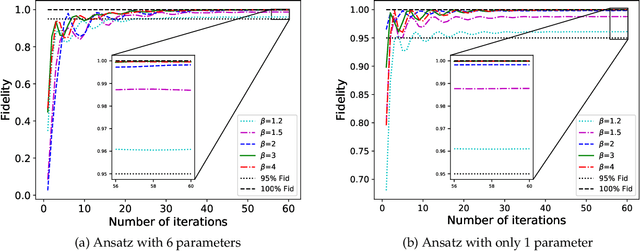
The preparation of quantum Gibbs state is an essential part of quantum computation and has wide-ranging applications in various areas, including quantum simulation, quantum optimization, and quantum machine learning. In this paper, we propose variational hybrid quantum-classical algorithms for quantum Gibbs state preparation. We first utilize a truncated Taylor series to evaluate the free energy and choose the truncated free energy as the loss function. Our protocol then trains the parameterized quantum circuits to learn the desired quantum Gibbs state. Notably, this algorithm can be implemented on near-term quantum computers equipped with parameterized quantum circuits. By performing numerical experiments, we show that shallow parameterized circuits with only one additional qubit can be trained to prepare the Ising chain and spin chain Gibbs states with a fidelity higher than 95%. In particular, for the Ising chain model, we find that a simplified circuit ansatz with only one parameter and one additional qubit can be trained to realize a 99% fidelity in Gibbs state preparation at inverse temperatures larger than 2.

Quantum Data Fitting Algorithm for Non-sparse Matrices

We propose a quantum data fitting algorithm for non-sparse matrices, which is based on the Quantum Singular Value Estimation (QSVE) subroutine and a novel efficient method for recovering the signs of eigenvalues. Our algorithm generalizes the quantum data fitting algorithm of Wiebe, Braun, and Lloyd for sparse and well-conditioned matrices by adding a regularization term to avoid the over-fitting problem, which is a very important problem in machine learning. As a result, the algorithm achieves a sparsity-independent runtime of $O(\kappa^2\sqrt{N}\mathrm{polylog}(N)/(\epsilon\log\kappa))$ for an $N\times N$ dimensional Hermitian matrix $\bm{F}$, where $\kappa$ denotes the condition number of $\bm{F}$ and $\epsilon$ is the precision parameter. This amounts to a polynomial speedup on the dimension of matrices when compared with the classical data fitting algorithms, and a strictly less than quadratic dependence on $\kappa$.