Variational quantum Gibbs state preparation with a truncated Taylor series
Paper and Code
May 18, 2020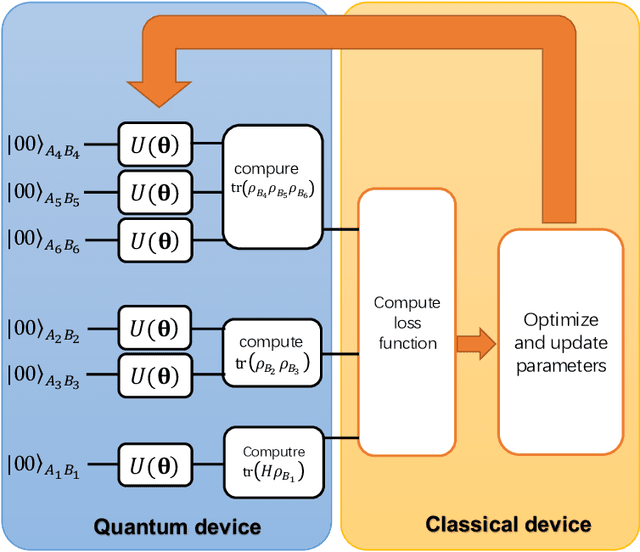
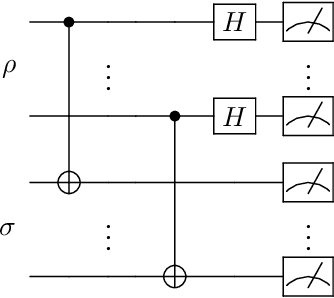

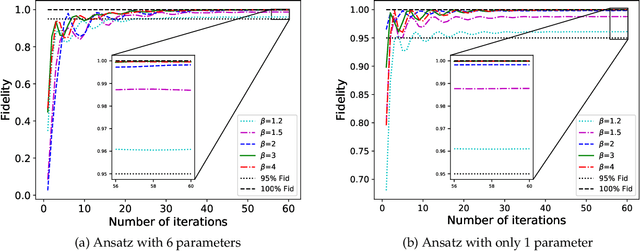
The preparation of quantum Gibbs state is an essential part of quantum computation and has wide-ranging applications in various areas, including quantum simulation, quantum optimization, and quantum machine learning. In this paper, we propose variational hybrid quantum-classical algorithms for quantum Gibbs state preparation. We first utilize a truncated Taylor series to evaluate the free energy and choose the truncated free energy as the loss function. Our protocol then trains the parameterized quantum circuits to learn the desired quantum Gibbs state. Notably, this algorithm can be implemented on near-term quantum computers equipped with parameterized quantum circuits. By performing numerical experiments, we show that shallow parameterized circuits with only one additional qubit can be trained to prepare the Ising chain and spin chain Gibbs states with a fidelity higher than 95%. In particular, for the Ising chain model, we find that a simplified circuit ansatz with only one parameter and one additional qubit can be trained to realize a 99% fidelity in Gibbs state preparation at inverse temperatures larger than 2.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge