Guangxi Li
SAU: A Dual-Branch Network to Enhance Long-Tailed Recognition via Generative Models
Aug 29, 2024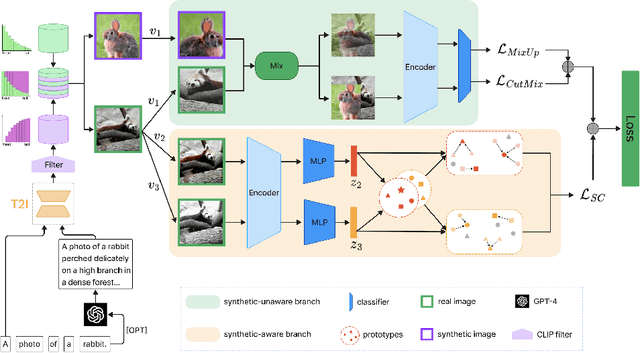
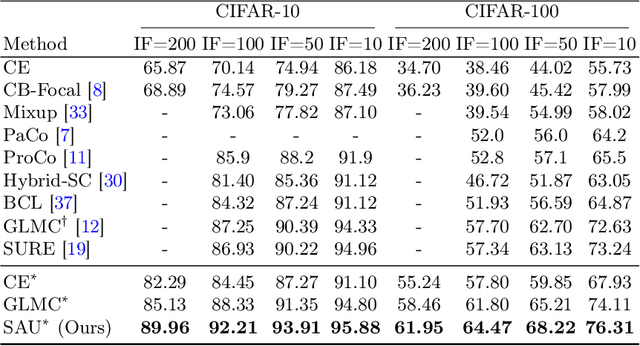
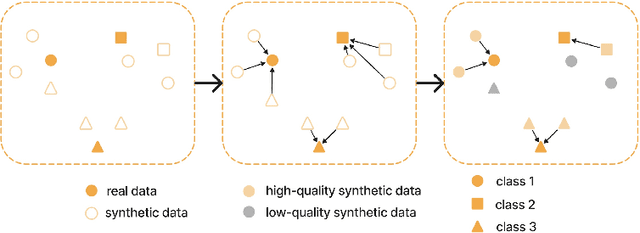
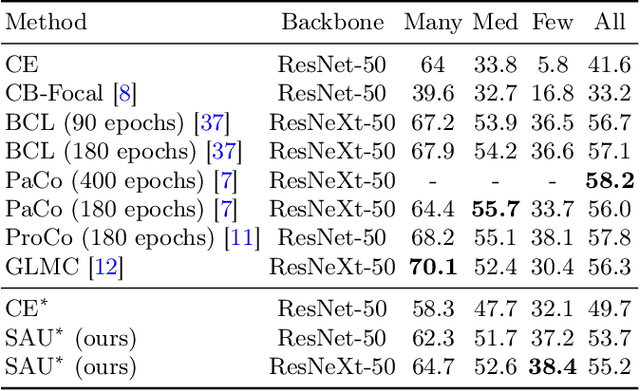
Abstract:Long-tailed distributions in image recognition pose a considerable challenge due to the severe imbalance between a few dominant classes with numerous examples and many minority classes with few samples. Recently, the use of large generative models to create synthetic data for image classification has been realized, but utilizing synthetic data to address the challenge of long-tailed recognition remains relatively unexplored. In this work, we proposed the use of synthetic data as a complement to long-tailed datasets to eliminate the impact of data imbalance. To tackle this real-synthetic mixed dataset, we designed a two-branch model that contains Synthetic-Aware and Unaware branches (SAU). The core ideas are (1) a synthetic-unaware branch for classification that mixes real and synthetic data and treats all data equally without distinguishing between them. (2) A synthetic-aware branch for improving the robustness of the feature extractor by distinguishing between real and synthetic data and learning their discrepancies. Extensive experimental results demonstrate that our method can improve the accuracy of long-tailed image recognition. Notably, our approach achieves state-of-the-art Top-1 accuracy and significantly surpasses other methods on CIFAR-10-LT and CIFAR-100-LT datasets across various imbalance factors. Our code is available at https://github.com/lgX1123/gm4lt.
JointViT: Modeling Oxygen Saturation Levels with Joint Supervision on Long-Tailed OCTA
Apr 18, 2024Abstract:The oxygen saturation level in the blood (SaO2) is crucial for health, particularly in relation to sleep-related breathing disorders. However, continuous monitoring of SaO2 is time-consuming and highly variable depending on patients' conditions. Recently, optical coherence tomography angiography (OCTA) has shown promising development in rapidly and effectively screening eye-related lesions, offering the potential for diagnosing sleep-related disorders. To bridge this gap, our paper presents three key contributions. Firstly, we propose JointViT, a novel model based on the Vision Transformer architecture, incorporating a joint loss function for supervision. Secondly, we introduce a balancing augmentation technique during data preprocessing to improve the model's performance, particularly on the long-tail distribution within the OCTA dataset. Lastly, through comprehensive experiments on the OCTA dataset, our proposed method significantly outperforms other state-of-the-art methods, achieving improvements of up to 12.28% in overall accuracy. This advancement lays the groundwork for the future utilization of OCTA in diagnosing sleep-related disorders. See project website https://steve-zeyu-zhang.github.io/JointViT
Concentration of Data Encoding in Parameterized Quantum Circuits
Jun 16, 2022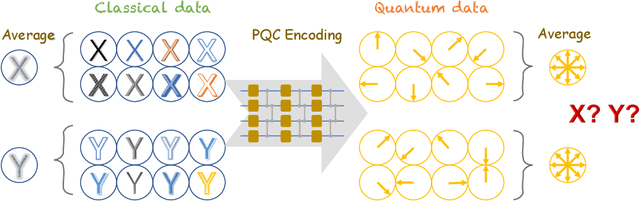

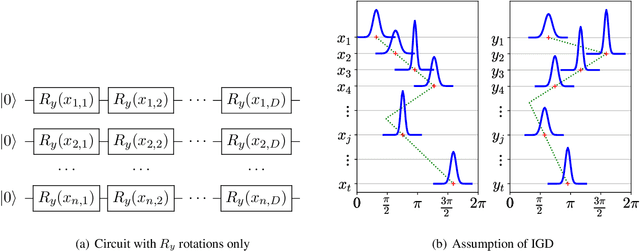
Abstract:Variational quantum algorithms have been acknowledged as a leading strategy to realize near-term quantum advantages in meaningful tasks, including machine learning and combinatorial optimization. When applied to tasks involving classical data, such algorithms generally begin with quantum circuits for data encoding and then train quantum neural networks (QNNs) to minimize target functions. Although QNNs have been widely studied to improve these algorithms' performance on practical tasks, there is a gap in systematically understanding the influence of data encoding on the eventual performance. In this paper, we make progress in filling this gap by considering the common data encoding strategies based on parameterized quantum circuits. We prove that, under reasonable assumptions, the distance between the average encoded state and the maximally mixed state could be explicitly upper-bounded with respect to the width and depth of the encoding circuit. This result in particular implies that the average encoded state will concentrate on the maximally mixed state at an exponential speed on depth. Such concentration seriously limits the capabilities of quantum classifiers, and strictly restricts the distinguishability of encoded states from a quantum information perspective. We further support our findings by numerically verifying these results on both synthetic and public data sets. Our results highlight the significance of quantum data encoding in machine learning tasks and may shed light on future encoding strategies.
Quantum Self-Attention Neural Networks for Text Classification
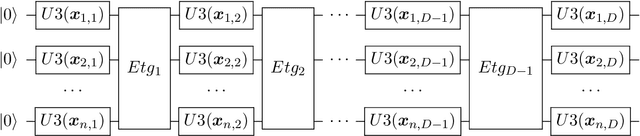
May 11, 2022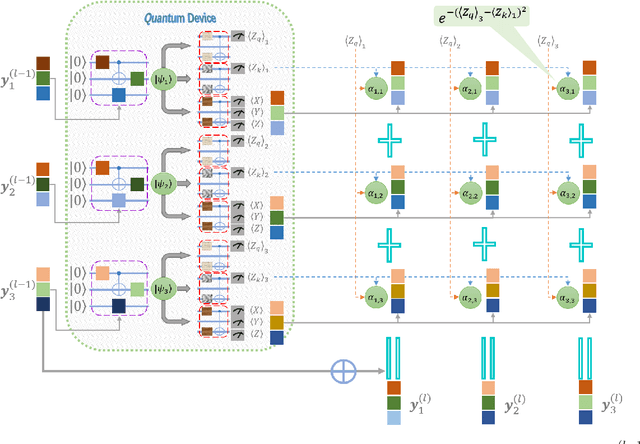

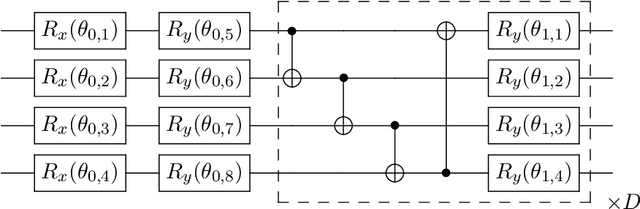

Abstract:An emerging direction of quantum computing is to establish meaningful quantum applications in various fields of artificial intelligence, including natural language processing (NLP). Although some efforts based on syntactic analysis have opened the door to research in Quantum NLP (QNLP), limitations such as heavy syntactic preprocessing and syntax-dependent network architecture make them impracticable on larger and real-world data sets. In this paper, we propose a new simple network architecture, called the quantum self-attention neural network (QSANN), which can make up for these limitations. Specifically, we introduce the self-attention mechanism into quantum neural networks and then utilize a Gaussian projected quantum self-attention serving as a sensible quantum version of self-attention. As a result, QSANN is effective and scalable on larger data sets and has the desirable property of being implementable on near-term quantum devices. In particular, our QSANN outperforms the best existing QNLP model based on syntactic analysis as well as a simple classical self-attention neural network in numerical experiments of text classification tasks on public data sets. We further show that our method exhibits robustness to low-level quantum noises.
A Hybrid Quantum-Classical Hamiltonian Learning Algorithm
Mar 01, 2021



Abstract:Hamiltonian learning is crucial to the certification of quantum devices and quantum simulators. In this paper, we propose a hybrid quantum-classical Hamiltonian learning algorithm to find the coefficients of the Pauli operator components of the Hamiltonian. Its main subroutine is the practical log-partition function estimation algorithm, which is based on the minimization of the free energy of the system. Concretely, we devise a stochastic variational quantum eigensolver (SVQE) to diagonalize the Hamiltonians and then exploit the obtained eigenvalues to compute the free energy's global minimum using convex optimization. Our approach not only avoids the challenge of estimating von Neumann entropy in free energy minimization, but also reduces the quantum resources via importance sampling in Hamiltonian diagonalization, facilitating the implementation of our method on near-term quantum devices. Finally, we demonstrate our approach's validity by conducting numerical experiments with Hamiltonians of interest in quantum many-body physics.
VSQL: Variational Shadow Quantum Learning for Classification
Dec 15, 2020



Abstract:Classification of quantum data is essential for quantum machine learning and near-term quantum technologies. In this paper, we propose a new hybrid quantum-classical framework for supervised quantum learning, which we call Variational Shadow Quantum Learning (VSQL). Our method in particular utilizes the classical shadows of quantum data, which fundamentally represent the side information of quantum data with respect to certain physical observables. Specifically, we first use variational shadow quantum circuits to extract classical features in a convolution way and then utilize a fully-connected neural network to complete the classification task. We show that this method could sharply reduce the number of parameters and thus better facilitate quantum circuit training. Simultaneously, less noise will be introduced since fewer quantum gates are employed in such shadow circuits. Moreover, we show that the Barren Plateau issue, a significant gradient vanishing problem in quantum machine learning, could be avoided in VSQL. Finally, we demonstrate the efficiency of VSQL in quantum classification via numerical experiments on the classification of quantum states and the recognition of multi-labeled handwritten digits. In particular, our VSQL approach outperforms existing variational quantum classifiers in the test accuracy in the binary case of handwritten digit recognition and notably requires much fewer parameters.
Block-term Tensor Neural Networks
Oct 10, 2020



Abstract:Deep neural networks (DNNs) have achieved outstanding performance in a wide range of applications, e.g., image classification, natural language processing, etc. Despite the good performance, the huge number of parameters in DNNs brings challenges to efficient training of DNNs and also their deployment in low-end devices with limited computing resources. In this paper, we explore the correlations in the weight matrices, and approximate the weight matrices with the low-rank block-term tensors. We name the new corresponding structure as block-term tensor layers (BT-layers), which can be easily adapted to neural network models, such as CNNs and RNNs. In particular, the inputs and the outputs in BT-layers are reshaped into low-dimensional high-order tensors with a similar or improved representation power. Sufficient experiments have demonstrated that BT-layers in CNNs and RNNs can achieve a very large compression ratio on the number of parameters while preserving or improving the representation power of the original DNNs.
* 12 pages, 15 figures
Variational quantum Gibbs state preparation with a truncated Taylor series
May 18, 2020



Abstract:The preparation of quantum Gibbs state is an essential part of quantum computation and has wide-ranging applications in various areas, including quantum simulation, quantum optimization, and quantum machine learning. In this paper, we propose variational hybrid quantum-classical algorithms for quantum Gibbs state preparation. We first utilize a truncated Taylor series to evaluate the free energy and choose the truncated free energy as the loss function. Our protocol then trains the parameterized quantum circuits to learn the desired quantum Gibbs state. Notably, this algorithm can be implemented on near-term quantum computers equipped with parameterized quantum circuits. By performing numerical experiments, we show that shallow parameterized circuits with only one additional qubit can be trained to prepare the Ising chain and spin chain Gibbs states with a fidelity higher than 95%. In particular, for the Ising chain model, we find that a simplified circuit ansatz with only one parameter and one additional qubit can be trained to realize a 99% fidelity in Gibbs state preparation at inverse temperatures larger than 2.
Quantum Data Fitting Algorithm for Non-sparse Matrices
Jul 16, 2019
Abstract:We propose a quantum data fitting algorithm for non-sparse matrices, which is based on the Quantum Singular Value Estimation (QSVE) subroutine and a novel efficient method for recovering the signs of eigenvalues. Our algorithm generalizes the quantum data fitting algorithm of Wiebe, Braun, and Lloyd for sparse and well-conditioned matrices by adding a regularization term to avoid the over-fitting problem, which is a very important problem in machine learning. As a result, the algorithm achieves a sparsity-independent runtime of $O(\kappa^2\sqrt{N}\mathrm{polylog}(N)/(\epsilon\log\kappa))$ for an $N\times N$ dimensional Hermitian matrix $\bm{F}$, where $\kappa$ denotes the condition number of $\bm{F}$ and $\epsilon$ is the precision parameter. This amounts to a polynomial speedup on the dimension of matrices when compared with the classical data fitting algorithms, and a strictly less than quadratic dependence on $\kappa$.
Learning Compact Recurrent Neural Networks with Block-Term Tensor Decomposition
May 11, 2018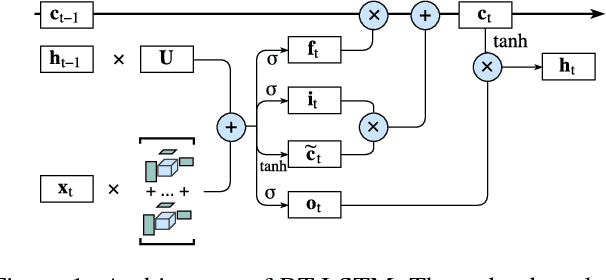
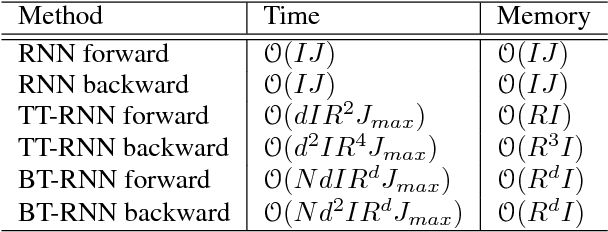
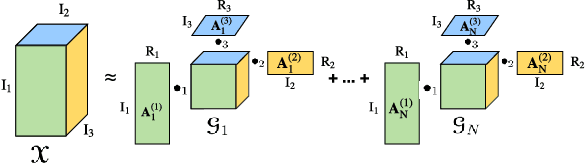

Abstract:Recurrent Neural Networks (RNNs) are powerful sequence modeling tools. However, when dealing with high dimensional inputs, the training of RNNs becomes computational expensive due to the large number of model parameters. This hinders RNNs from solving many important computer vision tasks, such as Action Recognition in Videos and Image Captioning. To overcome this problem, we propose a compact and flexible structure, namely Block-Term tensor decomposition, which greatly reduces the parameters of RNNs and improves their training efficiency. Compared with alternative low-rank approximations, such as tensor-train RNN (TT-RNN), our method, Block-Term RNN (BT-RNN), is not only more concise (when using the same rank), but also able to attain a better approximation to the original RNNs with much fewer parameters. On three challenging tasks, including Action Recognition in Videos, Image Captioning and Image Generation, BT-RNN outperforms TT-RNN and the standard RNN in terms of both prediction accuracy and convergence rate. Specifically, BT-LSTM utilizes 17,388 times fewer parameters than the standard LSTM to achieve an accuracy improvement over 15.6\% in the Action Recognition task on the UCF11 dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge