Concentration of Data Encoding in Parameterized Quantum Circuits

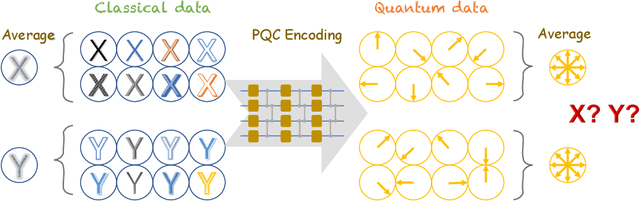
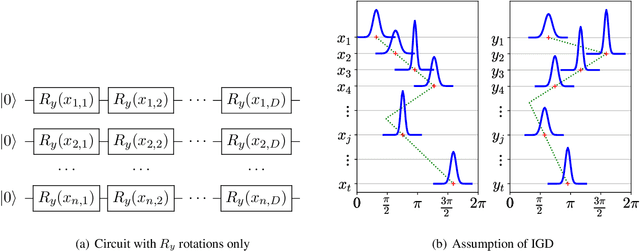
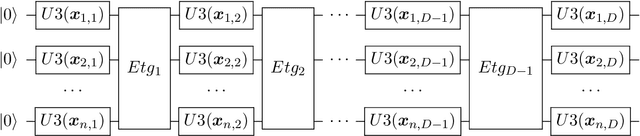
Variational quantum algorithms have been acknowledged as a leading strategy to realize near-term quantum advantages in meaningful tasks, including machine learning and combinatorial optimization. When applied to tasks involving classical data, such algorithms generally begin with quantum circuits for data encoding and then train quantum neural networks (QNNs) to minimize target functions. Although QNNs have been widely studied to improve these algorithms' performance on practical tasks, there is a gap in systematically understanding the influence of data encoding on the eventual performance. In this paper, we make progress in filling this gap by considering the common data encoding strategies based on parameterized quantum circuits. We prove that, under reasonable assumptions, the distance between the average encoded state and the maximally mixed state could be explicitly upper-bounded with respect to the width and depth of the encoding circuit. This result in particular implies that the average encoded state will concentrate on the maximally mixed state at an exponential speed on depth. Such concentration seriously limits the capabilities of quantum classifiers, and strictly restricts the distinguishability of encoded states from a quantum information perspective. We further support our findings by numerically verifying these results on both synthetic and public data sets. Our results highlight the significance of quantum data encoding in machine learning tasks and may shed light on future encoding strategies.

Quantum Self-Attention Neural Networks for Text Classification

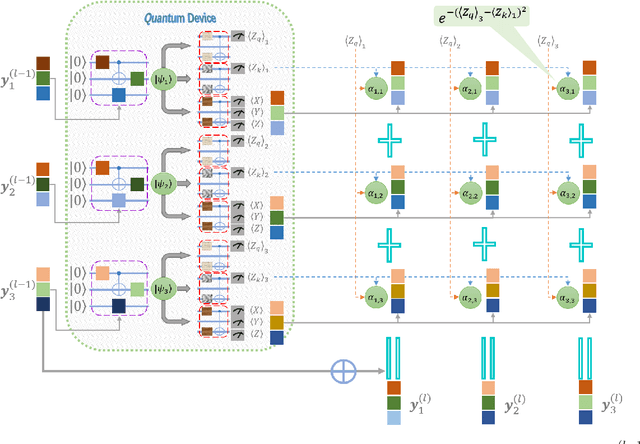
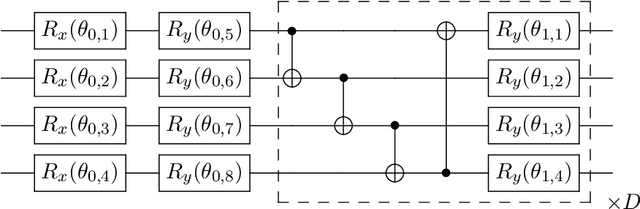
An emerging direction of quantum computing is to establish meaningful quantum applications in various fields of artificial intelligence, including natural language processing (NLP). Although some efforts based on syntactic analysis have opened the door to research in Quantum NLP (QNLP), limitations such as heavy syntactic preprocessing and syntax-dependent network architecture make them impracticable on larger and real-world data sets. In this paper, we propose a new simple network architecture, called the quantum self-attention neural network (QSANN), which can make up for these limitations. Specifically, we introduce the self-attention mechanism into quantum neural networks and then utilize a Gaussian projected quantum self-attention serving as a sensible quantum version of self-attention. As a result, QSANN is effective and scalable on larger data sets and has the desirable property of being implementable on near-term quantum devices. In particular, our QSANN outperforms the best existing QNLP model based on syntactic analysis as well as a simple classical self-attention neural network in numerical experiments of text classification tasks on public data sets. We further show that our method exhibits robustness to low-level quantum noises.

Optimal quantum dataset for learning a unitary transformation

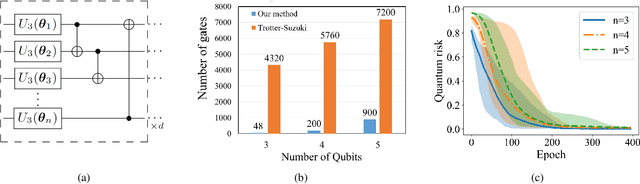
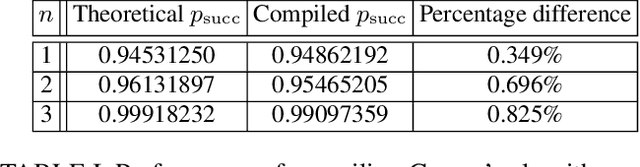
Unitary transformations formulate the time evolution of quantum states. How to learn a unitary transformation efficiently is a fundamental problem in quantum machine learning. The most natural and leading strategy is to train a quantum machine learning model based on a quantum dataset. Although presence of more training data results in better models, using too much data reduces the efficiency of training. In this work, we solve the problem on the minimum size of sufficient quantum datasets for learning a unitary transformation exactly, which reveals the power and limitation of quantum data. First, we prove that the minimum size of dataset with pure states is $2^n$ for learning an $n$-qubit unitary transformation. To fully explore the capability of quantum data, we introduce a quantum dataset consisting of $n+1$ mixed states that are sufficient for exact training. The main idea is to simplify the structure utilizing decoupling, which leads to an exponential improvement on the size over the datasets with pure states. Furthermore, we show that the size of quantum dataset with mixed states can be reduced to a constant, which yields an optimal quantum dataset for learning a unitary. We showcase the applications of our results in oracle compiling and Hamiltonian simulation. Notably, to accurately simulate a 3-qubit one-dimensional nearest-neighbor Heisenberg model, our circuit only uses $48$ elementary quantum gates, which is significantly less than $4320$ gates in the circuit constructed by the Trotter-Suzuki product formula.

LOCCNet: a machine learning framework for distributed quantum information processing

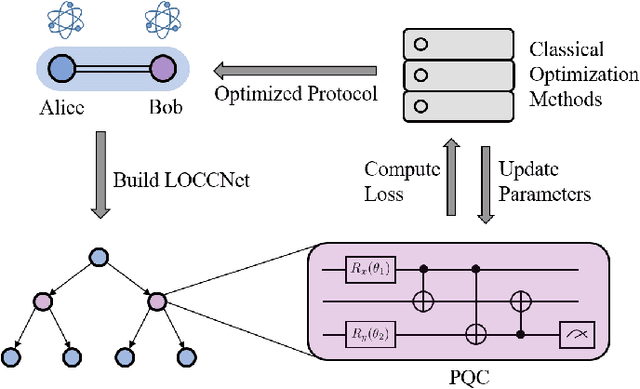
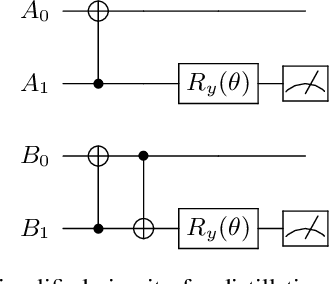
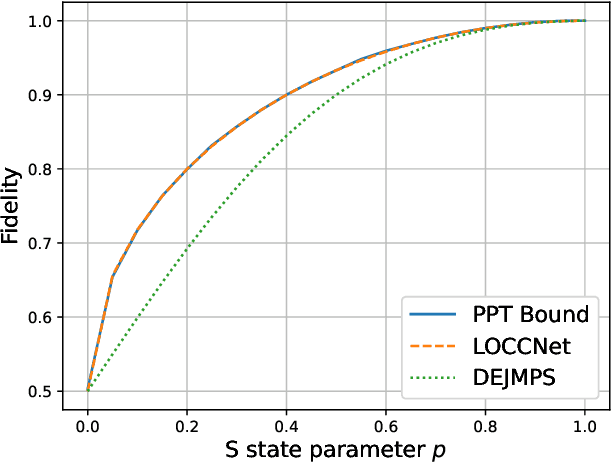
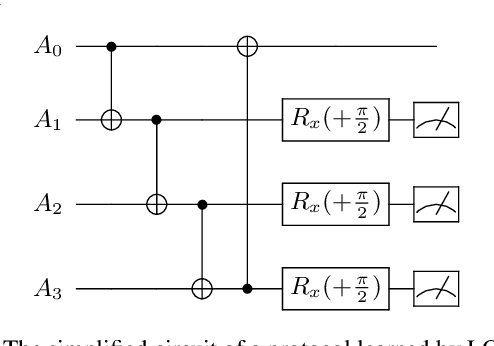
Distributed quantum information processing is essential for building quantum networks and enabling more extensive quantum computations. In this regime, several spatially separated parties share a multipartite quantum system, and the most natural set of operations are Local Operations and Classical Communication (LOCC). As a pivotal part in quantum information theory and practice, LOCC has led to many vital protocols such as quantum teleportation. However, designing practical LOCC protocols is challenging due to LOCC's intractable structure and limitations set by near-term quantum devices. Here we introduce LOCCNet, a machine learning framework facilitating protocol design and optimization for distributed quantum information processing tasks. As applications, we explore various quantum information tasks such as entanglement distillation, quantum state discrimination, and quantum channel simulation. We discover novel protocols with evident improvements, in particular, for entanglement distillation with quantum states of interest in quantum information. Our approach opens up new opportunities for exploring entanglement and its applications with machine learning, which will potentially sharpen our understanding of the power and limitations of LOCC.