Ruilin Ye
Concentration of Data Encoding in Parameterized Quantum Circuits
Jun 16, 2022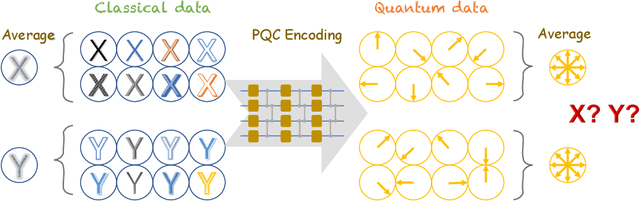

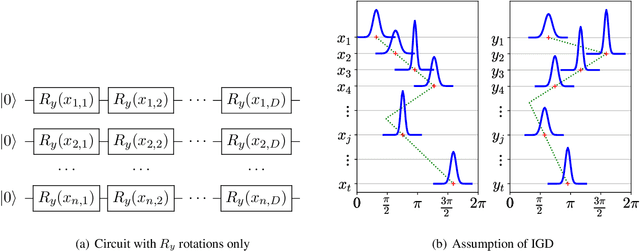
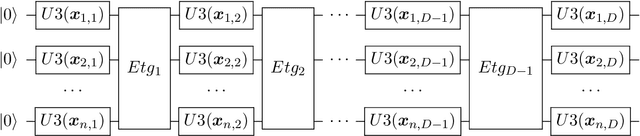
Abstract:Variational quantum algorithms have been acknowledged as a leading strategy to realize near-term quantum advantages in meaningful tasks, including machine learning and combinatorial optimization. When applied to tasks involving classical data, such algorithms generally begin with quantum circuits for data encoding and then train quantum neural networks (QNNs) to minimize target functions. Although QNNs have been widely studied to improve these algorithms' performance on practical tasks, there is a gap in systematically understanding the influence of data encoding on the eventual performance. In this paper, we make progress in filling this gap by considering the common data encoding strategies based on parameterized quantum circuits. We prove that, under reasonable assumptions, the distance between the average encoded state and the maximally mixed state could be explicitly upper-bounded with respect to the width and depth of the encoding circuit. This result in particular implies that the average encoded state will concentrate on the maximally mixed state at an exponential speed on depth. Such concentration seriously limits the capabilities of quantum classifiers, and strictly restricts the distinguishability of encoded states from a quantum information perspective. We further support our findings by numerically verifying these results on both synthetic and public data sets. Our results highlight the significance of quantum data encoding in machine learning tasks and may shed light on future encoding strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge