Pseudo-Physics-Informed Neural Operators: Enhancing Operator Learning from Limited Data

Neural operators have shown great potential in surrogate modeling. However, training a well-performing neural operator typically requires a substantial amount of data, which can pose a major challenge in complex applications. In such scenarios, detailed physical knowledge can be unavailable or difficult to obtain, and collecting extensive data is often prohibitively expensive. To mitigate this challenge, we propose the Pseudo Physics-Informed Neural Operator (PPI-NO) framework. PPI-NO constructs a surrogate physics system for the target system using partial differential equations (PDEs) derived from simple, rudimentary physics principles, such as basic differential operators. This surrogate system is coupled with a neural operator model, using an alternating update and learning process to iteratively enhance the model's predictive power. While the physics derived via PPI-NO may not mirror the ground-truth underlying physical laws -- hence the term ``pseudo physics'' -- this approach significantly improves the accuracy of standard operator learning models in data-scarce scenarios, which is evidenced by extensive evaluations across five benchmark tasks and a fatigue modeling application.

Arbitrarily-Conditioned Multi-Functional Diffusion for Multi-Physics Emulation

Modern physics simulation often involves multiple functions of interests, and traditional numerical approaches are known to be complex and computationally costly. While machine learning-based surrogate models can offer significant cost reductions, most focus on a single task, such as forward prediction, and typically lack uncertainty quantification -- an essential component in many applications. To overcome these limitations, we propose Arbitrarily-Conditioned Multi-Functional Diffusion (ACMFD), a versatile probabilistic surrogate model for multi-physics emulation. ACMFD can perform a wide range of tasks within a single framework, including forward prediction, various inverse problems, and simulating data for entire systems or subsets of quantities conditioned on others. Specifically, we extend the standard Denoising Diffusion Probabilistic Model (DDPM) for multi-functional generation by modeling noise as Gaussian processes (GP). We then introduce an innovative denoising loss. The training involves randomly sampling the conditioned part and fitting the corresponding predicted noise to zero, enabling ACMFD to flexibly generate function values conditioned on any other functions or quantities. To enable efficient training and sampling, and to flexibly handle irregularly sampled data, we use GPs to interpolate function samples onto a grid, inducing a Kronecker product structure for efficient computation. We demonstrate the advantages of ACMFD across several fundamental multi-physics systems.

Toward Efficient Kernel-Based Solvers for Nonlinear PDEs

This paper introduces a novel kernel learning framework toward efficiently solving nonlinear partial differential equations (PDEs). In contrast to the state-of-the-art kernel solver that embeds differential operators within kernels, posing challenges with a large number of collocation points, our approach eliminates these operators from the kernel. We model the solution using a standard kernel interpolation form and differentiate the interpolant to compute the derivatives. Our framework obviates the need for complex Gram matrix construction between solutions and their derivatives, allowing for a straightforward implementation and scalable computation. As an instance, we allocate the collocation points on a grid and adopt a product kernel, which yields a Kronecker product structure in the interpolation. This structure enables us to avoid computing the full Gram matrix, reducing costs and scaling efficiently to a large number of collocation points. We provide a proof of the convergence and rate analysis of our method under appropriate regularity assumptions. In numerical experiments, we demonstrate the advantages of our method in solving several benchmark PDEs.

HyResPINNs: Adaptive Hybrid Residual Networks for Learning Optimal Combinations of Neural and RBF Components for Physics-Informed Modeling

Physics-informed neural networks (PINNs) are an increasingly popular class of techniques for the numerical solution of partial differential equations (PDEs), where neural networks are trained using loss functions regularized by relevant PDE terms to enforce physical constraints. We present a new class of PINNs called HyResPINNs, which augment traditional PINNs with adaptive hybrid residual blocks that combine the outputs of a standard neural network and a radial basis function (RBF) network. A key feature of our method is the inclusion of adaptive combination parameters within each residual block, which dynamically learn to weigh the contributions of the neural network and RBF network outputs. Additionally, adaptive connections between residual blocks allow for flexible information flow throughout the network. We show that HyResPINNs are more robust to training point locations and neural network architectures than traditional PINNs. Moreover, HyResPINNs offer orders of magnitude greater accuracy than competing methods on certain problems, with only modest increases in training costs. We demonstrate the strengths of our approach on challenging PDEs, including the Allen-Cahn equation and the Darcy-Flow equation. Our results suggest that HyResPINNs effectively bridge the gap between traditional numerical methods and modern machine learning-based solvers.

Fourier PINNs: From Strong Boundary Conditions to Adaptive Fourier Bases

Interest is rising in Physics-Informed Neural Networks (PINNs) as a mesh-free alternative to traditional numerical solvers for partial differential equations (PDEs). However, PINNs often struggle to learn high-frequency and multi-scale target solutions. To tackle this problem, we first study a strong Boundary Condition (BC) version of PINNs for Dirichlet BCs and observe a consistent decline in relative error compared to the standard PINNs. We then perform a theoretical analysis based on the Fourier transform and convolution theorem. We find that strong BC PINNs can better learn the amplitudes of high-frequency components of the target solutions. However, constructing the architecture for strong BC PINNs is difficult for many BCs and domain geometries. Enlightened by our theoretical analysis, we propose Fourier PINNs -- a simple, general, yet powerful method that augments PINNs with pre-specified, dense Fourier bases. Our proposed architecture likewise learns high-frequency components better but places no restrictions on the particular BCs or problem domains. We develop an adaptive learning and basis selection algorithm via alternating neural net basis optimization, Fourier and neural net basis coefficient estimation, and coefficient truncation. This scheme can flexibly identify the significant frequencies while weakening the nominal frequencies to better capture the target solution's power spectrum. We show the advantage of our approach through a set of systematic experiments.

Kernel Neural Operators (KNOs) for Scalable, Memory-efficient, Geometrically-flexible Operator Learning

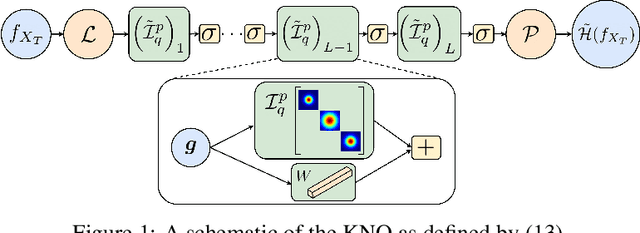
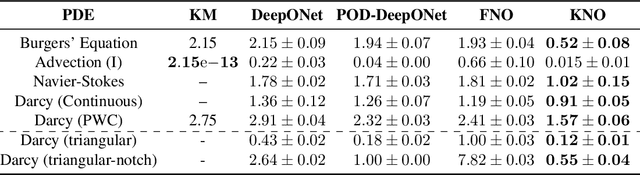
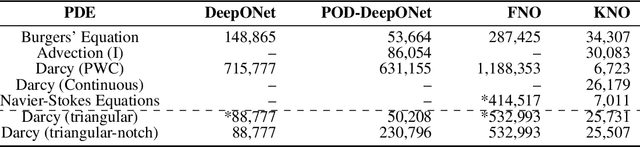
This paper introduces the Kernel Neural Operator (KNO), a novel operator learning technique that uses deep kernel-based integral operators in conjunction with quadrature for function-space approximation of operators (maps from functions to functions). KNOs use parameterized, closed-form, finitely-smooth, and compactly-supported kernels with trainable sparsity parameters within the integral operators to significantly reduce the number of parameters that must be learned relative to existing neural operators. Moreover, the use of quadrature for numerical integration endows the KNO with geometric flexibility that enables operator learning on irregular geometries. Numerical results demonstrate that on existing benchmarks the training and test accuracy of KNOs is higher than popular operator learning techniques while using at least an order of magnitude fewer trainable parameters. KNOs thus represent a new paradigm of low-memory, geometrically-flexible, deep operator learning, while retaining the implementation simplicity and transparency of traditional kernel methods from both scientific computing and machine learning.

Complexity-Aware Deep Symbolic Regression with Robust Risk-Seeking Policy Gradients

This paper proposes a novel deep symbolic regression approach to enhance the robustness and interpretability of data-driven mathematical expression discovery. Despite the success of the state-of-the-art method, DSR, it is built on recurrent neural networks, purely guided by data fitness, and potentially meet tail barriers, which can zero out the policy gradient and cause inefficient model updates. To overcome these limitations, we use transformers in conjunction with breadth-first-search to improve the learning performance. We use Bayesian information criterion (BIC) as the reward function to explicitly account for the expression complexity and optimize the trade-off between interpretability and data fitness. We propose a modified risk-seeking policy that not only ensures the unbiasness of the gradient, but also removes the tail barriers, thus ensuring effective updates from top performers. Through a series of benchmarks and systematic experiments, we demonstrate the advantages of our approach.

Polynomial-Augmented Neural Networks (PANNs) with Weak Orthogonality Constraints for Enhanced Function and PDE Approximation

We present polynomial-augmented neural networks (PANNs), a novel machine learning architecture that combines deep neural networks (DNNs) with a polynomial approximant. PANNs combine the strengths of DNNs (flexibility and efficiency in higher-dimensional approximation) with those of polynomial approximation (rapid convergence rates for smooth functions). To aid in both stable training and enhanced accuracy over a variety of problems, we present (1) a family of orthogonality constraints that impose mutual orthogonality between the polynomial and the DNN within a PANN; (2) a simple basis pruning approach to combat the curse of dimensionality introduced by the polynomial component; and (3) an adaptation of a polynomial preconditioning strategy to both DNNs and polynomials. We test the resulting architecture for its polynomial reproduction properties, ability to approximate both smooth functions and functions of limited smoothness, and as a method for the solution of partial differential equations (PDEs). Through these experiments, we demonstrate that PANNs offer superior approximation properties to DNNs for both regression and the numerical solution of PDEs, while also offering enhanced accuracy over both polynomial and DNN-based regression (each) when regressing functions with limited smoothness.

ElastoGen: 4D Generative Elastodynamics

We present ElastoGen, a knowledge-driven model that generates physically accurate and coherent 4D elastodynamics. Instead of relying on petabyte-scale data-driven learning, ElastoGen leverages the principles of physics-in-the-loop and learns from established physical knowledge, such as partial differential equations and their numerical solutions. The core idea of ElastoGen is converting the global differential operator, corresponding to the nonlinear elastodynamic equations, into iterative local convolution-like operations, which naturally fit modern neural networks. Each network module is specifically designed to support this goal rather than functioning as a black box. As a result, ElastoGen is exceptionally lightweight in terms of both training requirements and network scale. Additionally, due to its alignment with physical procedures, ElastoGen efficiently generates accurate dynamics for a wide range of hyperelastic materials and can be easily integrated with upstream and downstream deep modules to enable end-to-end 4D generation.

Invertible Fourier Neural Operators for Tackling Both Forward and Inverse Problems

Fourier Neural Operator (FNO) is a popular operator learning method, which has demonstrated state-of-the-art performance across many tasks. However, FNO is mainly used in forward prediction, yet a large family of applications rely on solving inverse problems. In this paper, we propose an invertible Fourier Neural Operator (iFNO) that tackles both the forward and inverse problems. We designed a series of invertible Fourier blocks in the latent channel space to share the model parameters, efficiently exchange the information, and mutually regularize the learning for the bi-directional tasks. We integrated a variational auto-encoder to capture the intrinsic structures within the input space and to enable posterior inference so as to overcome challenges of illposedness, data shortage, noises, etc. We developed a three-step process for pre-training and fine tuning for efficient training. The evaluations on five benchmark problems have demonstrated the effectiveness of our approach.