Arbitrarily-Conditioned Multi-Functional Diffusion for Multi-Physics Emulation

Modern physics simulation often involves multiple functions of interests, and traditional numerical approaches are known to be complex and computationally costly. While machine learning-based surrogate models can offer significant cost reductions, most focus on a single task, such as forward prediction, and typically lack uncertainty quantification -- an essential component in many applications. To overcome these limitations, we propose Arbitrarily-Conditioned Multi-Functional Diffusion (ACMFD), a versatile probabilistic surrogate model for multi-physics emulation. ACMFD can perform a wide range of tasks within a single framework, including forward prediction, various inverse problems, and simulating data for entire systems or subsets of quantities conditioned on others. Specifically, we extend the standard Denoising Diffusion Probabilistic Model (DDPM) for multi-functional generation by modeling noise as Gaussian processes (GP). We then introduce an innovative denoising loss. The training involves randomly sampling the conditioned part and fitting the corresponding predicted noise to zero, enabling ACMFD to flexibly generate function values conditioned on any other functions or quantities. To enable efficient training and sampling, and to flexibly handle irregularly sampled data, we use GPs to interpolate function samples onto a grid, inducing a Kronecker product structure for efficient computation. We demonstrate the advantages of ACMFD across several fundamental multi-physics systems.

Toward Efficient Kernel-Based Solvers for Nonlinear PDEs

This paper introduces a novel kernel learning framework toward efficiently solving nonlinear partial differential equations (PDEs). In contrast to the state-of-the-art kernel solver that embeds differential operators within kernels, posing challenges with a large number of collocation points, our approach eliminates these operators from the kernel. We model the solution using a standard kernel interpolation form and differentiate the interpolant to compute the derivatives. Our framework obviates the need for complex Gram matrix construction between solutions and their derivatives, allowing for a straightforward implementation and scalable computation. As an instance, we allocate the collocation points on a grid and adopt a product kernel, which yields a Kronecker product structure in the interpolation. This structure enables us to avoid computing the full Gram matrix, reducing costs and scaling efficiently to a large number of collocation points. We provide a proof of the convergence and rate analysis of our method under appropriate regularity assumptions. In numerical experiments, we demonstrate the advantages of our method in solving several benchmark PDEs.

Invertible Fourier Neural Operators for Tackling Both Forward and Inverse Problems

Fourier Neural Operator (FNO) is a popular operator learning method, which has demonstrated state-of-the-art performance across many tasks. However, FNO is mainly used in forward prediction, yet a large family of applications rely on solving inverse problems. In this paper, we propose an invertible Fourier Neural Operator (iFNO) that tackles both the forward and inverse problems. We designed a series of invertible Fourier blocks in the latent channel space to share the model parameters, efficiently exchange the information, and mutually regularize the learning for the bi-directional tasks. We integrated a variational auto-encoder to capture the intrinsic structures within the input space and to enable posterior inference so as to overcome challenges of illposedness, data shortage, noises, etc. We developed a three-step process for pre-training and fine tuning for efficient training. The evaluations on five benchmark problems have demonstrated the effectiveness of our approach.

Solving High Frequency and Multi-Scale PDEs with Gaussian Processes

Machine learning based solvers have garnered much attention in physical simulation and scientific computing, with a prominent example, physics-informed neural networks (PINNs). However, PINNs often struggle to solve high-frequency and multi-scale PDEs, which can be due to spectral bias during neural network training. To address this problem, we resort to the Gaussian process (GP) framework. To flexibly capture the dominant frequencies, we model the power spectrum of the PDE solution with a student t mixture or Gaussian mixture. We then apply the inverse Fourier transform to obtain the covariance function (according to the Wiener-Khinchin theorem). The covariance derived from the Gaussian mixture spectrum corresponds to the known spectral mixture kernel. We are the first to discover its rationale and effectiveness for PDE solving. Next,we estimate the mixture weights in the log domain, which we show is equivalent to placing a Jeffreys prior. It automatically induces sparsity, prunes excessive frequencies, and adjusts the remaining toward the ground truth. Third, to enable efficient and scalable computation on massive collocation points, which are critical to capture high frequencies, we place the collocation points on a grid, and multiply our covariance function at each input dimension. We use the GP conditional mean to predict the solution and its derivatives so as to fit the boundary condition and the equation itself. As a result, we can derive a Kronecker product structure in the covariance matrix. We use Kronecker product properties and multilinear algebra to greatly promote computational efficiency and scalability, without any low-rank approximations. We show the advantage of our method in systematic experiments.

Equation Discovery with Bayesian Spike-and-Slab Priors and Efficient Kernels

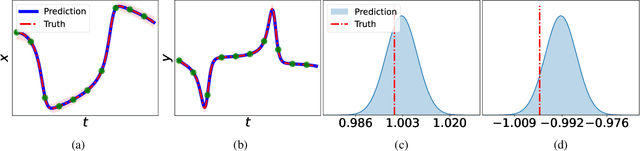
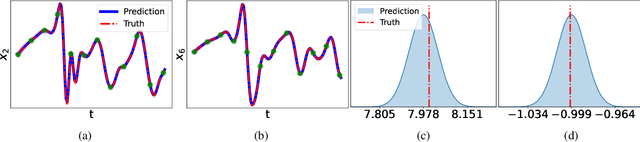
Discovering governing equations from data is important to many scientific and engineering applications. Despite promising successes, existing methods are still challenged by data sparsity as well as noise issues, both of which are ubiquitous in practice. Moreover, state-of-the-art methods lack uncertainty quantification and/or are costly in training. To overcome these limitations, we propose a novel equation discovery method based on Kernel learning and BAyesian Spike-and-Slab priors (KBASS). We use kernel regression to estimate the target function, which is flexible, expressive, and more robust to data sparsity and noises. We combine it with a Bayesian spike-and-slab prior -- an ideal Bayesian sparse distribution -- for effective operator selection and uncertainty quantification. We develop an expectation propagation expectation-maximization (EP-EM) algorithm for efficient posterior inference and function estimation. To overcome the computational challenge of kernel regression, we place the function values on a mesh and induce a Kronecker product construction, and we use tensor algebra methods to enable efficient computation and optimization. We show the significant advantages of KBASS on a list of benchmark ODE and PDE discovery tasks.

A Kernel Approach for PDE Discovery and Operator Learning

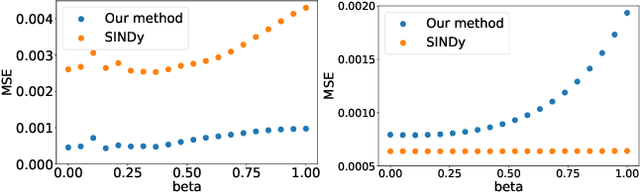
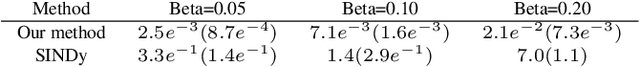
This article presents a three-step framework for learning and solving partial differential equations (PDEs) using kernel methods. Given a training set consisting of pairs of noisy PDE solutions and source/boundary terms on a mesh, kernel smoothing is utilized to denoise the data and approximate derivatives of the solution. This information is then used in a kernel regression model to learn the algebraic form of the PDE. The learned PDE is then used within a kernel based solver to approximate the solution of the PDE with a new source/boundary term, thereby constituting an operator learning framework. The proposed method is mathematically interpretable and amenable to analysis, and convenient to implement. Numerical experiments compare the method to state-of-the-art algorithms and demonstrate its superior performance on small amounts of training data and for PDEs with spatially variable coefficients.

AutoIP: A United Framework to Integrate Physics into Gaussian Processes

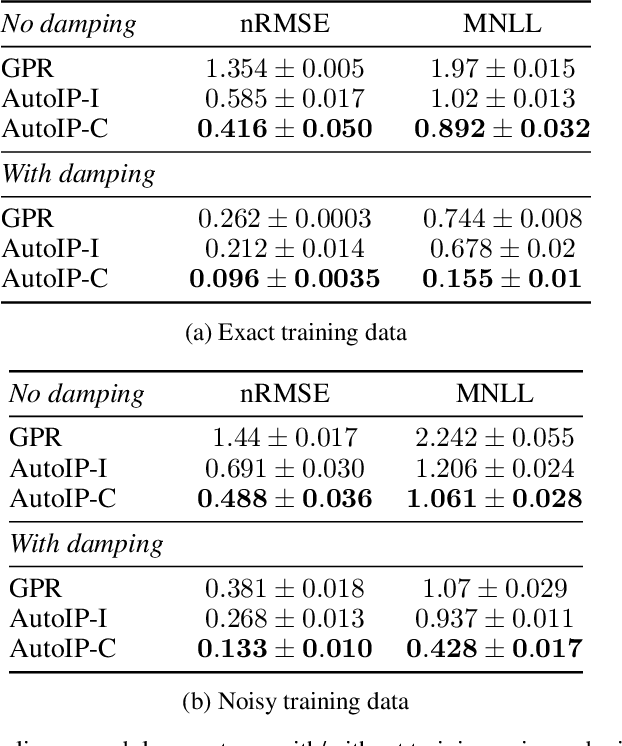
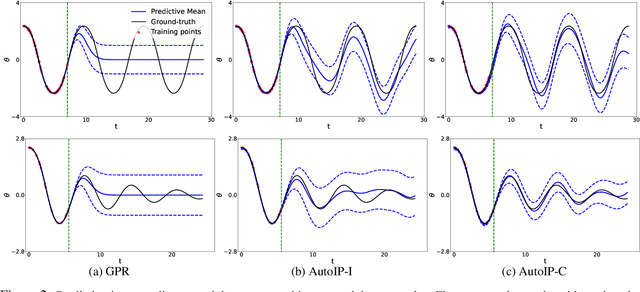
Physics modeling is critical for modern science and engineering applications. From data science perspective, physics knowledge -- often expressed as differential equations -- is valuable in that it is highly complementary to data, and can potentially help overcome data sparsity, noise, inaccuracy, etc. In this work, we propose a simple yet powerful framework that can integrate all kinds of differential equations into Gaussian processes (GPs) to enhance prediction accuracy and uncertainty quantification. These equations can be linear, nonlinear, temporal, time-spatial, complete, incomplete with unknown source terms, etc. Specifically, based on kernel differentiation, we construct a GP prior to jointly sample the values of the target function, equation-related derivatives, and latent source functions from a multivariate Gaussian distribution. The sampled values are fed to two likelihoods -- one is to fit the observations and the other to conform to the equation. We use the whitening trick to evade the strong dependency between the sampled function values and kernel parameters, and develop a stochastic variational learning algorithm. Our method shows improvement upon vanilla GPs in both simulation and several real-world applications, even using rough, incomplete equations.