KATO: Knowledge Alignment and Transfer for Transistor Sizing of Different Design and Technology

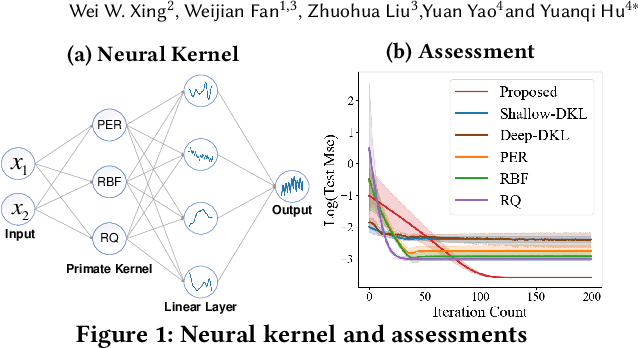
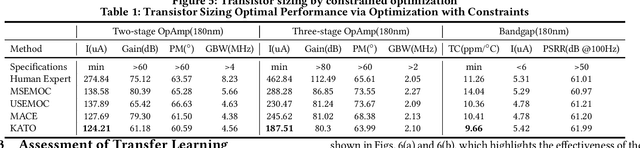
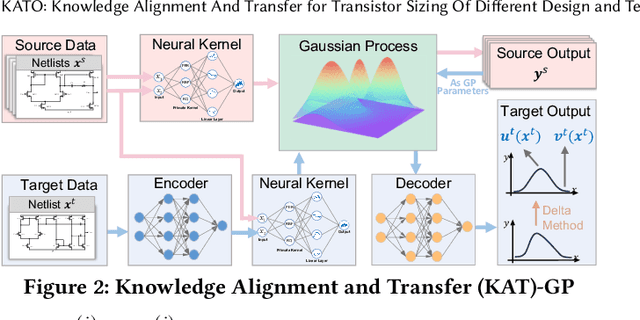
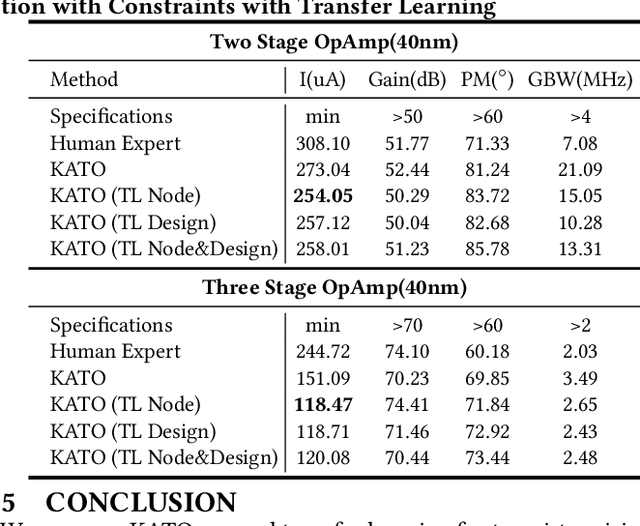
Automatic transistor sizing in circuit design continues to be a formidable challenge. Despite that Bayesian optimization (BO) has achieved significant success, it is circuit-specific, limiting the accumulation and transfer of design knowledge for broader applications. This paper proposes (1) efficient automatic kernel construction, (2) the first transfer learning across different circuits and technology nodes for BO, and (3) a selective transfer learning scheme to ensure only useful knowledge is utilized. These three novel components are integrated into BO with Multi-objective Acquisition Ensemble (MACE) to form Knowledge Alignment and Transfer Optimization (KATO) to deliver state-of-the-art performance: up to 2x simulation reduction and 1.2x design improvement over the baselines.

Equation Discovery with Bayesian Spike-and-Slab Priors and Efficient Kernels

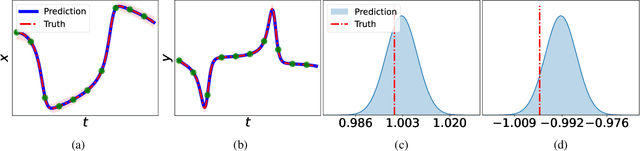
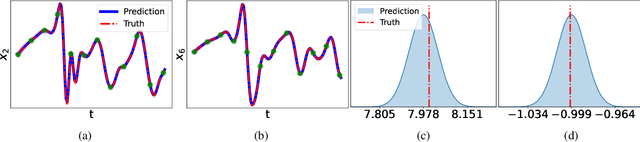
Discovering governing equations from data is important to many scientific and engineering applications. Despite promising successes, existing methods are still challenged by data sparsity as well as noise issues, both of which are ubiquitous in practice. Moreover, state-of-the-art methods lack uncertainty quantification and/or are costly in training. To overcome these limitations, we propose a novel equation discovery method based on Kernel learning and BAyesian Spike-and-Slab priors (KBASS). We use kernel regression to estimate the target function, which is flexible, expressive, and more robust to data sparsity and noises. We combine it with a Bayesian spike-and-slab prior -- an ideal Bayesian sparse distribution -- for effective operator selection and uncertainty quantification. We develop an expectation propagation expectation-maximization (EP-EM) algorithm for efficient posterior inference and function estimation. To overcome the computational challenge of kernel regression, we place the function values on a mesh and induce a Kronecker product construction, and we use tensor algebra methods to enable efficient computation and optimization. We show the significant advantages of KBASS on a list of benchmark ODE and PDE discovery tasks.

Seeking the Yield Barrier: High-Dimensional SRAM Evaluation Through Optimal Manifold

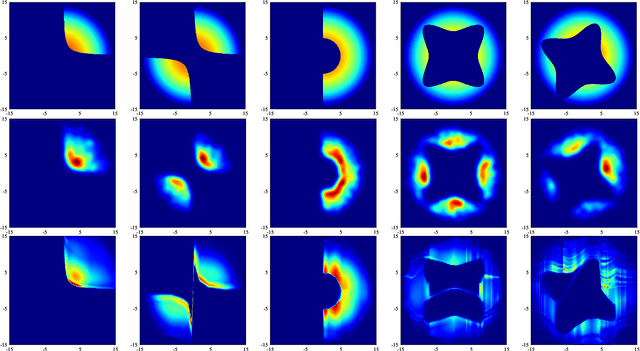
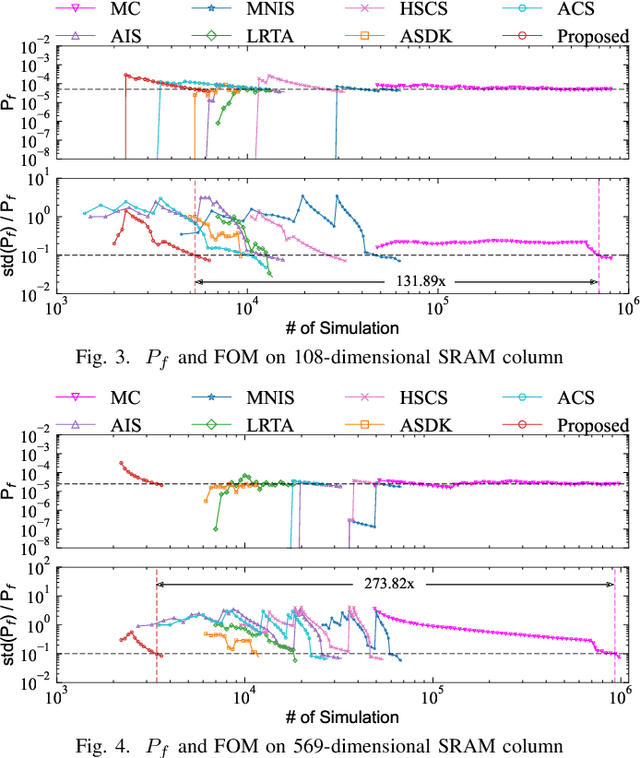
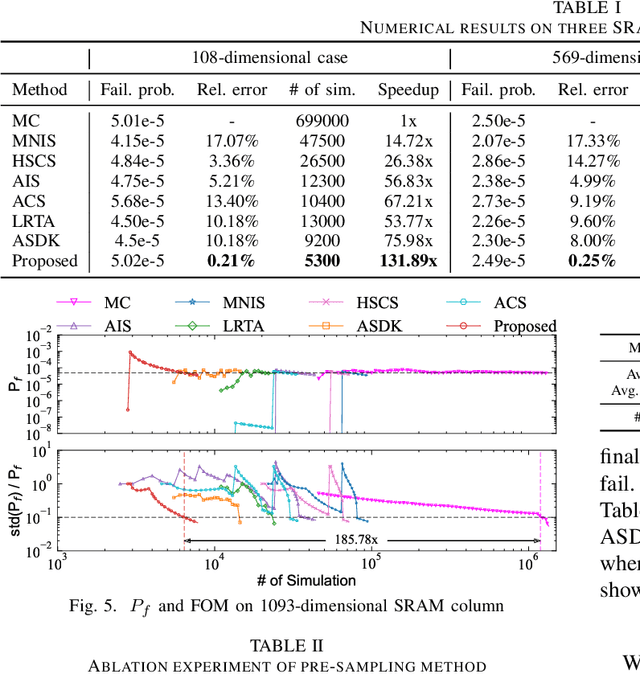
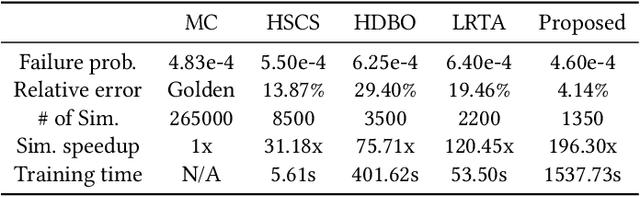
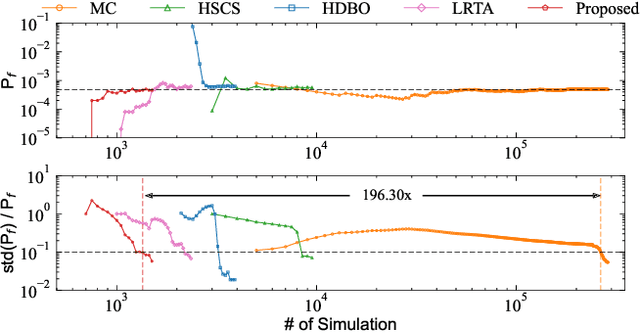
Being able to efficiently obtain an accurate estimate of the failure probability of SRAM components has become a central issue as model circuits shrink their scale to submicrometer with advanced technology nodes. In this work, we revisit the classic norm minimization method. We then generalize it with infinite components and derive the novel optimal manifold concept, which bridges the surrogate-based and importance sampling (IS) yield estimation methods. We then derive a sub-optimal manifold, optimal hypersphere, which leads to an efficient sampling method being aware of the failure boundary called onion sampling. Finally, we use a neural coupling flow (which learns from samples like a surrogate model) as the IS proposal distribution. These combinations give rise to a novel yield estimation method, named Optimal Manifold Important Sampling (OPTIMIS), which keeps the advantages of the surrogate and IS methods to deliver state-of-the-art performance with robustness and consistency, with up to 3.5x in efficiency and 3x in accuracy over the best of SOTA methods in High-dimensional SRAM evaluation.

Differentiable Multi-Fidelity Fusion: Efficient Learning of Physics Simulations with Neural Architecture Search and Transfer Learning

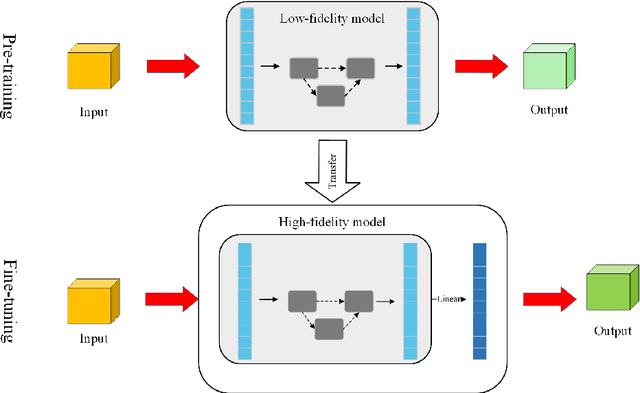
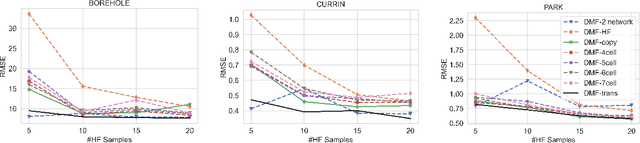
With rapid progress in deep learning, neural networks have been widely used in scientific research and engineering applications as surrogate models. Despite the great success of neural networks in fitting complex systems, two major challenges still remain: i) the lack of generalization on different problems/datasets, and ii) the demand for large amounts of simulation data that are computationally expensive. To resolve these challenges, we propose the differentiable \mf (DMF) model, which leverages neural architecture search (NAS) to automatically search the suitable model architecture for different problems, and transfer learning to transfer the learned knowledge from low-fidelity (fast but inaccurate) data to high-fidelity (slow but accurate) model. Novel and latest machine learning techniques such as hyperparameters search and alternate learning are used to improve the efficiency and robustness of DMF. As a result, DMF can efficiently learn the physics simulations with only a few high-fidelity training samples, and outperform the state-of-the-art methods with a significant margin (with up to 58$\%$ improvement in RMSE) based on a variety of synthetic and practical benchmark problems.

GAR: Generalized Autoregression for Multi-Fidelity Fusion

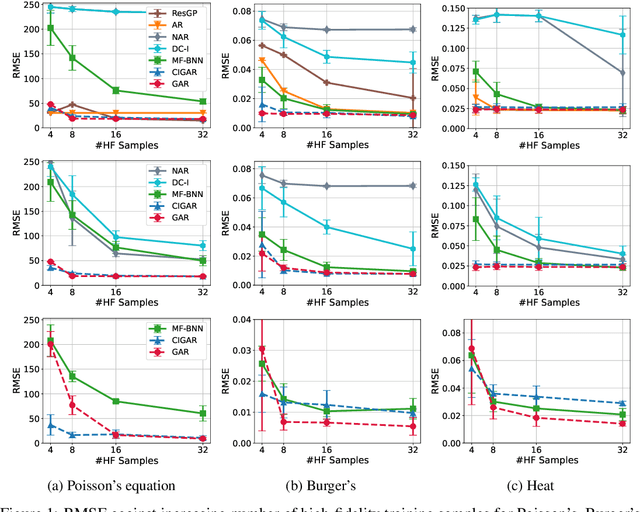
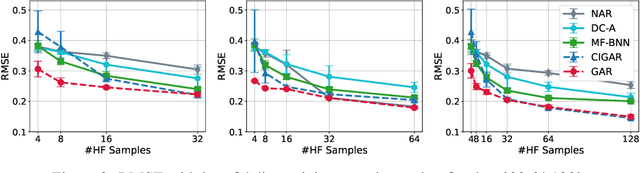
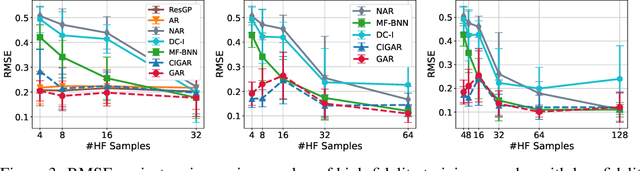
In many scientific research and engineering applications where repeated simulations of complex systems are conducted, a surrogate is commonly adopted to quickly estimate the whole system. To reduce the expensive cost of generating training examples, it has become a promising approach to combine the results of low-fidelity (fast but inaccurate) and high-fidelity (slow but accurate) simulations. Despite the fast developments of multi-fidelity fusion techniques, most existing methods require particular data structures and do not scale well to high-dimensional output. To resolve these issues, we generalize the classic autoregression (AR), which is wildly used due to its simplicity, robustness, accuracy, and tractability, and propose generalized autoregression (GAR) using tensor formulation and latent features. GAR can deal with arbitrary dimensional outputs and arbitrary multifidelity data structure to satisfy the demand of multi-fidelity fusion for complex problems; it admits a fully tractable likelihood and posterior requiring no approximate inference and scales well to high-dimensional problems. Furthermore, we prove the autokrigeability theorem based on GAR in the multi-fidelity case and develop CIGAR, a simplified GAR with the exact predictive mean accuracy with computation reduction by a factor of d 3, where d is the dimensionality of the output. The empirical assessment includes many canonical PDEs and real scientific examples and demonstrates that the proposed method consistently outperforms the SOTA methods with a large margin (up to 6x improvement in RMSE) with only a couple high-fidelity training samples.

High-Dimensional Yield Estimation using Shrinkage Deep Features and Maximization of Integral Entropy Reduction

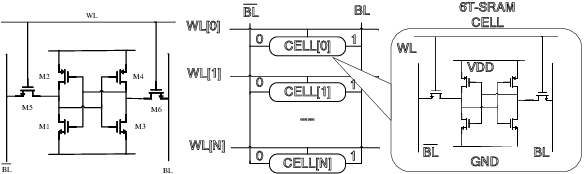
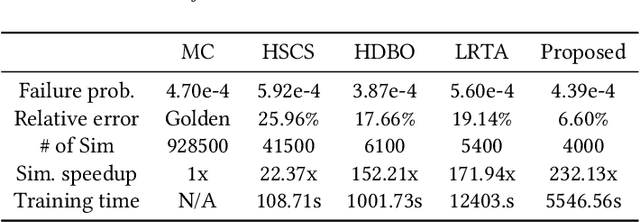
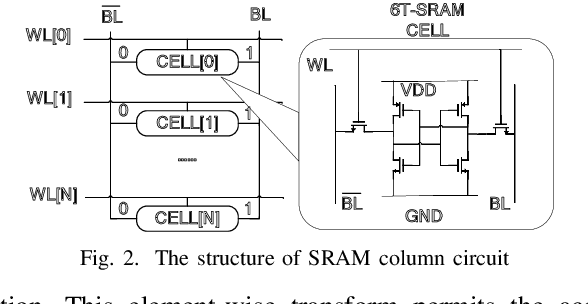
Despite the fast advances in high-sigma yield analysis with the help of machine learning techniques in the past decade, one of the main challenges, the curse of dimensionality, which is inevitable when dealing with modern large-scale circuits, remains unsolved. To resolve this challenge, we propose an absolute shrinkage deep kernel learning, ASDK, which automatically identifies the dominant process variation parameters in a nonlinear-correlated deep kernel and acts as a surrogate model to emulate the expensive SPICE simulation. To further improve the yield estimation efficiency, we propose a novel maximization of approximated entropy reduction for an efficient model update, which is also enhanced with parallel batch sampling for parallel computing, making it ready for practical deployment. Experiments on SRAM column circuits demonstrate the superiority of ASDK over the state-of-the-art (SOTA) approaches in terms of accuracy and efficiency with up to 10.3x speedup over SOTA methods.

Battery Degradation Long-term Forecast Using Gaussian Process Dynamical Models and Knowledge Transfer

Batteries plays an essential role in modern energy ecosystem and are widely used in daily applications such as cell phones and electric vehicles. For many applications, the health status of batteries plays a critical role in the performance of the system by indicating efficient maintenance and on-time replacement. Directly modeling an individual battery using a computational models based on physical rules can be of low-efficiency, in terms of the difficulties in build such a model and the computational effort of tuning and running it especially on the edge. With the rapid development of sensor technology (to provide more insights into the system) and machine learning (to build capable yet fast model), it is now possible to directly build a data-riven model of the battery health status using the data collected from historical battery data (being possibly local and remote) to predict local battery health status in the future accurately. Nevertheless, most data-driven methods are trained based on the local battery data and lack the ability to extract common properties, such as generations and degradation, in the life span of other remote batteries. In this paper, we utilize a Gaussian process dynamical model (GPDM) to build a data-driven model of battery health status and propose a knowledge transfer method to extract common properties in the life span of all batteries to accurately predict the battery health status with and without features extracted from the local battery. For modern benchmark problems, the proposed method outperform the state-of-the-art methods with significant margins in terms of accuracy and is able to accuracy predict the regeneration process.

BoA-PTA, A Bayesian Optimization Accelerated Error-Free SPICE Solver

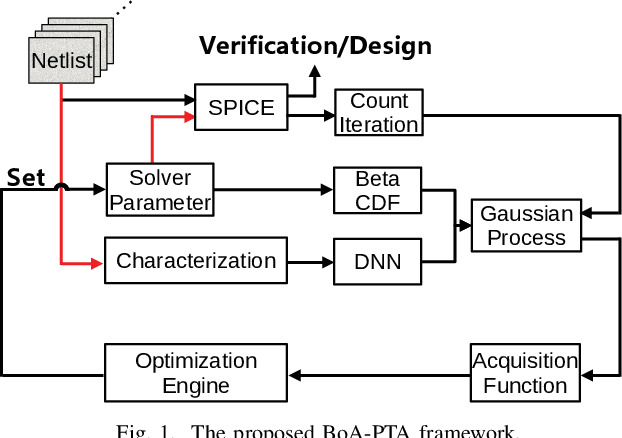
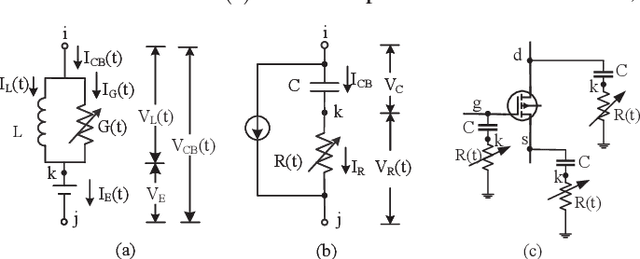
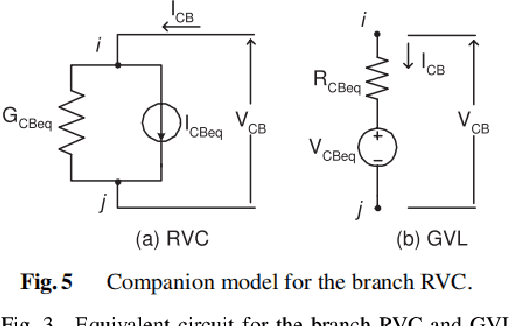
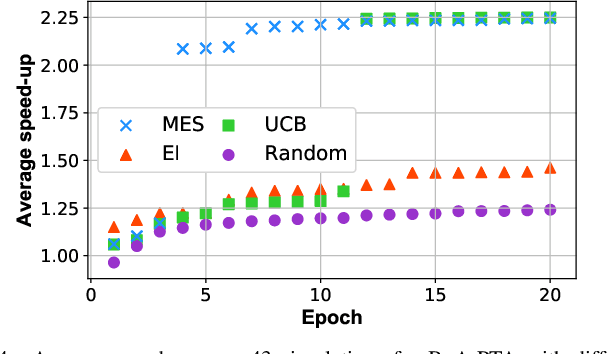
One of the greatest challenges in IC design is the repeated executions of computationally expensive SPICE simulations, particularly when highly complex chip testing/verification is involved. Recently, pseudo transient analysis (PTA) has shown to be one of the most promising continuation SPICE solver. However, the PTA efficiency is highly influenced by the inserted pseudo-parameters. In this work, we proposed BoA-PTA, a Bayesian optimization accelerated PTA that can substantially accelerate simulations and improve convergence performance without introducing extra errors. Furthermore, our method does not require any pre-computation data or offline training. The acceleration framework can either be implemented to speed up ongoing repeated simulations immediately or to improve new simulations of completely different circuits. BoA-PTA is equipped with cutting-edge machine learning techniques, e.g., deep learning, Gaussian process, Bayesian optimization, non-stationary monotonic transformation, and variational inference via parameterization. We assess BoA-PTA in 43 benchmark circuits against other SOTA SPICE solvers and demonstrate an average 2.3x (maximum 3.5x) speed-up over the original CEPTA.

Residual Gaussian Process: A Tractable Nonparametric Bayesian Emulator for Multi-fidelity Simulations

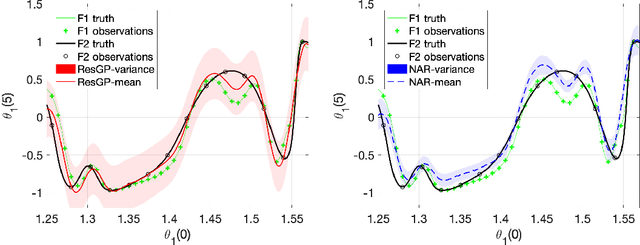
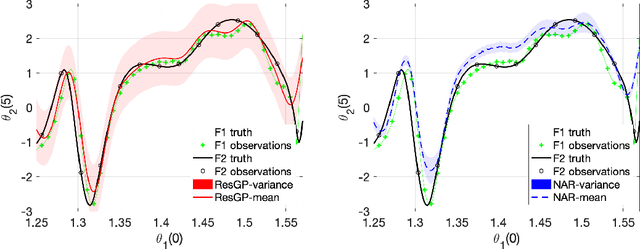
Challenges in multi-fidelity modeling relate to accuracy, uncertainty estimation and high-dimensionality. A novel additive structure is introduced in which the highest fidelity solution is written as a sum of the lowest fidelity solution and residuals between the solutions at successive fidelity levels, with Gaussian process priors placed over the low fidelity solution and each of the residuals. The resulting model is equipped with a closed-form solution for the predictive posterior, making it applicable to advanced, high-dimensional tasks that require uncertainty estimation. Its advantages are demonstrated on univariate benchmarks and on three challenging multivariate problems. It is shown how active learning can be used to enhance the model, especially with a limited computational budget. Furthermore, error bounds are derived for the mean prediction in the univariate case.