Aditi S. Krishnapriyan
Transformers Discover Molecular Structure Without Graph Priors
Oct 02, 2025



Abstract:Graph Neural Networks (GNNs) are the dominant architecture for molecular machine learning, particularly for molecular property prediction and machine learning interatomic potentials (MLIPs). GNNs perform message passing on predefined graphs often induced by a fixed radius cutoff or k-nearest neighbor scheme. While this design aligns with the locality present in many molecular tasks, a hard-coded graph can limit expressivity due to the fixed receptive field and slows down inference with sparse graph operations. In this work, we investigate whether pure, unmodified Transformers trained directly on Cartesian coordinates$\unicode{x2013}$without predefined graphs or physical priors$\unicode{x2013}$can approximate molecular energies and forces. As a starting point for our analysis, we demonstrate how to train a Transformer to competitive energy and force mean absolute errors under a matched training compute budget, relative to a state-of-the-art equivariant GNN on the OMol25 dataset. We discover that the Transformer learns physically consistent patterns$\unicode{x2013}$such as attention weights that decay inversely with interatomic distance$\unicode{x2013}$and flexibly adapts them across different molecular environments due to the absence of hard-coded biases. The use of a standard Transformer also unlocks predictable improvements with respect to scaling training resources, consistent with empirical scaling laws observed in other domains. Our results demonstrate that many favorable properties of GNNs can emerge adaptively in Transformers, challenging the necessity of hard-coded graph inductive biases and pointing toward standardized, scalable architectures for molecular modeling.
Action-Minimization Meets Generative Modeling: Efficient Transition Path Sampling with the Onsager-Machlup Functional
May 01, 2025Abstract:Transition path sampling (TPS), which involves finding probable paths connecting two points on an energy landscape, remains a challenge due to the complexity of real-world atomistic systems. Current machine learning approaches use expensive, task-specific, and data-free training procedures, limiting their ability to benefit from recent advances in atomistic machine learning, such as high-quality datasets and large-scale pre-trained models. In this work, we address TPS by interpreting candidate paths as trajectories sampled from stochastic dynamics induced by the learned score function of pre-trained generative models, specifically denoising diffusion and flow matching. Under these dynamics, finding high-likelihood transition paths becomes equivalent to minimizing the Onsager-Machlup (OM) action functional. This enables us to repurpose pre-trained generative models for TPS in a zero-shot manner, in contrast with bespoke, task-specific TPS models trained in previous work. We demonstrate our approach on varied molecular systems, obtaining diverse, physically realistic transition pathways and generalizing beyond the pre-trained model's original training dataset. Our method can be easily incorporated into new generative models, making it practically relevant as models continue to scale and improve with increased data availability.
Understanding and Mitigating Distribution Shifts For Machine Learning Force Fields
Mar 11, 2025Abstract:Machine Learning Force Fields (MLFFs) are a promising alternative to expensive ab initio quantum mechanical molecular simulations. Given the diversity of chemical spaces that are of interest and the cost of generating new data, it is important to understand how MLFFs generalize beyond their training distributions. In order to characterize and better understand distribution shifts in MLFFs, we conduct diagnostic experiments on chemical datasets, revealing common shifts that pose significant challenges, even for large foundation models trained on extensive data. Based on these observations, we hypothesize that current supervised training methods inadequately regularize MLFFs, resulting in overfitting and learning poor representations of out-of-distribution systems. We then propose two new methods as initial steps for mitigating distribution shifts for MLFFs. Our methods focus on test-time refinement strategies that incur minimal computational cost and do not use expensive ab initio reference labels. The first strategy, based on spectral graph theory, modifies the edges of test graphs to align with graph structures seen during training. Our second strategy improves representations for out-of-distribution systems at test-time by taking gradient steps using an auxiliary objective, such as a cheap physical prior. Our test-time refinement strategies significantly reduce errors on out-of-distribution systems, suggesting that MLFFs are capable of and can move towards modeling diverse chemical spaces, but are not being effectively trained to do so. Our experiments establish clear benchmarks for evaluating the generalization capabilities of the next generation of MLFFs. Our code is available at https://tkreiman.github.io/projects/mlff_distribution_shifts/.
Deep Speech Synthesis from Multimodal Articulatory Representations
Dec 17, 2024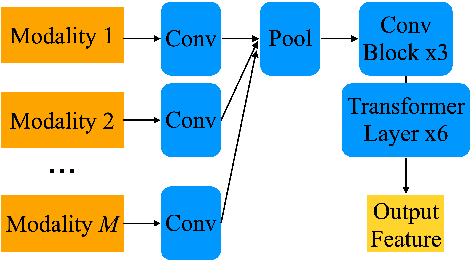
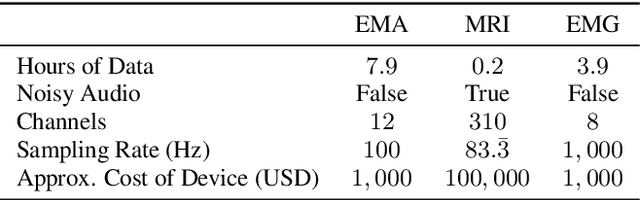
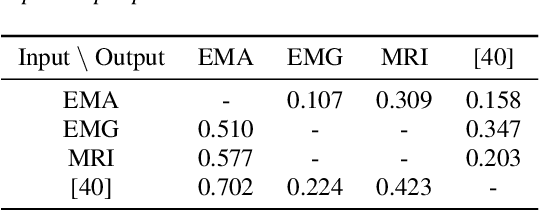

Abstract:The amount of articulatory data available for training deep learning models is much less compared to acoustic speech data. In order to improve articulatory-to-acoustic synthesis performance in these low-resource settings, we propose a multimodal pre-training framework. On single-speaker speech synthesis tasks from real-time magnetic resonance imaging and surface electromyography inputs, the intelligibility of synthesized outputs improves noticeably. For example, compared to prior work, utilizing our proposed transfer learning methods improves the MRI-to-speech performance by 36% word error rate. In addition to these intelligibility results, our multimodal pre-trained models consistently outperform unimodal baselines on three objective and subjective synthesis quality metrics.
The Importance of Being Scalable: Improving the Speed and Accuracy of Neural Network Interatomic Potentials Across Chemical Domains
Oct 31, 2024Abstract:Scaling has been critical in improving model performance and generalization in machine learning. It involves how a model's performance changes with increases in model size or input data, as well as how efficiently computational resources are utilized to support this growth. Despite successes in other areas, the study of scaling in Neural Network Interatomic Potentials (NNIPs) remains limited. NNIPs act as surrogate models for ab initio quantum mechanical calculations. The dominant paradigm here is to incorporate many physical domain constraints into the model, such as rotational equivariance. We contend that these complex constraints inhibit the scaling ability of NNIPs, and are likely to lead to performance plateaus in the long run. In this work, we take an alternative approach and start by systematically studying NNIP scaling strategies. Our findings indicate that scaling the model through attention mechanisms is efficient and improves model expressivity. These insights motivate us to develop an NNIP architecture designed for scalability: the Efficiently Scaled Attention Interatomic Potential (EScAIP). EScAIP leverages a multi-head self-attention formulation within graph neural networks, applying attention at the neighbor-level representations. Implemented with highly-optimized attention GPU kernels, EScAIP achieves substantial gains in efficiency--at least 10x faster inference, 5x less memory usage--compared to existing NNIPs. EScAIP also achieves state-of-the-art performance on a wide range of datasets including catalysts (OC20 and OC22), molecules (SPICE), and materials (MPTrj). We emphasize that our approach should be thought of as a philosophy rather than a specific model, representing a proof-of-concept for developing general-purpose NNIPs that achieve better expressivity through scaling, and continue to scale efficiently with increased computational resources and training data.
General Binding Affinity Guidance for Diffusion Models in Structure-Based Drug Design
Jun 24, 2024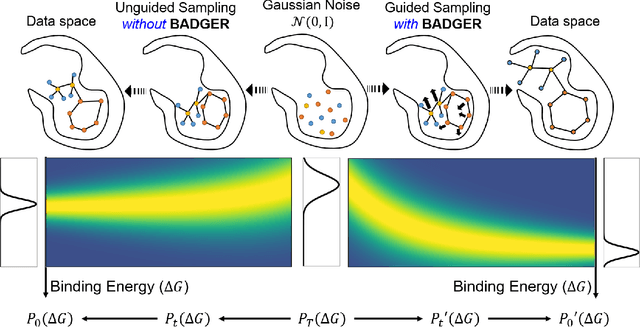
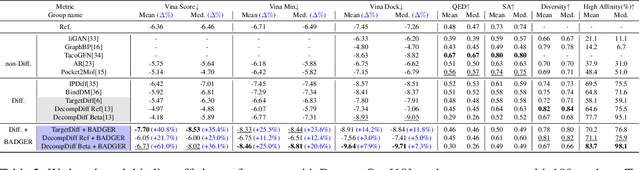

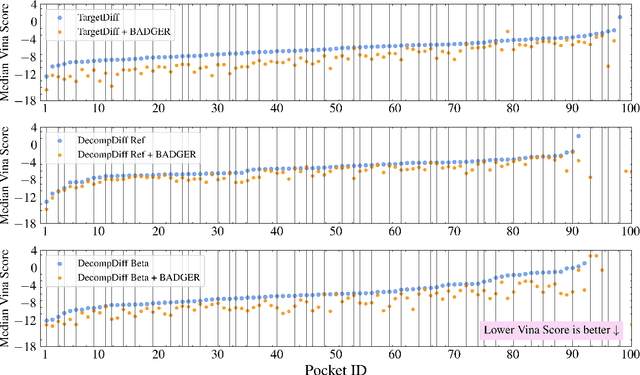
Abstract:Structure-Based Drug Design (SBDD) focuses on generating valid ligands that strongly and specifically bind to a designated protein pocket. Several methods use machine learning for SBDD to generate these ligands in 3D space, conditioned on the structure of a desired protein pocket. Recently, diffusion models have shown success here by modeling the underlying distributions of atomic positions and types. While these methods are effective in considering the structural details of the protein pocket, they often fail to explicitly consider the binding affinity. Binding affinity characterizes how tightly the ligand binds to the protein pocket, and is measured by the change in free energy associated with the binding process. It is one of the most crucial metrics for benchmarking the effectiveness of the interaction between a ligand and protein pocket. To address this, we propose BADGER: Binding Affinity Diffusion Guidance with Enhanced Refinement. BADGER is a general guidance method to steer the diffusion sampling process towards improved protein-ligand binding, allowing us to adjust the distribution of the binding affinity between ligands and proteins. Our method is enabled by using a neural network (NN) to model the energy function, which is commonly approximated by AutoDock Vina (ADV). ADV's energy function is non-differentiable, and estimates the affinity based on the interactions between a ligand and target protein receptor. By using a NN as a differentiable energy function proxy, we utilize the gradient of our learned energy function as a guidance method on top of any trained diffusion model. We show that our method improves the binding affinity of generated ligands to their protein receptors by up to 60\%, significantly surpassing previous machine learning methods. We also show that our guidance method is flexible and can be easily applied to other diffusion-based SBDD frameworks.
Physics-Informed Heterogeneous Graph Neural Networks for DC Blocker Placement
May 16, 2024



Abstract:The threat of geomagnetic disturbances (GMDs) to the reliable operation of the bulk energy system has spurred the development of effective strategies for mitigating their impacts. One such approach involves placing transformer neutral blocking devices, which interrupt the path of geomagnetically induced currents (GICs) to limit their impact. The high cost of these devices and the sparsity of transformers that experience high GICs during GMD events, however, calls for a sparse placement strategy that involves high computational cost. To address this challenge, we developed a physics-informed heterogeneous graph neural network (PIHGNN) for solving the graph-based dc-blocker placement problem. Our approach combines a heterogeneous graph neural network (HGNN) with a physics-informed neural network (PINN) to capture the diverse types of nodes and edges in ac/dc networks and incorporates the physical laws of the power grid. We train the PIHGNN model using a surrogate power flow model and validate it using case studies. Results demonstrate that PIHGNN can effectively and efficiently support the deployment of GIC dc-current blockers, ensuring the continued supply of electricity to meet societal demands. Our approach has the potential to contribute to the development of more reliable and resilient power grids capable of withstanding the growing threat that GMDs pose.
Stability-Aware Training of Neural Network Interatomic Potentials with Differentiable Boltzmann Estimators
Feb 21, 2024Abstract:Neural network interatomic potentials (NNIPs) are an attractive alternative to ab-initio methods for molecular dynamics (MD) simulations. However, they can produce unstable simulations which sample unphysical states, limiting their usefulness for modeling phenomena occurring over longer timescales. To address these challenges, we present Stability-Aware Boltzmann Estimator (StABlE) Training, a multi-modal training procedure which combines conventional supervised training from quantum-mechanical energies and forces with reference system observables, to produce stable and accurate NNIPs. StABlE Training iteratively runs MD simulations to seek out unstable regions, and corrects the instabilities via supervision with a reference observable. The training procedure is enabled by the Boltzmann Estimator, which allows efficient computation of gradients required to train neural networks to system observables, and can detect both global and local instabilities. We demonstrate our methodology across organic molecules, tetrapeptides, and condensed phase systems, along with using three modern NNIP architectures. In all three cases, StABlE-trained models achieve significant improvements in simulation stability and recovery of structural and dynamic observables. In some cases, StABlE-trained models outperform conventional models trained on datasets 50 times larger. As a general framework applicable across NNIP architectures and systems, StABlE Training is a powerful tool for training stable and accurate NNIPs, particularly in the absence of large reference datasets.
Enabling Efficient Equivariant Operations in the Fourier Basis via Gaunt Tensor Products
Jan 18, 2024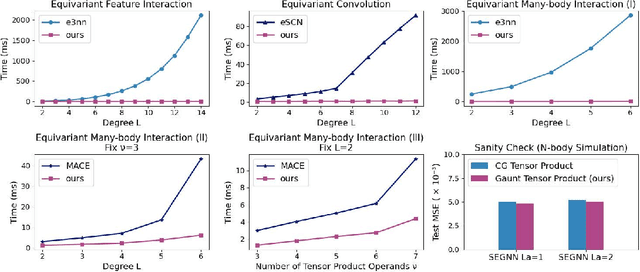
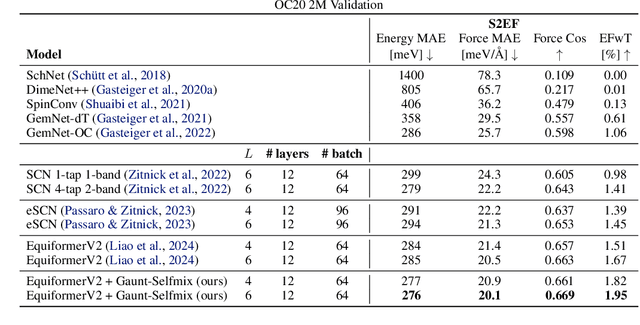
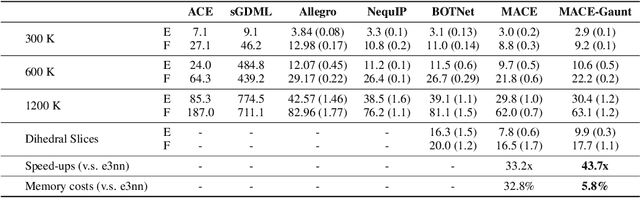
Abstract:Developing equivariant neural networks for the E(3) group plays an important role in modeling 3D data across real-world applications. Enforcing this equivariance primarily involves the tensor products of irreducible representations (irreps). However, the computational complexity of such operations increases significantly as higher-order tensors are used. In this work, we propose a systematic approach to substantially accelerate the computation of the tensor products of irreps. We mathematically connect the commonly used Clebsch-Gordan coefficients to the Gaunt coefficients, which are integrals of products of three spherical harmonics. Through Gaunt coefficients, the tensor product of irreps becomes equivalent to the multiplication between spherical functions represented by spherical harmonics. This perspective further allows us to change the basis for the equivariant operations from spherical harmonics to a 2D Fourier basis. Consequently, the multiplication between spherical functions represented by a 2D Fourier basis can be efficiently computed via the convolution theorem and Fast Fourier Transforms. This transformation reduces the complexity of full tensor products of irreps from $\mathcal{O}(L^6)$ to $\mathcal{O}(L^3)$, where $L$ is the max degree of irreps. Leveraging this approach, we introduce the Gaunt Tensor Product, which serves as a new method to construct efficient equivariant operations across different model architectures. Our experiments on the Open Catalyst Project and 3BPA datasets demonstrate both the increased efficiency and improved performance of our approach.
Investigating the Behavior of Diffusion Models for Accelerating Electronic Structure Calculations
Nov 02, 2023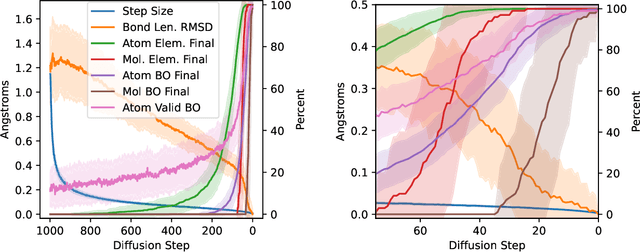
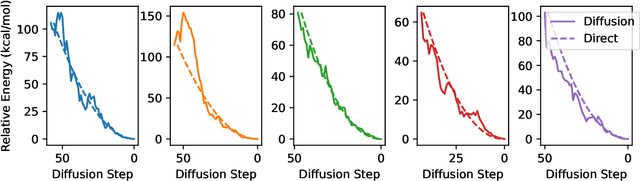
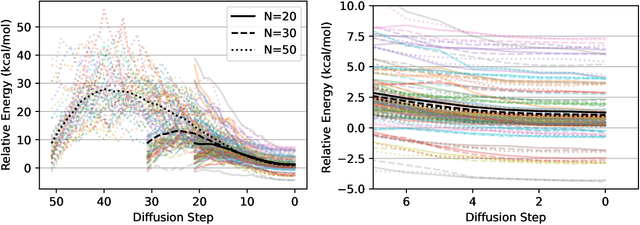
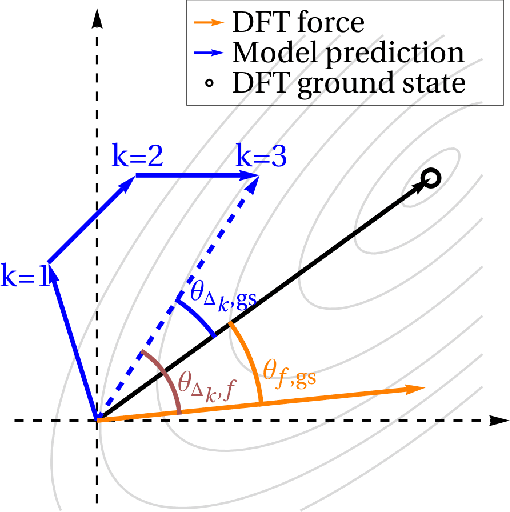
Abstract:We present an investigation into diffusion models for molecular generation, with the aim of better understanding how their predictions compare to the results of physics-based calculations. The investigation into these models is driven by their potential to significantly accelerate electronic structure calculations using machine learning, without requiring expensive first-principles datasets for training interatomic potentials. We find that the inference process of a popular diffusion model for de novo molecular generation is divided into an exploration phase, where the model chooses the atomic species, and a relaxation phase, where it adjusts the atomic coordinates to find a low-energy geometry. As training proceeds, we show that the model initially learns about the first-order structure of the potential energy surface, and then later learns about higher-order structure. We also find that the relaxation phase of the diffusion model can be re-purposed to sample the Boltzmann distribution over conformations and to carry out structure relaxations. For structure relaxations, the model finds geometries with ~10x lower energy than those produced by a classical force field for small organic molecules. Initializing a density functional theory (DFT) relaxation at the diffusion-produced structures yields a >2x speedup to the DFT relaxation when compared to initializing at structures relaxed with a classical force field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge