A General and Streamlined Differentiable Optimization Framework

Differentiating through constrained optimization problems is increasingly central to learning, control, and large-scale decision-making systems, yet practical integration remains challenging due to solver specialization and interface mismatches. This paper presents a general and streamlined framework-an updated DiffOpt.jl-that unifies modeling and differentiation within the Julia optimization stack. The framework computes forward - and reverse-mode solution and objective sensitivities for smooth, potentially nonconvex programs by differentiating the KKT system under standard regularity assumptions. A first-class, JuMP-native parameter-centric API allows users to declare named parameters and obtain derivatives directly with respect to them - even when a parameter appears in multiple constraints and objectives - eliminating brittle bookkeeping from coefficient-level interfaces. We illustrate these capabilities on convex and nonconvex models, including economic dispatch, mean-variance portfolio selection with conic risk constraints, and nonlinear robot inverse kinematics. Two companion studies further demonstrate impact at scale: gradient-based iterative methods for strategic bidding in energy markets and Sobolev-style training of end-to-end optimization proxies using solver-accurate sensitivities. Together, these results demonstrate that differentiable optimization can be deployed as a routine tool for experimentation, learning, calibration, and design-without deviating from standard JuMP modeling practices and while retaining access to a broad ecosystem of solvers.

Nonlinear Optimization with GPU-Accelerated Neural Network Constraints

We propose a reduced-space formulation for optimizing over trained neural networks where the network's outputs and derivatives are evaluated on a GPU. To do this, we treat the neural network as a "gray box" where intermediate variables and constraints are not exposed to the optimization solver. Compared to the full-space formulation, in which intermediate variables and constraints are exposed to the optimization solver, the reduced-space formulation leads to faster solves and fewer iterations in an interior point method. We demonstrate the benefits of this method on two optimization problems: Adversarial generation for a classifier trained on MNIST images and security-constrained optimal power flow with transient feasibility enforced using a neural network surrogate.

Sobolev Training of End-to-End Optimization Proxies

Optimization proxies - machine learning models trained to approximate the solution mapping of parametric optimization problems in a single forward pass - offer dramatic reductions in inference time compared to traditional iterative solvers. This work investigates the integration of solver sensitivities into such end to end proxies via a Sobolev training paradigm and does so in two distinct settings: (i) fully supervised proxies, where exact solver outputs and sensitivities are available, and (ii) self supervised proxies that rely only on the objective and constraint structure of the underlying optimization problem. By augmenting the standard training loss with directional derivative information extracted from the solver, the proxy aligns both its predicted solutions and local derivatives with those of the optimizer. Under Lipschitz continuity assumptions on the true solution mapping, matching first order sensitivities is shown to yield uniform approximation error proportional to the training set covering radius. Empirically, different impacts are observed in each studied setting. On three large Alternating Current Optimal Power Flow benchmarks, supervised Sobolev training cuts mean squared error by up to 56 percent and the median worst case constraint violation by up to 400 percent while keeping the optimality gap below 0.22 percent. For a mean variance portfolio task trained without labeled solutions, self supervised Sobolev training halves the average optimality gap in the medium risk region (standard deviation above 10 percent of budget) and matches the baseline elsewhere. Together, these results highlight Sobolev training whether supervised or self supervised as a path to fast reliable surrogates for safety critical large scale optimization workloads.

Formulations and scalability of neural network surrogates in nonlinear optimization problems

We compare full-space, reduced-space, and gray-box formulations for representing trained neural networks in nonlinear constrained optimization problems. We test these formulations on a transient stability-constrained, security-constrained alternating current optimal power flow (SCOPF) problem where the transient stability criteria are represented by a trained neural network surrogate. Optimization problems are implemented in JuMP and trained neural networks are embedded using a new Julia package: MathOptAI.jl. To study the bottlenecks of the three formulations, we use neural networks with up to 590 million trained parameters. The full-space formulation is bottlenecked by the linear solver used by the optimization algorithm, while the reduced-space formulation is bottlenecked by the algebraic modeling environment and derivative computations. The gray-box formulation is the most scalable and is capable of solving with the largest neural networks tested. It is bottlenecked by evaluation of the neural network's outputs and their derivatives, which may be accelerated with a graphics processing unit (GPU). Leveraging the gray-box formulation and GPU acceleration, we solve our test problem with our largest neural network surrogate in 2.5$\times$ the time required for a simpler SCOPF problem without the stability constraint.

LEVIS: Large Exact Verifiable Input Spaces for Neural Networks

The robustness of neural networks is paramount in safety-critical applications. While most current robustness verification methods assess the worst-case output under the assumption that the input space is known, identifying a verifiable input space $\mathcal{C}$, where no adversarial examples exist, is crucial for effective model selection, robustness evaluation, and the development of reliable control strategies. To address this challenge, we introduce a novel framework, $\texttt{LEVIS}$, comprising $\texttt{LEVIS}$-$\alpha$ and $\texttt{LEVIS}$-$\beta$. $\texttt{LEVIS}$-$\alpha$ locates the largest possible verifiable ball within the central region of $\mathcal{C}$ that intersects at least two boundaries. In contrast, $\texttt{LEVIS}$-$\beta$ integrates multiple verifiable balls to encapsulate the entirety of the verifiable space comprehensively. Our contributions are threefold: (1) We propose $\texttt{LEVIS}$ equipped with three pioneering techniques that identify the maximum verifiable ball and the nearest adversarial point along collinear or orthogonal directions. (2) We offer a theoretical analysis elucidating the properties of the verifiable balls acquired through $\texttt{LEVIS}$-$\alpha$ and $\texttt{LEVIS}$-$\beta$. (3) We validate our methodology across diverse applications, including electrical power flow regression and image classification, showcasing performance enhancements and visualizations of the searching characteristics.

Physics-Informed Heterogeneous Graph Neural Networks for DC Blocker Placement

The threat of geomagnetic disturbances (GMDs) to the reliable operation of the bulk energy system has spurred the development of effective strategies for mitigating their impacts. One such approach involves placing transformer neutral blocking devices, which interrupt the path of geomagnetically induced currents (GICs) to limit their impact. The high cost of these devices and the sparsity of transformers that experience high GICs during GMD events, however, calls for a sparse placement strategy that involves high computational cost. To address this challenge, we developed a physics-informed heterogeneous graph neural network (PIHGNN) for solving the graph-based dc-blocker placement problem. Our approach combines a heterogeneous graph neural network (HGNN) with a physics-informed neural network (PINN) to capture the diverse types of nodes and edges in ac/dc networks and incorporates the physical laws of the power grid. We train the PIHGNN model using a surrogate power flow model and validate it using case studies. Results demonstrate that PIHGNN can effectively and efficiently support the deployment of GIC dc-current blockers, ensuring the continued supply of electricity to meet societal demands. Our approach has the potential to contribute to the development of more reliable and resilient power grids capable of withstanding the growing threat that GMDs pose.

Globally Optimal Boresight Alignment of UAV-LiDAR Systems

In airborne light detection and ranging (LiDAR) systems, misalignments between the LiDAR-scanner and the inertial navigation system (INS) mounted on an unmanned aerial vehicle (UAV)'s frame can lead to inaccurate 3D point clouds. Determining the orientation offset, or boresight error is key to many LiDAR-based applications. In this work, we introduce a mixed-integer quadratically constrained quadratic program (MIQCQP) that can globally solve this misalignment problem. We also propose a nested spatial branch and bound (nsBB) algorithm that improves computational performance. The nsBB relies on novel preprocessing steps that progressively reduce the problem size. In addition, an adaptive grid search (aGS) allowing us to obtain quick heuristic solutions is presented. Our algorithms are open-source, multi-threaded and multi-machine compatible.

Ising Processing Units: Potential and Challenges for Discrete Optimization

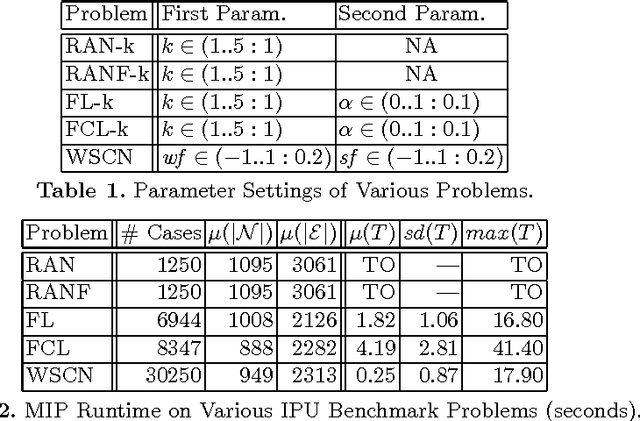
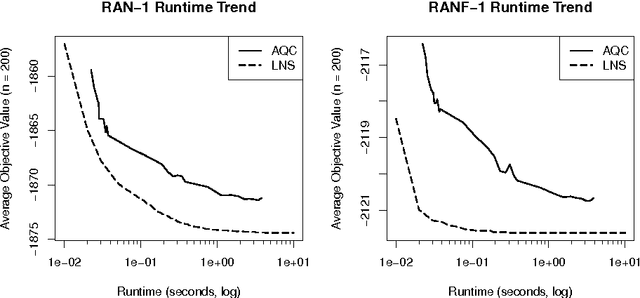
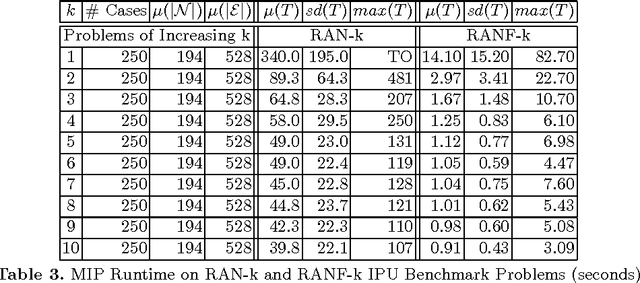
The recent emergence of novel computational devices, such as adiabatic quantum computers, CMOS annealers, and optical parametric oscillators, presents new opportunities for hybrid-optimization algorithms that leverage these kinds of specialized hardware. In this work, we propose the idea of an Ising processing unit as a computational abstraction for these emerging tools. Challenges involved in using and benchmarking these devices are presented, and open-source software tools are proposed to address some of these challenges. The proposed benchmarking tools and methodology are demonstrated by conducting a baseline study of established solution methods to a D-Wave 2X adiabatic quantum computer, one example of a commercially available Ising processing unit.