LEVIS: Large Exact Verifiable Input Spaces for Neural Networks

The robustness of neural networks is paramount in safety-critical applications. While most current robustness verification methods assess the worst-case output under the assumption that the input space is known, identifying a verifiable input space $\mathcal{C}$, where no adversarial examples exist, is crucial for effective model selection, robustness evaluation, and the development of reliable control strategies. To address this challenge, we introduce a novel framework, $\texttt{LEVIS}$, comprising $\texttt{LEVIS}$-$\alpha$ and $\texttt{LEVIS}$-$\beta$. $\texttt{LEVIS}$-$\alpha$ locates the largest possible verifiable ball within the central region of $\mathcal{C}$ that intersects at least two boundaries. In contrast, $\texttt{LEVIS}$-$\beta$ integrates multiple verifiable balls to encapsulate the entirety of the verifiable space comprehensively. Our contributions are threefold: (1) We propose $\texttt{LEVIS}$ equipped with three pioneering techniques that identify the maximum verifiable ball and the nearest adversarial point along collinear or orthogonal directions. (2) We offer a theoretical analysis elucidating the properties of the verifiable balls acquired through $\texttt{LEVIS}$-$\alpha$ and $\texttt{LEVIS}$-$\beta$. (3) We validate our methodology across diverse applications, including electrical power flow regression and image classification, showcasing performance enhancements and visualizations of the searching characteristics.

CAT: Caution Aware Transfer in Reinforcement Learning via Distributional Risk

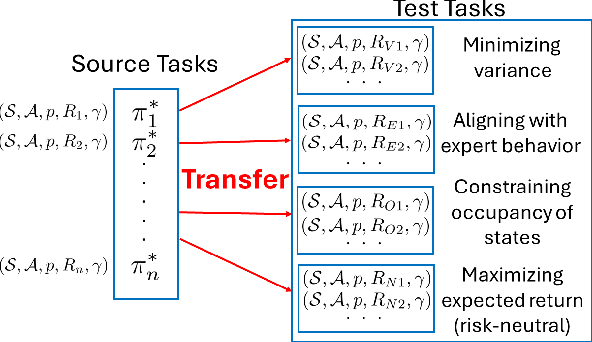
Transfer learning in reinforcement learning (RL) has become a pivotal strategy for improving data efficiency in new, unseen tasks by utilizing knowledge from previously learned tasks. This approach is especially beneficial in real-world deployment scenarios where computational resources are constrained and agents must adapt rapidly to novel environments. However, current state-of-the-art methods often fall short in ensuring safety during the transfer process, particularly when unforeseen risks emerge in the deployment phase. In this work, we address these limitations by introducing a novel Caution-Aware Transfer Learning (CAT) framework. Unlike traditional approaches that limit risk considerations to mean-variance, we define "caution" as a more generalized and comprehensive notion of risk. Our core innovation lies in optimizing a weighted sum of reward return and caution-based on state-action occupancy measures-during the transfer process, allowing for a rich representation of diverse risk factors. To the best of our knowledge, this is the first work to explore the optimization of such a generalized risk notion within the context of transfer RL. Our contributions are threefold: (1) We propose a Caution-Aware Transfer (CAT) framework that evaluates source policies within the test environment and constructs a new policy that balances reward maximization and caution. (2) We derive theoretical sub-optimality bounds for our method, providing rigorous guarantees of its efficacy. (3) We empirically validate CAT, demonstrating that it consistently outperforms existing methods by delivering safer policies under varying risk conditions in the test tasks.