Physics-Informed Heterogeneous Graph Neural Networks for DC Blocker Placement

The threat of geomagnetic disturbances (GMDs) to the reliable operation of the bulk energy system has spurred the development of effective strategies for mitigating their impacts. One such approach involves placing transformer neutral blocking devices, which interrupt the path of geomagnetically induced currents (GICs) to limit their impact. The high cost of these devices and the sparsity of transformers that experience high GICs during GMD events, however, calls for a sparse placement strategy that involves high computational cost. To address this challenge, we developed a physics-informed heterogeneous graph neural network (PIHGNN) for solving the graph-based dc-blocker placement problem. Our approach combines a heterogeneous graph neural network (HGNN) with a physics-informed neural network (PINN) to capture the diverse types of nodes and edges in ac/dc networks and incorporates the physical laws of the power grid. We train the PIHGNN model using a surrogate power flow model and validate it using case studies. Results demonstrate that PIHGNN can effectively and efficiently support the deployment of GIC dc-current blockers, ensuring the continued supply of electricity to meet societal demands. Our approach has the potential to contribute to the development of more reliable and resilient power grids capable of withstanding the growing threat that GMDs pose.

Deep Learning and Spectral Embedding for Graph Partitioning

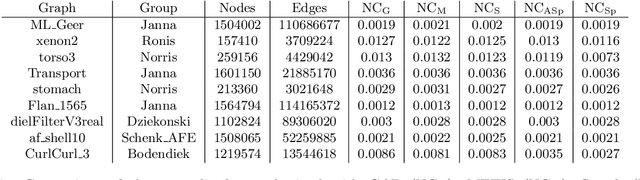
We present a graph bisection and partitioning algorithm based on graph neural networks. For each node in the graph, the network outputs probabilities for each of the partitions. The graph neural network consists of two modules: an embedding phase and a partitioning phase. The embedding phase is trained first by minimizing a loss function inspired by spectral graph theory. The partitioning module is trained through a loss function that corresponds to the expected value of the normalized cut. Both parts of the neural network rely on SAGE convolutional layers and graph coarsening using heavy edge matching. The multilevel structure of the neural network is inspired by the multigrid algorithm. Our approach generalizes very well to bigger graphs and has partition quality comparable to METIS, Scotch and spectral partitioning, with shorter runtime compared to METIS and spectral partitioning.

Graph Partitioning and Sparse Matrix Ordering using Reinforcement Learning

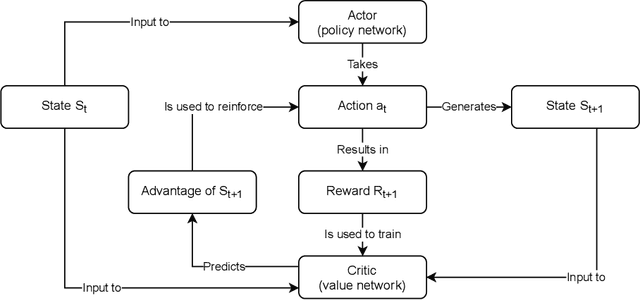
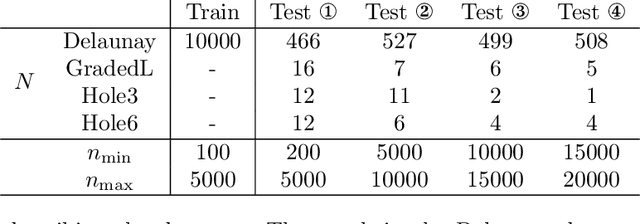
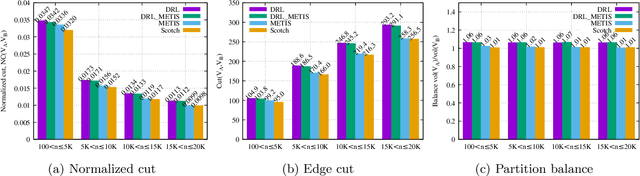
We present a novel method for graph partitioning, based on reinforcement learning and graph convolutional neural networks. The new reinforcement learning based approach is used to refine a given partitioning obtained on a coarser representation of the graph, and the algorithm is applied recursively. The neural network is implemented using graph attention layers, and trained using an advantage actor critic (A2C) agent. We present two variants, one for finding an edge separator that minimizes the normalized cut or quotient cut, and one that finds a small vertex separator. The vertex separators are then used to construct a nested dissection ordering for permuting a sparse matrix so that its triangular factorization will incur less fill-in. The partitioning quality is compared with partitions obtained using METIS and Scotch, and the nested dissection ordering is evaluated in the sparse solver SuperLU. Our results show that the proposed method achieves similar partitioning quality than METIS and Scotch. Furthermore, the method generalizes from one class of graphs to another, and works well on a variety of graphs from the SuiteSparse sparse matrix collection.

A Study of Clustering Techniques and Hierarchical Matrix Formats for Kernel Ridge Regression

We present memory-efficient and scalable algorithms for kernel methods used in machine learning. Using hierarchical matrix approximations for the kernel matrix the memory requirements, the number of floating point operations, and the execution time are drastically reduced compared to standard dense linear algebra routines. We consider both the general $\mathcal{H}$ matrix hierarchical format as well as Hierarchically Semi-Separable (HSS) matrices. Furthermore, we investigate the impact of several preprocessing and clustering techniques on the hierarchical matrix compression. Effective clustering of the input leads to a ten-fold increase in efficiency of the compression. The algorithms are implemented using the STRUMPACK solver library. These results confirm that --- with correct tuning of the hyperparameters --- classification using kernel ridge regression with the compressed matrix does not lose prediction accuracy compared to the exact --- not compressed --- kernel matrix and that our approach can be extended to $\mathcal{O}(1M)$ datasets, for which computation with the full kernel matrix becomes prohibitively expensive. We present numerical experiments in a distributed memory environment up to 1,024 processors of the NERSC's Cori supercomputer using well-known datasets to the machine learning community that range from dimension 8 up to 784.