A Cosmic-Scale Benchmark for Symmetry-Preserving Data Processing

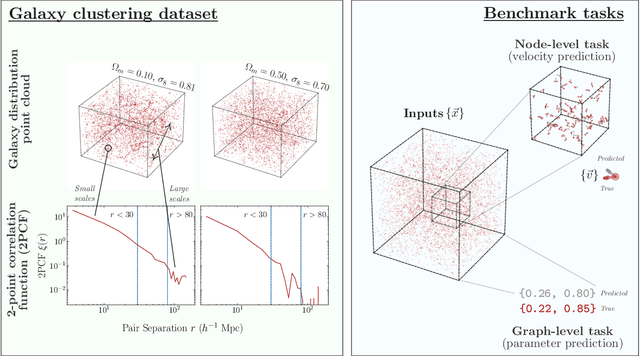
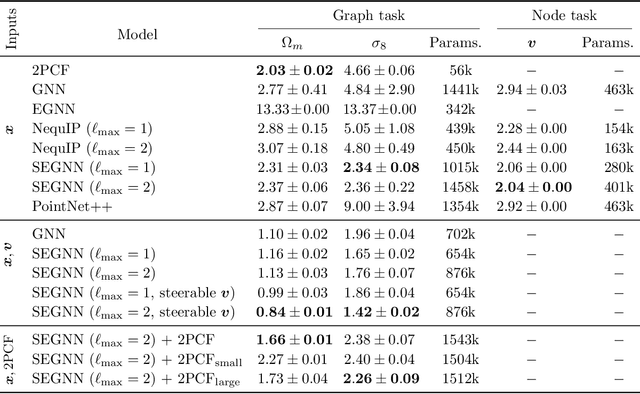
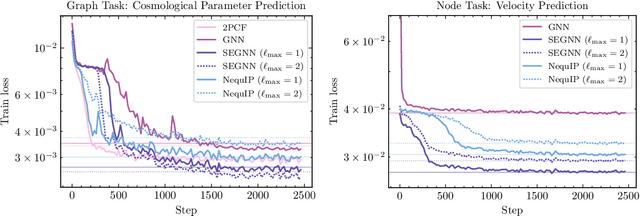
Efficiently processing structured point cloud data while preserving multiscale information is a key challenge across domains, from graphics to atomistic modeling. Using a curated dataset of simulated galaxy positions and properties, represented as point clouds, we benchmark the ability of graph neural networks to simultaneously capture local clustering environments and long-range correlations. Given the homogeneous and isotropic nature of the Universe, the data exhibits a high degree of symmetry. We therefore focus on evaluating the performance of Euclidean symmetry-preserving ($E(3)$-equivariant) graph neural networks, showing that they can outperform non-equivariant counterparts and domain-specific information extraction techniques in downstream performance as well as simulation-efficiency. However, we find that current architectures fail to capture information from long-range correlations as effectively as domain-specific baselines, motivating future work on architectures better suited for extracting long-range information.

EquiJump: Protein Dynamics Simulation via SO(3)-Equivariant Stochastic Interpolants

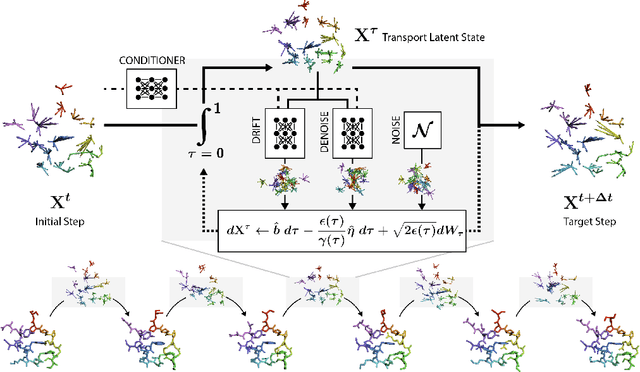
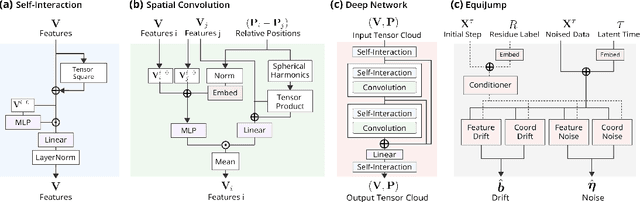
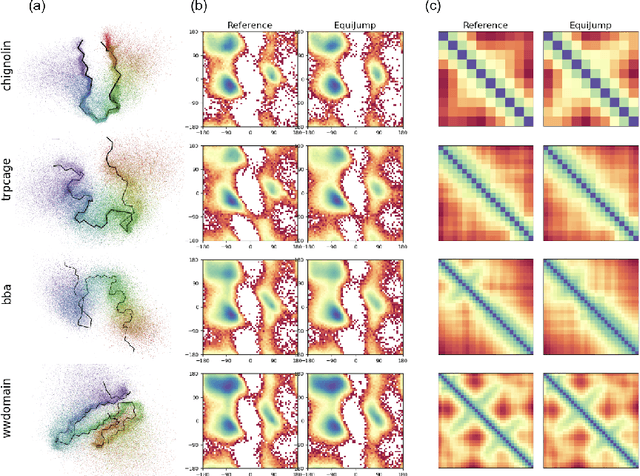
Mapping the conformational dynamics of proteins is crucial for elucidating their functional mechanisms. While Molecular Dynamics (MD) simulation enables detailed time evolution of protein motion, its computational toll hinders its use in practice. To address this challenge, multiple deep learning models for reproducing and accelerating MD have been proposed drawing on transport-based generative methods. However, existing work focuses on generation through transport of samples from prior distributions, that can often be distant from the data manifold. The recently proposed framework of stochastic interpolants, instead, enables transport between arbitrary distribution endpoints. Building upon this work, we introduce EquiJump, a transferable SO(3)-equivariant model that bridges all-atom protein dynamics simulation time steps directly. Our approach unifies diverse sampling methods and is benchmarked against existing models on trajectory data of fast folding proteins. EquiJump achieves state-of-the-art results on dynamics simulation with a transferable model on all of the fast folding proteins.

Relaxed Equivariant Graph Neural Networks

3D Euclidean symmetry equivariant neural networks have demonstrated notable success in modeling complex physical systems. We introduce a framework for relaxed $E(3)$ graph equivariant neural networks that can learn and represent symmetry breaking within continuous groups. Building on the existing e3nn framework, we propose the use of relaxed weights to allow for controlled symmetry breaking. We show empirically that these relaxed weights learn the correct amount of symmetry breaking.

A Recipe for Charge Density Prediction

In density functional theory, charge density is the core attribute of atomic systems from which all chemical properties can be derived. Machine learning methods are promising in significantly accelerating charge density prediction, yet existing approaches either lack accuracy or scalability. We propose a recipe that can achieve both. In particular, we identify three key ingredients: (1) representing the charge density with atomic and virtual orbitals (spherical fields centered at atom/virtual coordinates); (2) using expressive and learnable orbital basis sets (basis function for the spherical fields); and (3) using high-capacity equivariant neural network architecture. Our method achieves state-of-the-art accuracy while being more than an order of magnitude faster than existing methods. Furthermore, our method enables flexible efficiency-accuracy trade-offs by adjusting the model/basis sizes.

Generalizing Denoising to Non-Equilibrium Structures Improves Equivariant Force Fields

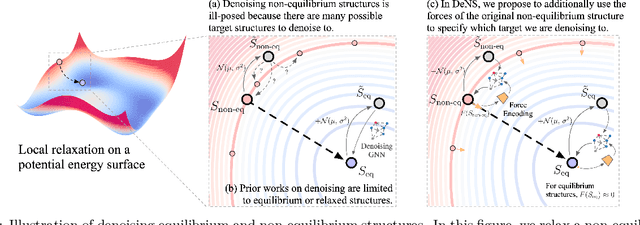
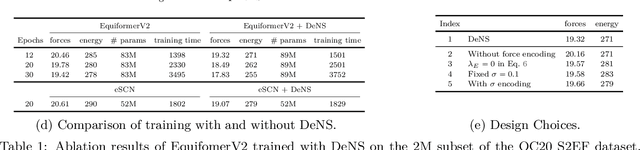
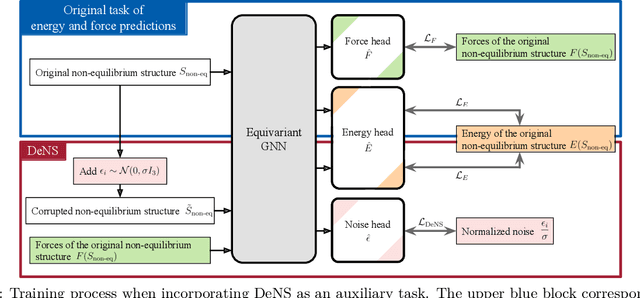
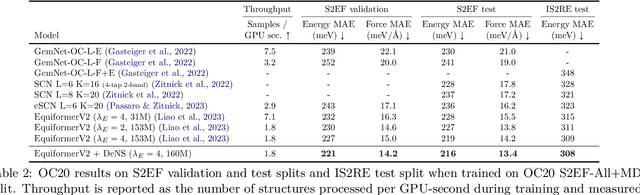
Understanding the interactions of atoms such as forces in 3D atomistic systems is fundamental to many applications like molecular dynamics and catalyst design. However, simulating these interactions requires compute-intensive ab initio calculations and thus results in limited data for training neural networks. In this paper, we propose to use denoising non-equilibrium structures (DeNS) as an auxiliary task to better leverage training data and improve performance. For training with DeNS, we first corrupt a 3D structure by adding noise to its 3D coordinates and then predict the noise. Different from previous works on denoising, which are limited to equilibrium structures, the proposed method generalizes denoising to a much larger set of non-equilibrium structures. The main difference is that a non-equilibrium structure does not correspond to local energy minima and has non-zero forces, and therefore it can have many possible atomic positions compared to an equilibrium structure. This makes denoising non-equilibrium structures an ill-posed problem since the target of denoising is not uniquely defined. Our key insight is to additionally encode the forces of the original non-equilibrium structure to specify which non-equilibrium structure we are denoising. Concretely, given a corrupted non-equilibrium structure and the forces of the original one, we predict the non-equilibrium structure satisfying the input forces instead of any arbitrary structures. Since DeNS requires encoding forces, DeNS favors equivariant networks, which can easily incorporate forces and other higher-order tensors in node embeddings. We study the effectiveness of training equivariant networks with DeNS on OC20, OC22 and MD17 datasets and demonstrate that DeNS can achieve new state-of-the-art results on OC20 and OC22 and significantly improve training efficiency on MD17.

Equivariant Symmetry Breaking Sets

Equivariant neural networks (ENNs) have been shown to be extremely effective in applications involving underlying symmetries. By construction ENNs cannot produce lower symmetry outputs given a higher symmetry input. However, spontaneous symmetry breaking occurs in many physical systems and we may obtain a less symmetric stable state from an initial highly symmetric one. Hence, it is imperative that we understand how to systematically break symmetry in ENNs. In this work, we propose a novel symmetry breaking framework that is fully equivariant. We emphasize that our approach is general and applicable to equivariance under any group. To achieve this, we introduce the idea of symmetry breaking sets (SBS). Rather than redesign existing networks, we design sets of symmetry breaking objects which we feed into our network based on the symmetry of our inputs and outputs. We show there is a natural way to define equivariance on these sets, which gives an additional constraint. Minimizing the size of these sets equates to data efficiency. We prove that minimizing these sets translates to a well studied group theory problem, and tabulate solutions to this problem for the point groups. Finally, we provide some examples of symmetry breaking to demonstrate how our approach works in practice.

Symphony: Symmetry-Equivariant Point-Centered Spherical Harmonics for Molecule Generation

We present Symphony, an $E(3)$-equivariant autoregressive generative model for 3D molecular geometries that iteratively builds a molecule from molecular fragments. Existing autoregressive models such as G-SchNet and G-SphereNet for molecules utilize rotationally invariant features to respect the 3D symmetries of molecules. In contrast, Symphony uses message-passing with higher-degree $E(3)$-equivariant features. This allows a novel representation of probability distributions via spherical harmonic signals to efficiently model the 3D geometry of molecules. We show that Symphony is able to accurately generate small molecules from the QM9 dataset, outperforming existing autoregressive models and approaching the performance of diffusion models.

Ophiuchus: Scalable Modeling of Protein Structures through Hierarchical Coarse-graining SO(3)-Equivariant Autoencoders

Three-dimensional native states of natural proteins display recurring and hierarchical patterns. Yet, traditional graph-based modeling of protein structures is often limited to operate within a single fine-grained resolution, and lacks hourglass neural architectures to learn those high-level building blocks. We narrow this gap by introducing Ophiuchus, an SO(3)-equivariant coarse-graining model that efficiently operates on all heavy atoms of standard protein residues, while respecting their relevant symmetries. Our model departs from current approaches that employ graph modeling, instead focusing on local convolutional coarsening to model sequence-motif interactions in log-linear length complexity. We train Ophiuchus on contiguous fragments of PDB monomers, investigating its reconstruction capabilities across different compression rates. We examine the learned latent space and demonstrate its prompt usage in conformational interpolation, comparing interpolated trajectories to structure snapshots from the PDBFlex dataset. Finally, we leverage denoising diffusion probabilistic models (DDPM) to efficiently sample readily-decodable latent embeddings of diverse miniproteins. Our experiments demonstrate Ophiuchus to be a scalable basis for efficient protein modeling and generation.

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

EquiformerV2: Improved Equivariant Transformer for Scaling to Higher-Degree Representations

Equivariant Transformers such as Equiformer have demonstrated the efficacy of applying Transformers to the domain of 3D atomistic systems. However, they are still limited to small degrees of equivariant representations due to their computational complexity. In this paper, we investigate whether these architectures can scale well to higher degrees. Starting from Equiformer, we first replace $SO(3)$ convolutions with eSCN convolutions to efficiently incorporate higher-degree tensors. Then, to better leverage the power of higher degrees, we propose three architectural improvements -- attention re-normalization, separable $S^2$ activation and separable layer normalization. Putting this all together, we propose EquiformerV2, which outperforms previous state-of-the-art methods on the large-scale OC20 dataset by up to $12\%$ on forces, $4\%$ on energies, offers better speed-accuracy trade-offs, and $2\times$ reduction in DFT calculations needed for computing adsorption energies.