EquiJump: Protein Dynamics Simulation via SO(3)-Equivariant Stochastic Interpolants

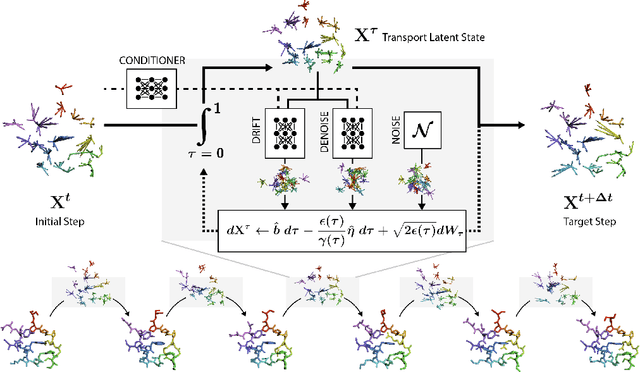
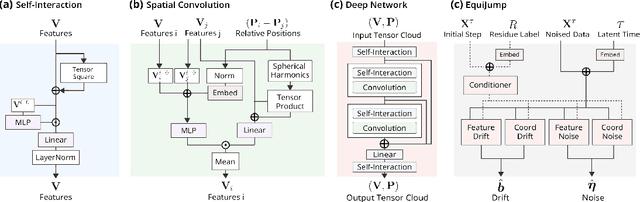
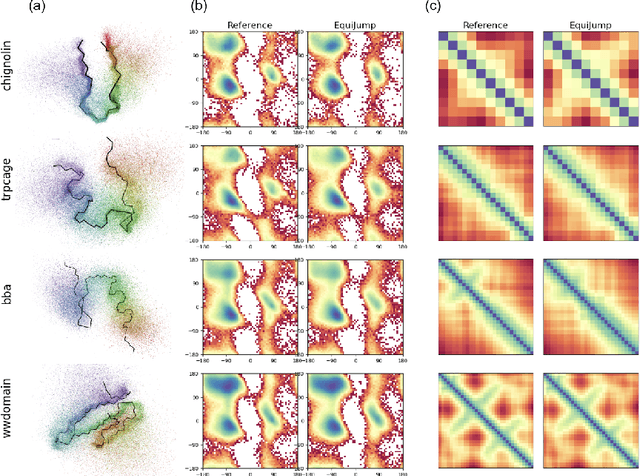
Mapping the conformational dynamics of proteins is crucial for elucidating their functional mechanisms. While Molecular Dynamics (MD) simulation enables detailed time evolution of protein motion, its computational toll hinders its use in practice. To address this challenge, multiple deep learning models for reproducing and accelerating MD have been proposed drawing on transport-based generative methods. However, existing work focuses on generation through transport of samples from prior distributions, that can often be distant from the data manifold. The recently proposed framework of stochastic interpolants, instead, enables transport between arbitrary distribution endpoints. Building upon this work, we introduce EquiJump, a transferable SO(3)-equivariant model that bridges all-atom protein dynamics simulation time steps directly. Our approach unifies diverse sampling methods and is benchmarked against existing models on trajectory data of fast folding proteins. EquiJump achieves state-of-the-art results on dynamics simulation with a transferable model on all of the fast folding proteins.

LATTE: an atomic environment descriptor based on Cartesian tensor contractions

We propose a new descriptor for local atomic environments, to be used in combination with machine learning models for the construction of interatomic potentials. The Local Atomic Tensors Trainable Expansion (LATTE) allows for the efficient construction of a variable number of many-body terms with learnable parameters, resulting in a descriptor that is efficient, expressive, and can be scaled to suit different accuracy and computational cost requirements. We compare this new descriptor to existing ones on several systems, showing it to be competitive with very fast potentials at one end of the spectrum, and extensible to an accuracy close to the state of the art.

PANNA 2.0: Efficient neural network interatomic potentials and new architectures

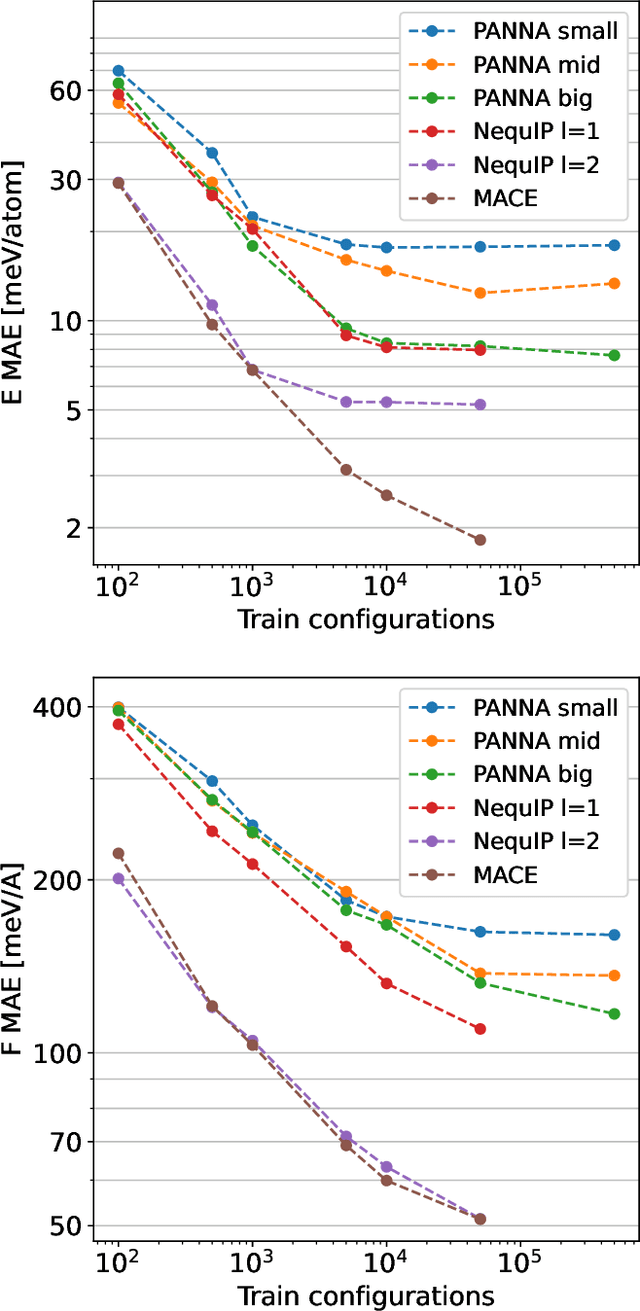
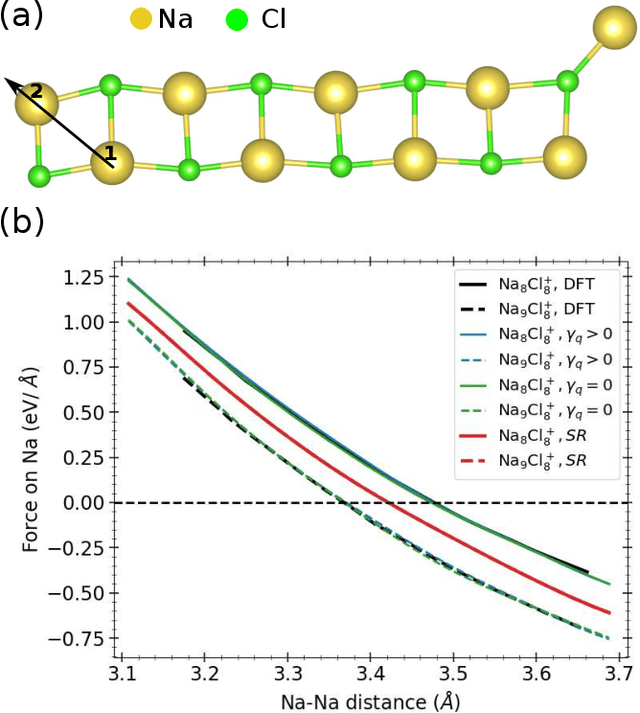
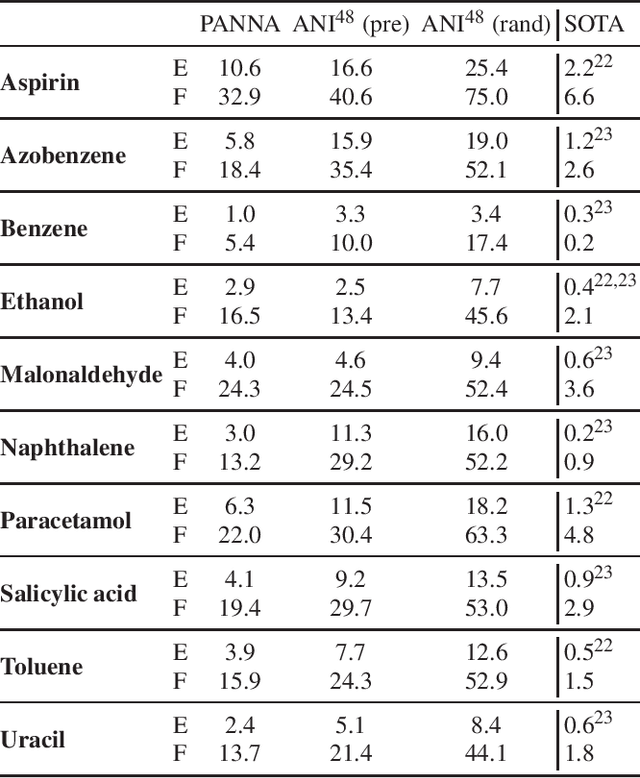
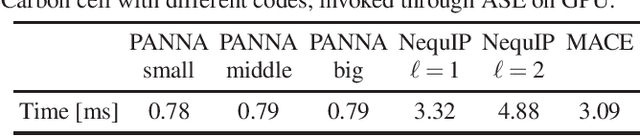
We present the latest release of PANNA 2.0 (Properties from Artificial Neural Network Architectures), a code for the generation of neural network interatomic potentials based on local atomic descriptors and multilayer perceptrons. Built on a new back end, this new release of PANNA features improved tools for customizing and monitoring network training, better GPU support including a fast descriptor calculator, new plugins for external codes and a new architecture for the inclusion of long-range electrostatic interactions through a variational charge equilibration scheme. We present an overview of the main features of the new code, and several benchmarks comparing the accuracy of PANNA models to the state of the art, on commonly used benchmarks as well as richer datasets.

Sifting out the features by pruning: Are convolutional networks the winning lottery ticket of fully connected ones?

Pruning methods can considerably reduce the size of artificial neural networks without harming their performance. In some cases, they can even uncover sub-networks that, when trained in isolation, match or surpass the test accuracy of their dense counterparts. Here we study the inductive bias that pruning imprints in such "winning lottery tickets". Focusing on visual tasks, we analyze the architecture resulting from iterative magnitude pruning of a simple fully connected network (FCN). We show that the surviving node connectivity is local in input space, and organized in patterns reminiscent of the ones found in convolutional networks (CNN). We investigate the role played by data and tasks in shaping the architecture of pruned sub-networks. Our results show that the winning lottery tickets of FCNs display the key features of CNNs. The ability of such automatic network-simplifying procedure to recover the key features "hand-crafted" in the design of CNNs suggests interesting applications to other datasets and tasks, in order to discover new and efficient architectural inductive biases.

An analytic theory of shallow networks dynamics for hinge loss classification

Neural networks have been shown to perform incredibly well in classification tasks over structured high-dimensional datasets. However, the learning dynamics of such networks is still poorly understood. In this paper we study in detail the training dynamics of a simple type of neural network: a single hidden layer trained to perform a classification task. We show that in a suitable mean-field limit this case maps to a single-node learning problem with a time-dependent dataset determined self-consistently from the average nodes population. We specialize our theory to the prototypical case of a linearly separable dataset and a linear hinge loss, for which the dynamics can be explicitly solved. This allow us to address in a simple setting several phenomena appearing in modern networks such as slowing down of training dynamics, crossover between rich and lazy learning, and overfitting. Finally, we asses the limitations of mean-field theory by studying the case of large but finite number of nodes and of training samples.