Optimizing Data Distribution and Kernel Performance for Efficient Training of Chemistry Foundation Models: A Case Study with MACE

Chemistry Foundation Models (CFMs) that leverage Graph Neural Networks (GNNs) operating on 3D molecular graph structures are becoming indispensable tools for computational chemists and materials scientists. These models facilitate the understanding of matter and the discovery of new molecules and materials. In contrast to GNNs operating on a large homogeneous graphs, GNNs used by CFMs process a large number of geometric graphs of varying sizes, requiring different optimization strategies than those developed for large homogeneous GNNs. This paper presents optimizations for two critical phases of CFM training: data distribution and model training, targeting MACE - a state-of-the-art CFM. We address the challenge of load balancing in data distribution by formulating it as a multi-objective bin packing problem. We propose an iterative algorithm that provides a highly effective, fast, and practical solution, ensuring efficient data distribution. For the training phase, we identify symmetric tensor contraction as the key computational kernel in MACE and optimize this kernel to improve the overall performance. Our combined approach of balanced data distribution and kernel optimization significantly enhances the training process of MACE. Experimental results demonstrate a substantial speedup, reducing per-epoch execution time for training from 12 to 2 minutes on 740 GPUs with a 2.6M sample dataset.

Geometry-Informed Neural Operator for Large-Scale 3D PDEs

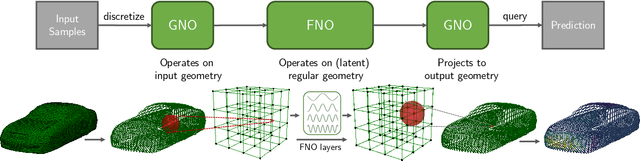
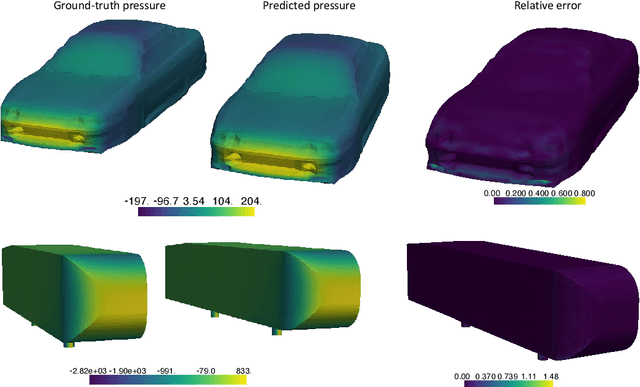
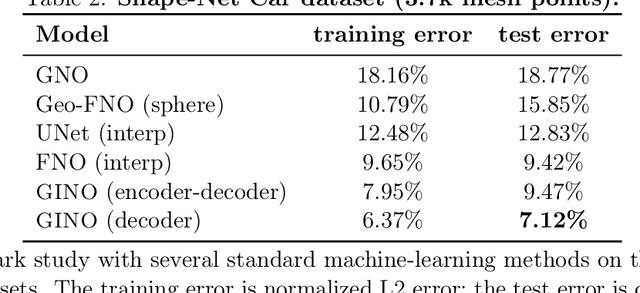
We propose the geometry-informed neural operator (GINO), a highly efficient approach to learning the solution operator of large-scale partial differential equations with varying geometries. GINO uses a signed distance function and point-cloud representations of the input shape and neural operators based on graph and Fourier architectures to learn the solution operator. The graph neural operator handles irregular grids and transforms them into and from regular latent grids on which Fourier neural operator can be efficiently applied. GINO is discretization-convergent, meaning the trained model can be applied to arbitrary discretization of the continuous domain and it converges to the continuum operator as the discretization is refined. To empirically validate the performance of our method on large-scale simulation, we generate the industry-standard aerodynamics dataset of 3D vehicle geometries with Reynolds numbers as high as five million. For this large-scale 3D fluid simulation, numerical methods are expensive to compute surface pressure. We successfully trained GINO to predict the pressure on car surfaces using only five hundred data points. The cost-accuracy experiments show a $26,000 \times$ speed-up compared to optimized GPU-based computational fluid dynamics (CFD) simulators on computing the drag coefficient. When tested on new combinations of geometries and boundary conditions (inlet velocities), GINO obtains a one-fourth reduction in error rate compared to deep neural network approaches.

Graph Posterior Network: Bayesian Predictive Uncertainty for Node Classification

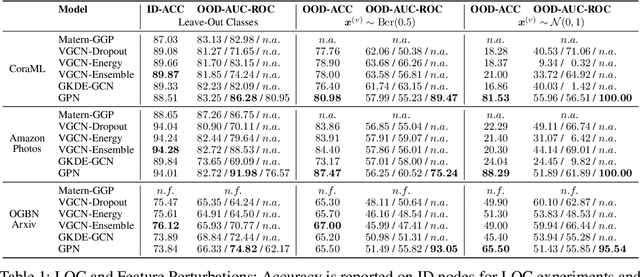
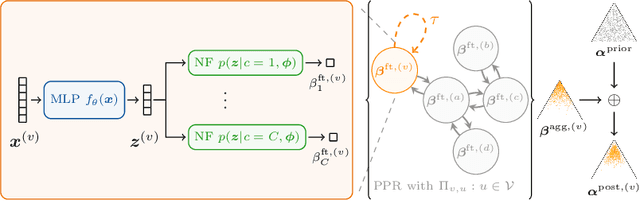
The interdependence between nodes in graphs is key to improve class predictions on nodes and utilized in approaches like Label Propagation (LP) or in Graph Neural Networks (GNN). Nonetheless, uncertainty estimation for non-independent node-level predictions is under-explored. In this work, we explore uncertainty quantification for node classification in three ways: (1) We derive three axioms explicitly characterizing the expected predictive uncertainty behavior in homophilic attributed graphs. (2) We propose a new model Graph Posterior Network (GPN) which explicitly performs Bayesian posterior updates for predictions on interdependent nodes. GPN provably obeys the proposed axioms. (3) We extensively evaluate GPN and a strong set of baselines on semi-supervised node classification including detection of anomalous features, and detection of left-out classes. GPN outperforms existing approaches for uncertainty estimation in the experiments.