Geometry-Informed Neural Operator for Large-Scale 3D PDEs

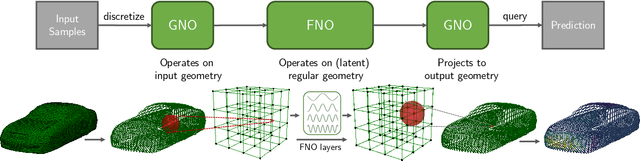
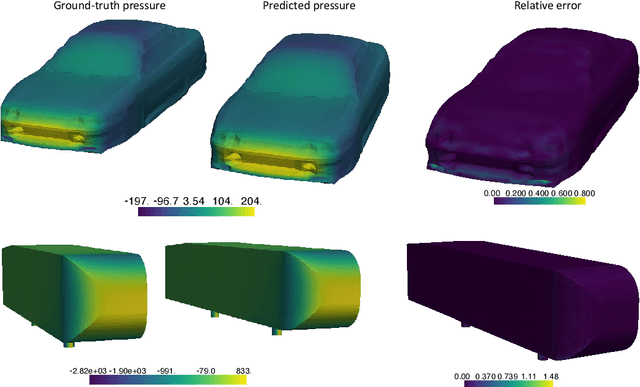
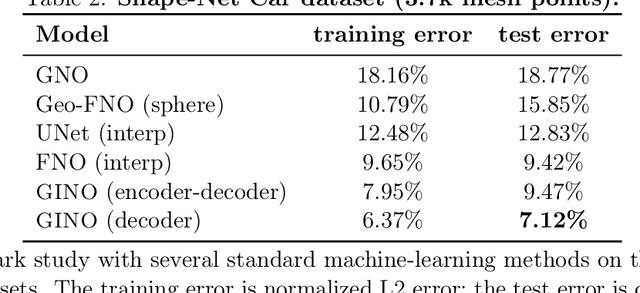
We propose the geometry-informed neural operator (GINO), a highly efficient approach to learning the solution operator of large-scale partial differential equations with varying geometries. GINO uses a signed distance function and point-cloud representations of the input shape and neural operators based on graph and Fourier architectures to learn the solution operator. The graph neural operator handles irregular grids and transforms them into and from regular latent grids on which Fourier neural operator can be efficiently applied. GINO is discretization-convergent, meaning the trained model can be applied to arbitrary discretization of the continuous domain and it converges to the continuum operator as the discretization is refined. To empirically validate the performance of our method on large-scale simulation, we generate the industry-standard aerodynamics dataset of 3D vehicle geometries with Reynolds numbers as high as five million. For this large-scale 3D fluid simulation, numerical methods are expensive to compute surface pressure. We successfully trained GINO to predict the pressure on car surfaces using only five hundred data points. The cost-accuracy experiments show a $26,000 \times$ speed-up compared to optimized GPU-based computational fluid dynamics (CFD) simulators on computing the drag coefficient. When tested on new combinations of geometries and boundary conditions (inlet velocities), GINO obtains a one-fourth reduction in error rate compared to deep neural network approaches.

Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere

Fourier Neural Operators (FNOs) have proven to be an efficient and effective method for resolution-independent operator learning in a broad variety of application areas across scientific machine learning. A key reason for their success is their ability to accurately model long-range dependencies in spatio-temporal data by learning global convolutions in a computationally efficient manner. To this end, FNOs rely on the discrete Fourier transform (DFT), however, DFTs cause visual and spectral artifacts as well as pronounced dissipation when learning operators in spherical coordinates since they incorrectly assume a flat geometry. To overcome this limitation, we generalize FNOs on the sphere, introducing Spherical FNOs (SFNOs) for learning operators on spherical geometries. We apply SFNOs to forecasting atmospheric dynamics, and demonstrate stable auto\-regressive rollouts for a year of simulated time (1,460 steps), while retaining physically plausible dynamics. The SFNO has important implications for machine learning-based simulation of climate dynamics that could eventually help accelerate our response to climate change.

$ν$-net: Deep Learning for Generalized Biventricular Cardiac Mass and Function Parameters

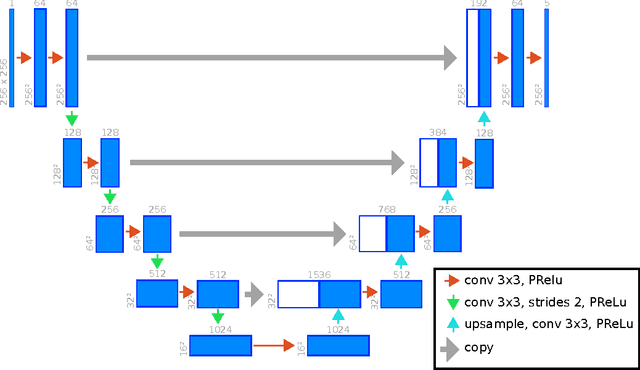
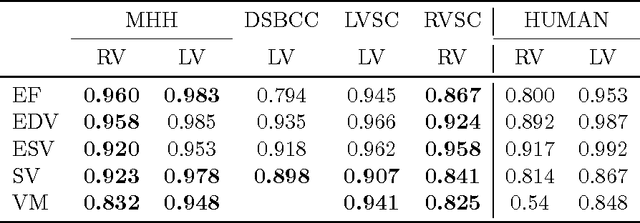
Background: Cardiac MRI derived biventricular mass and function parameters, such as end-systolic volume (ESV), end-diastolic volume (EDV), ejection fraction (EF), stroke volume (SV), and ventricular mass (VM) are clinically well established. Image segmentation can be challenging and time-consuming, due to the complex anatomy of the human heart. Objectives: This study introduces $\nu$-net (/nju:n$\varepsilon$t/) -- a deep learning approach allowing for fully-automated high quality segmentation of right (RV) and left ventricular (LV) endocardium and epicardium for extraction of cardiac function parameters. Methods: A set consisting of 253 manually segmented cases has been used to train a deep neural network. Subsequently, the network has been evaluated on 4 different multicenter data sets with a total of over 1000 cases. Results: For LV EF the intraclass correlation coefficient (ICC) is 98, 95, and 80 % (95 %), and for RV EF 96, and 87 % (80 %) on the respective data sets (human expert ICCs reported in parenthesis). The LV VM ICC is 95, and 94 % (84 %), and the RV VM ICC is 83, and 83 % (54 %). This study proposes a simple adjustment procedure, allowing for the adaptation to distinct segmentation philosophies. $\nu$-net exhibits state of-the-art performance in terms of dice coefficient. Conclusions: Biventricular mass and function parameters can be determined reliably in high quality by applying a deep neural network for cardiac MRI segmentation, especially in the anatomically complex right ventricle. Adaption to individual segmentation styles by applying a simple adjustment procedure is viable, allowing for the processing of novel data without time-consuming additional training.