Factorized Implicit Global Convolution for Automotive Computational Fluid Dynamics Prediction

Computational Fluid Dynamics (CFD) is crucial for automotive design, requiring the analysis of large 3D point clouds to study how vehicle geometry affects pressure fields and drag forces. However, existing deep learning approaches for CFD struggle with the computational complexity of processing high-resolution 3D data. We propose Factorized Implicit Global Convolution (FIGConv), a novel architecture that efficiently solves CFD problems for very large 3D meshes with arbitrary input and output geometries. FIGConv achieves quadratic complexity $O(N^2)$, a significant improvement over existing 3D neural CFD models that require cubic complexity $O(N^3)$. Our approach combines Factorized Implicit Grids to approximate high-resolution domains, efficient global convolutions through 2D reparameterization, and a U-shaped architecture for effective information gathering and integration. We validate our approach on the industry-standard Ahmed body dataset and the large-scale DrivAerNet dataset. In DrivAerNet, our model achieves an $R^2$ value of 0.95 for drag prediction, outperforming the previous state-of-the-art by a significant margin. This represents a 40% improvement in relative mean squared error and a 70% improvement in absolute mean squared error over previous methods.

Mosaic3D: Foundation Dataset and Model for Open-Vocabulary 3D Segmentation

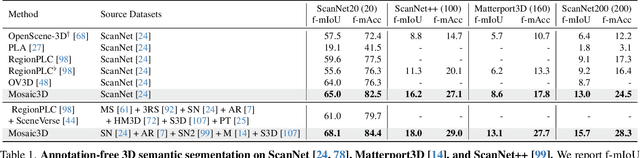
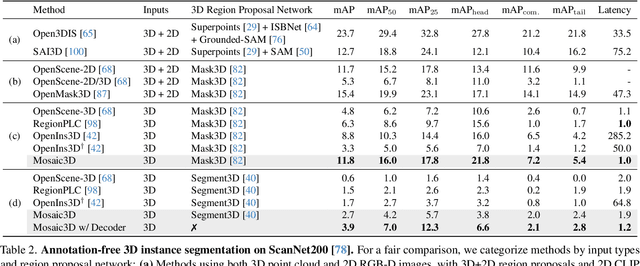
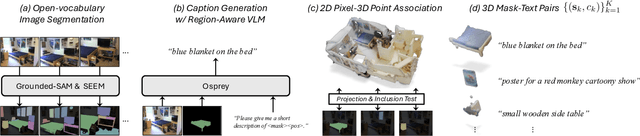
We tackle open-vocabulary 3D scene understanding by introducing a novel data generation pipeline and training framework. Our method addresses three critical requirements for effective training: precise 3D region segmentation, comprehensive textual descriptions, and sufficient dataset scale. By leveraging state-of-the-art open-vocabulary image segmentation models and region-aware Vision-Language Models, we develop an automatic pipeline that generates high-quality 3D mask-text pairs. Applying this pipeline to multiple 3D scene datasets, we create Mosaic3D-5.6M, a dataset of over 30K annotated scenes with 5.6M mask-text pairs, significantly larger than existing datasets. Building upon this data, we propose Mosaic3D, a foundation model combining a 3D encoder trained with contrastive learning and a lightweight mask decoder for open-vocabulary 3D semantic and instance segmentation. Our approach achieves state-of-the-art results on open-vocabulary 3D semantic and instance segmentation tasks including ScanNet200, Matterport3D, and ScanNet++, with ablation studies validating the effectiveness of our large-scale training data.

Improving Distant 3D Object Detection Using 2D Box Supervision

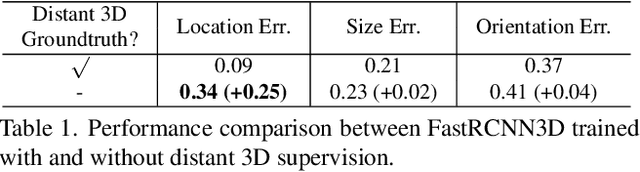
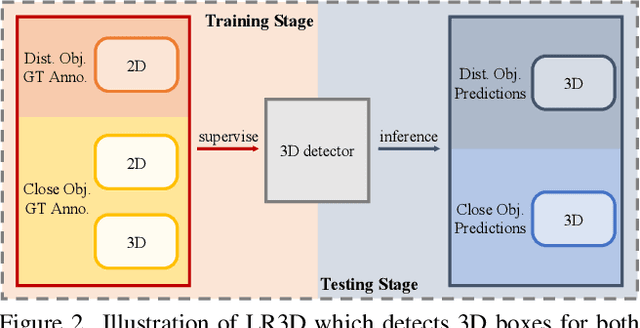
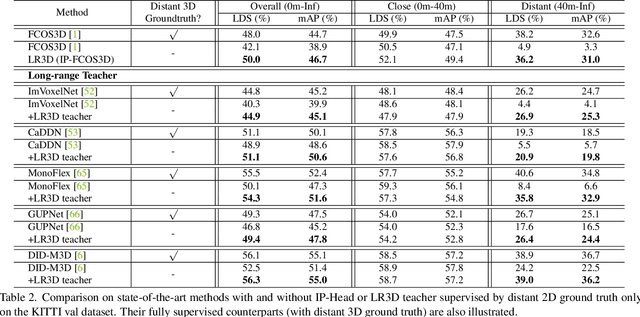
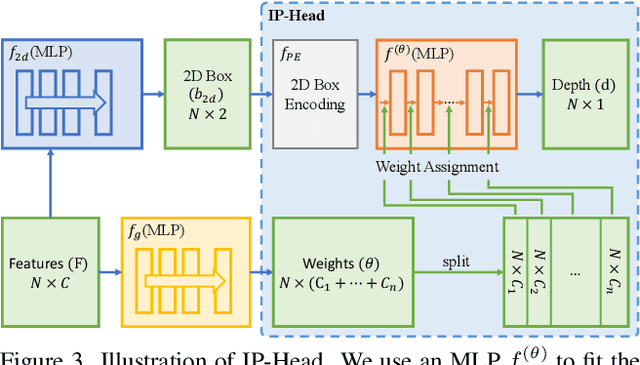
Improving the detection of distant 3d objects is an important yet challenging task. For camera-based 3D perception, the annotation of 3d bounding relies heavily on LiDAR for accurate depth information. As such, the distance of annotation is often limited due to the sparsity of LiDAR points on distant objects, which hampers the capability of existing detectors for long-range scenarios. We address this challenge by considering only 2D box supervision for distant objects since they are easy to annotate. We propose LR3D, a framework that learns to recover the missing depth of distant objects. LR3D adopts an implicit projection head to learn the generation of mapping between 2D boxes and depth using the 3D supervision on close objects. This mapping allows the depth estimation of distant objects conditioned on their 2D boxes, making long-range 3D detection with 2D supervision feasible. Experiments show that without distant 3D annotations, LR3D allows camera-based methods to detect distant objects (over 200m) with comparable accuracy to full 3D supervision. Our framework is general, and could widely benefit 3D detection methods to a large extent.

Geometry-Informed Neural Operator for Large-Scale 3D PDEs

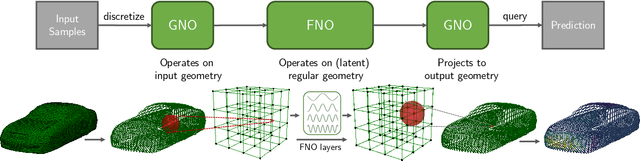
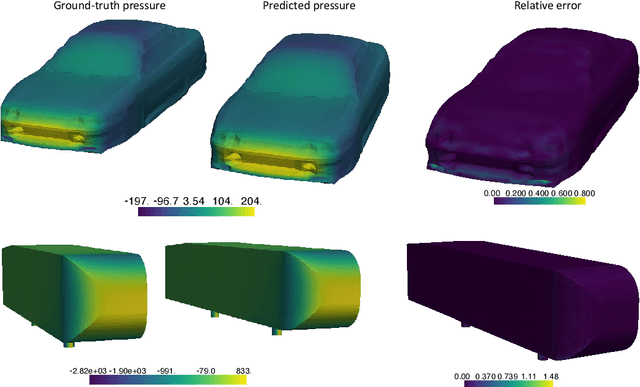
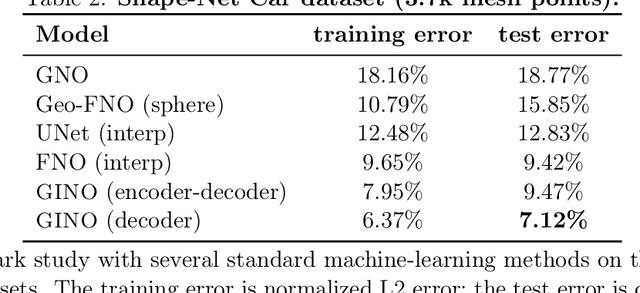
We propose the geometry-informed neural operator (GINO), a highly efficient approach to learning the solution operator of large-scale partial differential equations with varying geometries. GINO uses a signed distance function and point-cloud representations of the input shape and neural operators based on graph and Fourier architectures to learn the solution operator. The graph neural operator handles irregular grids and transforms them into and from regular latent grids on which Fourier neural operator can be efficiently applied. GINO is discretization-convergent, meaning the trained model can be applied to arbitrary discretization of the continuous domain and it converges to the continuum operator as the discretization is refined. To empirically validate the performance of our method on large-scale simulation, we generate the industry-standard aerodynamics dataset of 3D vehicle geometries with Reynolds numbers as high as five million. For this large-scale 3D fluid simulation, numerical methods are expensive to compute surface pressure. We successfully trained GINO to predict the pressure on car surfaces using only five hundred data points. The cost-accuracy experiments show a $26,000 \times$ speed-up compared to optimized GPU-based computational fluid dynamics (CFD) simulators on computing the drag coefficient. When tested on new combinations of geometries and boundary conditions (inlet velocities), GINO obtains a one-fourth reduction in error rate compared to deep neural network approaches.

Fast Monocular Scene Reconstruction with Global-Sparse Local-Dense Grids

Indoor scene reconstruction from monocular images has long been sought after by augmented reality and robotics developers. Recent advances in neural field representations and monocular priors have led to remarkable results in scene-level surface reconstructions. The reliance on Multilayer Perceptrons (MLP), however, significantly limits speed in training and rendering. In this work, we propose to directly use signed distance function (SDF) in sparse voxel block grids for fast and accurate scene reconstruction without MLPs. Our globally sparse and locally dense data structure exploits surfaces' spatial sparsity, enables cache-friendly queries, and allows direct extensions to multi-modal data such as color and semantic labels. To apply this representation to monocular scene reconstruction, we develop a scale calibration algorithm for fast geometric initialization from monocular depth priors. We apply differentiable volume rendering from this initialization to refine details with fast convergence. We also introduce efficient high-dimensional Continuous Random Fields (CRFs) to further exploit the semantic-geometry consistency between scene objects. Experiments show that our approach is 10x faster in training and 100x faster in rendering while achieving comparable accuracy to state-of-the-art neural implicit methods.