X-MeshGraphNet: Scalable Multi-Scale Graph Neural Networks for Physics Simulation

Graph Neural Networks (GNNs) have gained significant traction for simulating complex physical systems, with models like MeshGraphNet demonstrating strong performance on unstructured simulation meshes. However, these models face several limitations, including scalability issues, requirement for meshing at inference, and challenges in handling long-range interactions. In this work, we introduce X-MeshGraphNet, a scalable, multi-scale extension of MeshGraphNet designed to address these challenges. X-MeshGraphNet overcomes the scalability bottleneck by partitioning large graphs and incorporating halo regions that enable seamless message passing across partitions. This, combined with gradient aggregation, ensures that training across partitions is equivalent to processing the entire graph at once. To remove the dependency on simulation meshes, X-MeshGraphNet constructs custom graphs directly from CAD files by generating uniform point clouds on the surface or volume of the object and connecting k-nearest neighbors. Additionally, our model builds multi-scale graphs by iteratively combining coarse and fine-resolution point clouds, where each level refines the previous, allowing for efficient long-range interactions. Our experiments demonstrate that X-MeshGraphNet maintains the predictive accuracy of full-graph GNNs while significantly improving scalability and flexibility. This approach eliminates the need for time-consuming mesh generation at inference, offering a practical solution for real-time simulation across a wide range of applications. The code for reproducing the results presented in this paper is available through NVIDIA Modulus: github.com/NVIDIA/modulus/tree/main/examples/cfd/xaeronet.

Virtual Foundry Graphnet for Metal Sintering Deformation Prediction

Metal Sintering is a necessary step for Metal Injection Molded parts and binder jet such as HP's metal 3D printer. The metal sintering process introduces large deformation varying from 25 to 50% depending on the green part porosity. In this paper, we use a graph-based deep learning approach to predict the part deformation, which can speed up the deformation simulation substantially at the voxel level. Running a well-trained Metal Sintering inferencing engine only takes a range of seconds to obtain the final sintering deformation value. The tested accuracy on example complex geometry achieves 0.7um mean deviation for a 63mm testing part.

Geometry-Informed Neural Operator for Large-Scale 3D PDEs

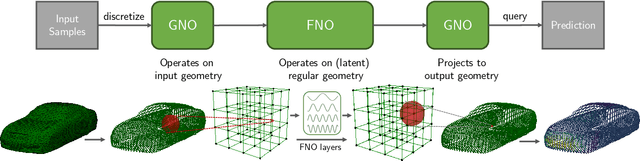
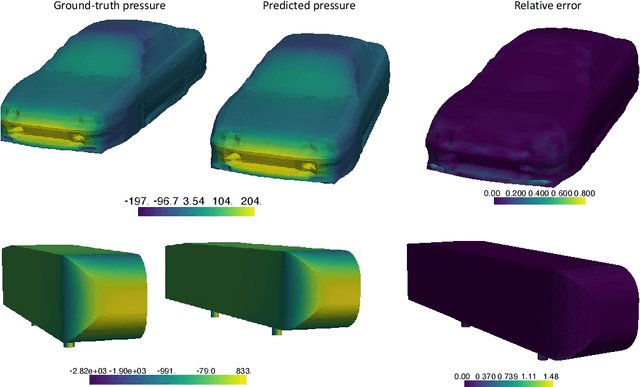
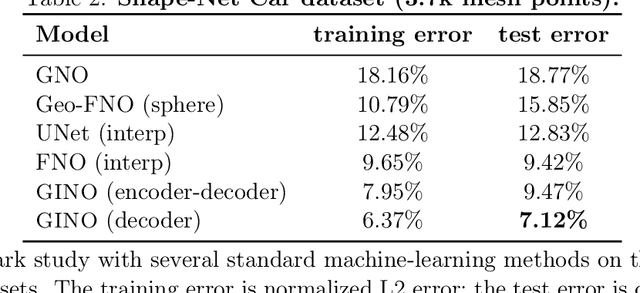
We propose the geometry-informed neural operator (GINO), a highly efficient approach to learning the solution operator of large-scale partial differential equations with varying geometries. GINO uses a signed distance function and point-cloud representations of the input shape and neural operators based on graph and Fourier architectures to learn the solution operator. The graph neural operator handles irregular grids and transforms them into and from regular latent grids on which Fourier neural operator can be efficiently applied. GINO is discretization-convergent, meaning the trained model can be applied to arbitrary discretization of the continuous domain and it converges to the continuum operator as the discretization is refined. To empirically validate the performance of our method on large-scale simulation, we generate the industry-standard aerodynamics dataset of 3D vehicle geometries with Reynolds numbers as high as five million. For this large-scale 3D fluid simulation, numerical methods are expensive to compute surface pressure. We successfully trained GINO to predict the pressure on car surfaces using only five hundred data points. The cost-accuracy experiments show a $26,000 \times$ speed-up compared to optimized GPU-based computational fluid dynamics (CFD) simulators on computing the drag coefficient. When tested on new combinations of geometries and boundary conditions (inlet velocities), GINO obtains a one-fourth reduction in error rate compared to deep neural network approaches.

Robust Topology Optimization Using Variational Autoencoders

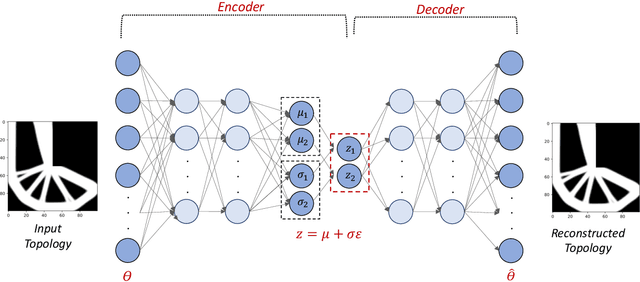
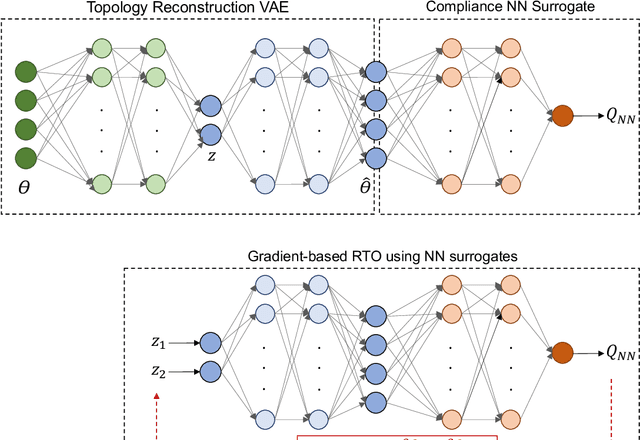
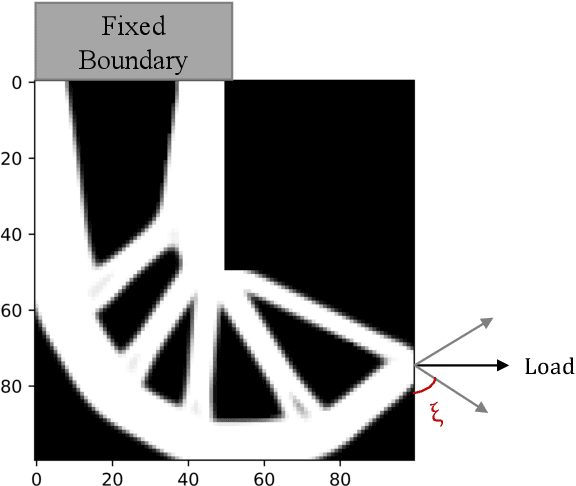
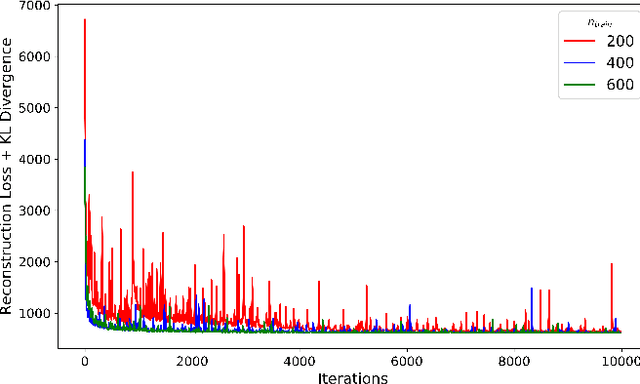
Topology Optimization is the process of finding the optimal arrangement of materials within a design domain by minimizing a cost function, subject to some performance constraints. Robust topology optimization (RTO) also incorporates the effect of input uncertainties and produces a design with the best average performance of the structure while reducing the response sensitivity to input uncertainties. It is computationally expensive to carry out RTO using finite element and Monte Carlo sampling. In this work, we use neural network surrogates to enable a faster solution approach via surrogate-based optimization and build a Variational Autoencoder (VAE) to transform the the high dimensional design space into a low dimensional one. Furthermore, finite element solvers will be replaced by a neural network surrogate. Also, to further facilitate the design exploration, we limit our search to a subspace, which consists of designs that are solutions to deterministic topology optimization problems under different realizations of input uncertainties. With these neural network approximations, a gradient-based optimization approach is formed to minimize the predicted objective function over the low dimensional design subspace. We demonstrate the effectiveness of the proposed approach on two compliance minimization problems and show that VAE performs well on learning the features of the design from minimal training data, and that converting the design space into a low dimensional latent space makes the problem computationally efficient. The resulting gradient-based optimization algorithm produces optimal designs with lower robust compliances than those observed in the training set.

Efficient training of physics-informed neural networks via importance sampling

Physics-Informed Neural Networks (PINNs) are a class of deep neural networks that are trained, using automatic differentiation, to compute the response of systems governed by partial differential equations (PDEs). The training of PINNs is simulation-free, and does not require any training dataset to be obtained from numerical PDE solvers. Instead, it only requires the physical problem description, including the governing laws of physics, domain geometry, initial/boundary conditions, and the material properties. This training usually involves solving a non-convex optimization problem using variants of the stochastic gradient descent method, with the gradient of the loss function approximated on a batch of collocation points, selected randomly in each iteration according to a uniform distribution. Despite the success of PINNs in accurately solving a wide variety of PDEs, the method still requires improvements in terms of computational efficiency. To this end, in this paper, we study the performance of an importance sampling approach for efficient training of PINNs. Using numerical examples together with theoretical evidences, we show that in each training iteration, sampling the collocation points according to a distribution proportional to the loss function will improve the convergence behavior of the PINNs training. Additionally, we show that providing a piecewise constant approximation to the loss function for faster importance sampling can further improve the training efficiency. This importance sampling approach is straightforward and easy to implement in the existing PINN codes, and also does not introduce any new hyperparameter to calibrate. The numerical examples include elasticity, diffusion and plane stress problems, through which we numerically verify the accuracy and efficiency of the importance sampling approach compared to the predominant uniform sampling approach.

NVIDIA SimNet^{TM}: an AI-accelerated multi-physics simulation framework

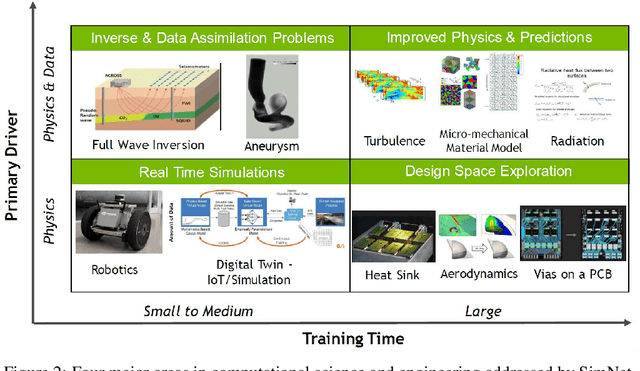
We present SimNet, an AI-driven multi-physics simulation framework, to accelerate simulations across a wide range of disciplines in science and engineering. Compared to traditional numerical solvers, SimNet addresses a wide range of use cases - coupled forward simulations without any training data, inverse and data assimilation problems. SimNet offers fast turnaround time by enabling parameterized system representation that solves for multiple configurations simultaneously, as opposed to the traditional solvers that solve for one configuration at a time. SimNet is integrated with parameterized constructive solid geometry as well as STL modules to generate point clouds. Furthermore, it is customizable with APIs that enable user extensions to geometry, physics and network architecture. It has advanced network architectures that are optimized for high-performance GPU computing, and offers scalable performance for multi-GPU and multi-Node implementation with accelerated linear algebra as well as FP32, FP64 and TF32 computations. In this paper we review the neural network solver methodology, the SimNet architecture, and the various features that are needed for effective solution of the PDEs. We present real-world use cases that range from challenging forward multi-physics simulations with turbulence and complex 3D geometries, to industrial design optimization and inverse problems that are not addressed efficiently by the traditional solvers. Extensive comparisons of SimNet results with open source and commercial solvers show good correlation.

Adaptive Physics-Informed Neural Networks for Markov-Chain Monte Carlo

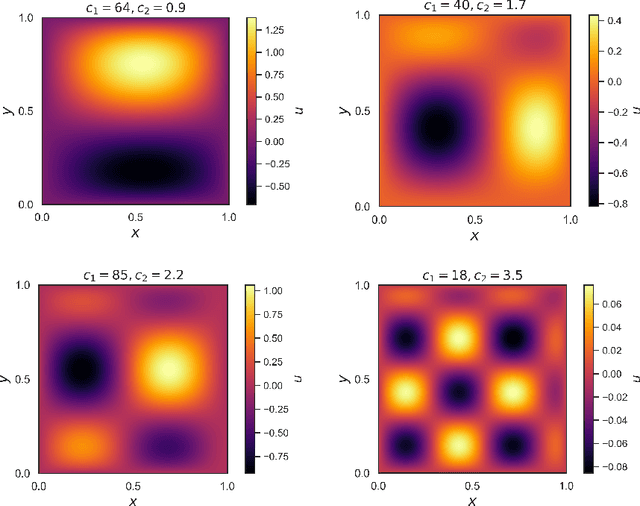
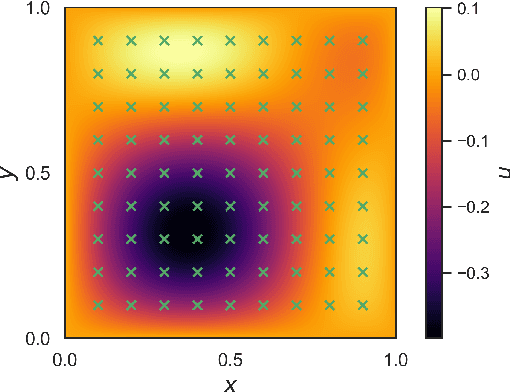
In this paper, we propose the Adaptive Physics-Informed Neural Networks (APINNs) for accurate and efficient simulation-free Bayesian parameter estimation via Markov-Chain Monte Carlo (MCMC). We specifically focus on a class of parameter estimation problems for which computing the likelihood function requires solving a PDE. The proposed method consists of: (1) constructing an offline PINN-UQ model as an approximation to the forward model; and (2) refining this approximate model on the fly using samples generated from the MCMC sampler. The proposed APINN method constantly refines this approximate model on the fly and guarantees that the approximation error is always less than a user-defined residual error threshold. We numerically demonstrate the performance of the proposed APINN method in solving a parameter estimation problem for a system governed by the Poisson equation.

Physics-Informed Regularization of Deep Neural Networks

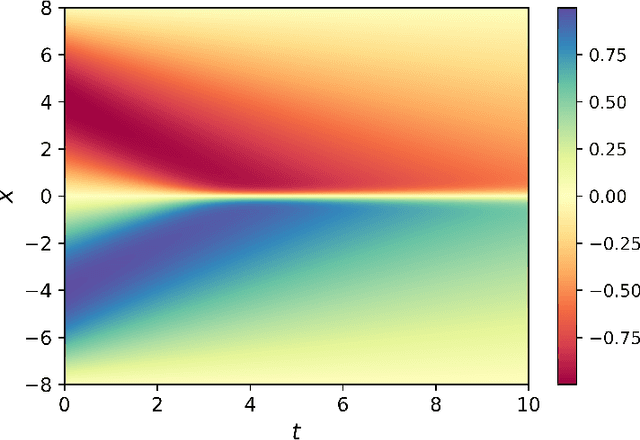
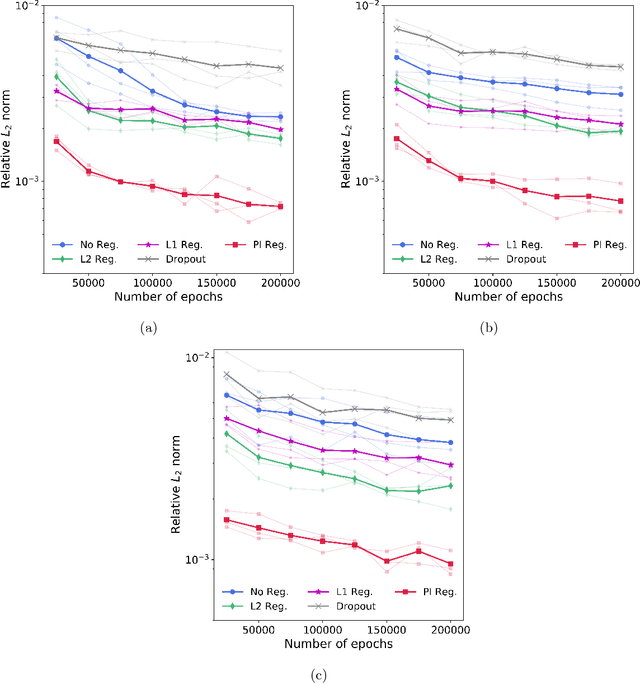
This paper presents a novel physics-informed regularization method for training of deep neural networks (DNNs). In particular, we focus on the DNN representation for the response of a physical or biological system, for which a set of governing laws are known. These laws often appear in the form of differential equations, derived from first principles, empirically-validated laws, and/or domain expertise. We propose a DNN training approach that utilizes these known differential equations in addition to the measurement data, by introducing a penalty term to the training loss function to penalize divergence form the governing laws. Through three numerical examples, we will show that the proposed regularization produces surrogates that are physically interpretable with smaller generalization errors, when compared to other common regularization methods.

A Deep Neural Network Surrogate for High-Dimensional Random Partial Differential Equations

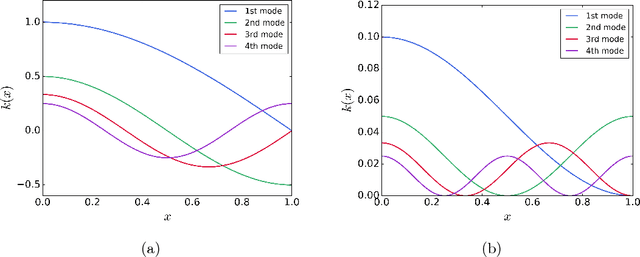
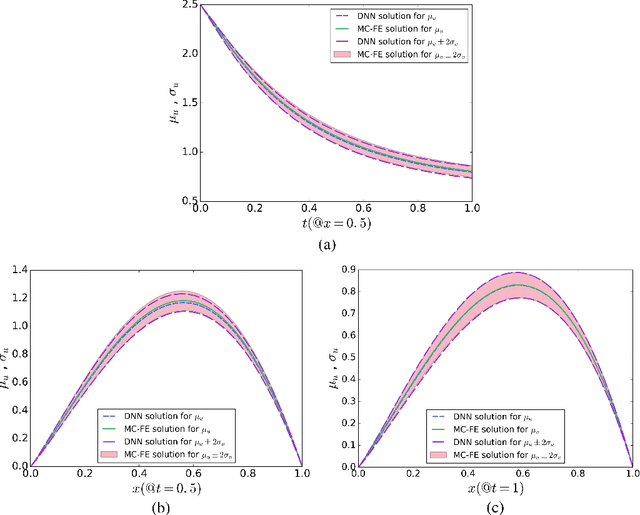
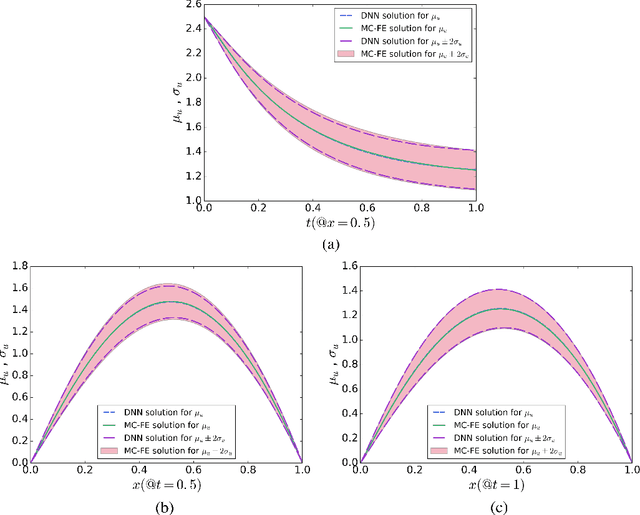
Developing efficient numerical algorithms for the solution of high dimensional random Partial Differential Equations (PDEs) has been a challenging task due to the well-known curse of dimensionality. We present a new solution framework for these problems based on a deep learning approach. Specifically, the random PDE is approximated by a feed-forward fully-connected deep residual network, with either strong or weak enforcement of initial and boundary constraints. The framework is mesh-free, and can handle irregular computational domains. Parameters of the approximating deep neural network are determined iteratively using variants of the Stochastic Gradient Descent (SGD) algorithm. The satisfactory accuracy of the proposed frameworks is numerically demonstrated on diffusion and heat conduction problems, in comparison with the converged Monte Carlo-based finite element results.

Deep Learning for Accelerated Reliability Analysis of Infrastructure Networks

Natural disasters can have catastrophic impacts on the functionality of infrastructure systems and cause severe physical and socio-economic losses. Given budget constraints, it is crucial to optimize decisions regarding mitigation, preparedness, response, and recovery practices for these systems. This requires accurate and efficient means to evaluate the infrastructure system reliability. While numerous research efforts have addressed and quantified the impact of natural disasters on infrastructure systems, typically using the Monte Carlo approach, they still suffer from high computational cost and, thus, are of limited applicability to large systems. This paper presents a deep learning framework for accelerating infrastructure system reliability analysis. In particular, two distinct deep neural network surrogates are constructed and studied: (1) A classifier surrogate which speeds up the connectivity determination of networks, and (2) An end-to-end surrogate that replaces a number of components such as roadway status realization, connectivity determination, and connectivity averaging. The proposed approach is applied to a simulation-based study of the two-terminal connectivity of a California transportation network subject to extreme probabilistic earthquake events. Numerical results highlight the effectiveness of the proposed approach in accelerating the transportation system two-terminal reliability analysis with extremely high prediction accuracy.