Learning Functional Priors and Posteriors from Data and Physics

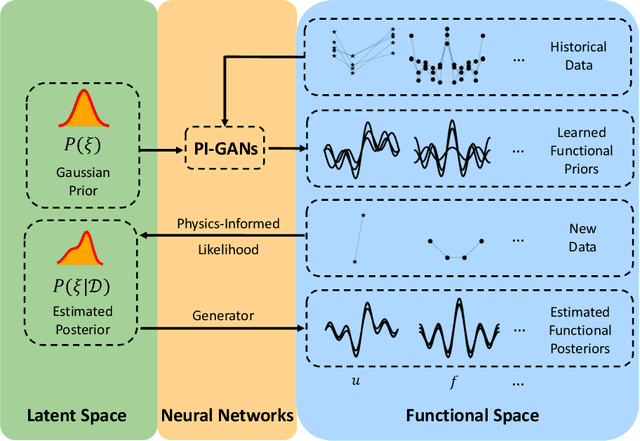
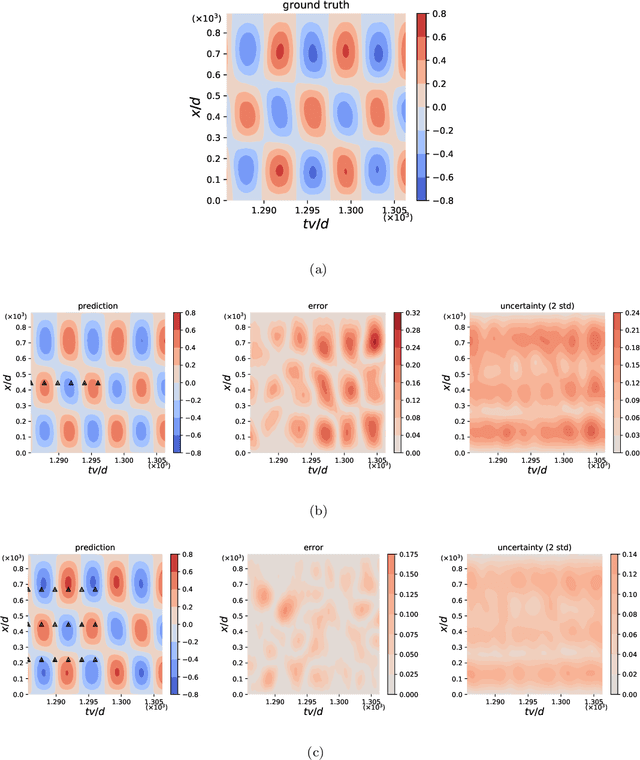
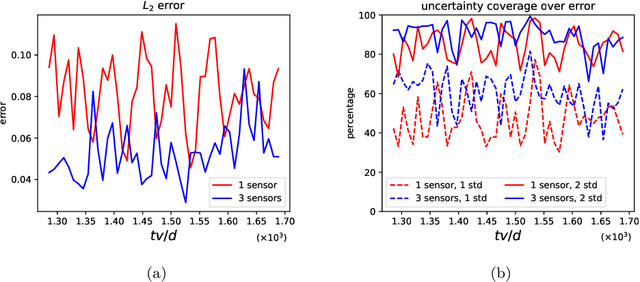
We develop a new Bayesian framework based on deep neural networks to be able to extrapolate in space-time using historical data and to quantify uncertainties arising from both noisy and gappy data in physical problems. Specifically, the proposed approach has two stages: (1) prior learning and (2) posterior estimation. At the first stage, we employ the physics-informed Generative Adversarial Networks (PI-GAN) to learn a functional prior either from a prescribed function distribution, e.g., Gaussian process, or from historical data and physics. At the second stage, we employ the Hamiltonian Monte Carlo (HMC) method to estimate the posterior in the latent space of PI-GANs. In addition, we use two different approaches to encode the physics: (1) automatic differentiation, used in the physics-informed neural networks (PINNs) for scenarios with explicitly known partial differential equations (PDEs), and (2) operator regression using the deep operator network (DeepONet) for PDE-agnostic scenarios. We then test the proposed method for (1) meta-learning for one-dimensional regression, and forward/inverse PDE problems (combined with PINNs); (2) PDE-agnostic physical problems (combined with DeepONet), e.g., fractional diffusion as well as saturated stochastic (100-dimensional) flows in heterogeneous porous media; and (3) spatial-temporal regression problems, i.e., inference of a marine riser displacement field. The results demonstrate that the proposed approach can provide accurate predictions as well as uncertainty quantification given very limited scattered and noisy data, since historical data could be available to provide informative priors. In summary, the proposed method is capable of learning flexible functional priors, and can be extended to big data problems using stochastic HMC or normalizing flows since the latent space is generally characterized as low dimensional.

NVIDIA SimNet^{TM}: an AI-accelerated multi-physics simulation framework

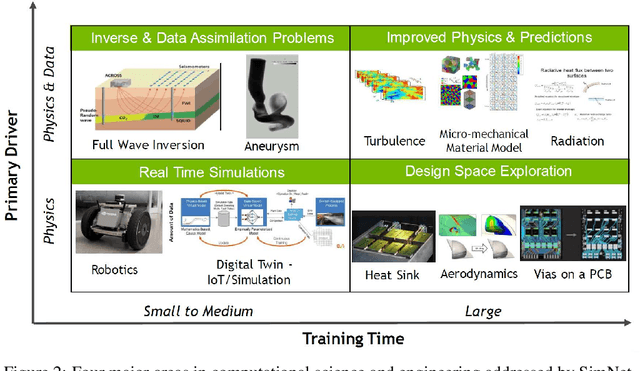
We present SimNet, an AI-driven multi-physics simulation framework, to accelerate simulations across a wide range of disciplines in science and engineering. Compared to traditional numerical solvers, SimNet addresses a wide range of use cases - coupled forward simulations without any training data, inverse and data assimilation problems. SimNet offers fast turnaround time by enabling parameterized system representation that solves for multiple configurations simultaneously, as opposed to the traditional solvers that solve for one configuration at a time. SimNet is integrated with parameterized constructive solid geometry as well as STL modules to generate point clouds. Furthermore, it is customizable with APIs that enable user extensions to geometry, physics and network architecture. It has advanced network architectures that are optimized for high-performance GPU computing, and offers scalable performance for multi-GPU and multi-Node implementation with accelerated linear algebra as well as FP32, FP64 and TF32 computations. In this paper we review the neural network solver methodology, the SimNet architecture, and the various features that are needed for effective solution of the PDEs. We present real-world use cases that range from challenging forward multi-physics simulations with turbulence and complex 3D geometries, to industrial design optimization and inverse problems that are not addressed efficiently by the traditional solvers. Extensive comparisons of SimNet results with open source and commercial solvers show good correlation.