Xuhui Meng
Uncertainty quantification for noisy inputs-outputs in physics-informed neural networks and neural operators
Nov 19, 2023



Abstract:Uncertainty quantification (UQ) in scientific machine learning (SciML) becomes increasingly critical as neural networks (NNs) are being widely adopted in addressing complex problems across various scientific disciplines. Representative SciML models are physics-informed neural networks (PINNs) and neural operators (NOs). While UQ in SciML has been increasingly investigated in recent years, very few works have focused on addressing the uncertainty caused by the noisy inputs, such as spatial-temporal coordinates in PINNs and input functions in NOs. The presence of noise in the inputs of the models can pose significantly more challenges compared to noise in the outputs of the models, primarily due to the inherent nonlinearity of most SciML algorithms. As a result, UQ for noisy inputs becomes a crucial factor for reliable and trustworthy deployment of these models in applications involving physical knowledge. To this end, we introduce a Bayesian approach to quantify uncertainty arising from noisy inputs-outputs in PINNs and NOs. We show that this approach can be seamlessly integrated into PINNs and NOs, when they are employed to encode the physical information. PINNs incorporate physics by including physics-informed terms via automatic differentiation, either in the loss function or the likelihood, and often take as input the spatial-temporal coordinate. Therefore, the present method equips PINNs with the capability to address problems where the observed coordinate is subject to noise. On the other hand, pretrained NOs are also commonly employed as equation-free surrogates in solving differential equations and Bayesian inverse problems, in which they take functions as inputs. The proposed approach enables them to handle noisy measurements for both input and output functions with UQ.
Correcting model misspecification in physics-informed neural networks (PINNs)
Oct 16, 2023



Abstract:Data-driven discovery of governing equations in computational science has emerged as a new paradigm for obtaining accurate physical models and as a possible alternative to theoretical derivations. The recently developed physics-informed neural networks (PINNs) have also been employed to learn governing equations given data across diverse scientific disciplines. Despite the effectiveness of PINNs for discovering governing equations, the physical models encoded in PINNs may be misspecified in complex systems as some of the physical processes may not be fully understood, leading to the poor accuracy of PINN predictions. In this work, we present a general approach to correct the misspecified physical models in PINNs for discovering governing equations, given some sparse and/or noisy data. Specifically, we first encode the assumed physical models, which may be misspecified, then employ other deep neural networks (DNNs) to model the discrepancy between the imperfect models and the observational data. Due to the expressivity of DNNs, the proposed method is capable of reducing the computational errors caused by the model misspecification and thus enables the applications of PINNs in complex systems where the physical processes are not exactly known. Furthermore, we utilize the Bayesian PINNs (B-PINNs) and/or ensemble PINNs to quantify uncertainties arising from noisy and/or gappy data in the discovered governing equations. A series of numerical examples including non-Newtonian channel and cavity flows demonstrate that the added DNNs are capable of correcting the model misspecification in PINNs and thus reduce the discrepancy between the physical models and the observational data. We envision that the proposed approach will extend the applications of PINNs for discovering governing equations in problems where the physico-chemical or biological processes are not well understood.
Physics-informed neural networks for predicting gas flow dynamics and unknown parameters in diesel engines
Apr 26, 2023Abstract:This paper presents a physics-informed neural network (PINN) approach for monitoring the health of diesel engines. The aim is to evaluate the engine dynamics, identify unknown parameters in a "mean value" model, and anticipate maintenance requirements. The PINN model is applied to diesel engines with a variable-geometry turbocharger and exhaust gas recirculation, using measurement data of selected state variables. The results demonstrate the ability of the PINN model to predict simultaneously both unknown parameters and dynamics accurately with both clean and noisy data, and the importance of the self-adaptive weight in the loss function for faster convergence. The input data for these simulations are derived from actual engine running conditions, while the outputs are simulated data, making this a practical case study of PINN's ability to predict real-world dynamical systems. The mean value model of the diesel engine incorporates empirical formulae to represent certain states, but these formulae may not be generalizable to other engines. To address this, the study considers the use of deep neural networks (DNNs) in addition to the PINN model. The DNNs are trained using laboratory test data and are used to model the engine-specific empirical formulae in the mean value model, allowing for a more flexible and adaptive representation of the engine's states. In other words, the mean value model uses both the PINN model and the DNNs to represent the engine's states, with the PINN providing a physics-based understanding of the engine's overall dynamics and the DNNs offering a more engine-specific and adaptive representation of the empirical formulae. By combining these two approaches, the study aims to offer a comprehensive and versatile approach to monitoring the health and performance of diesel engines.
Deep neural operator for learning transient response of interpenetrating phase composites subject to dynamic loading
Mar 30, 2023Abstract:Additive manufacturing has been recognized as an industrial technological revolution for manufacturing, which allows fabrication of materials with complex three-dimensional (3D) structures directly from computer-aided design models. The mechanical properties of interpenetrating phase composites (IPCs), especially response to dynamic loading, highly depend on their 3D structures. In general, for each specified structural design, it could take hours or days to perform either finite element analysis (FEA) or experiments to test the mechanical response of IPCs to a given dynamic load. To accelerate the physics-based prediction of mechanical properties of IPCs for various structural designs, we employ a deep neural operator (DNO) to learn the transient response of IPCs under dynamic loading as surrogate of physics-based FEA models. We consider a 3D IPC beam formed by two metals with a ratio of Young's modulus of 2.7, wherein random blocks of constituent materials are used to demonstrate the generality and robustness of the DNO model. To obtain FEA results of IPC properties, 5,000 random time-dependent strain loads generated by a Gaussian process kennel are applied to the 3D IPC beam, and the reaction forces and stress fields inside the IPC beam under various loading are collected. Subsequently, the DNO model is trained using an incremental learning method with sequence-to-sequence training implemented in JAX, leading to a 100X speedup compared to widely used vanilla deep operator network models. After an offline training, the DNO model can act as surrogate of physics-based FEA to predict the transient mechanical response in terms of reaction force and stress distribution of the IPCs to various strain loads in one second at an accuracy of 98%. Also, the learned operator is able to provide extended prediction of the IPC beam subject to longer random strain loads at a reasonably well accuracy.
NeuralUQ: A comprehensive library for uncertainty quantification in neural differential equations and operators
Aug 25, 2022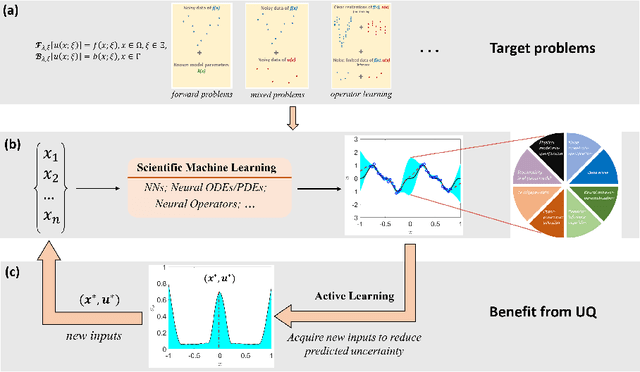

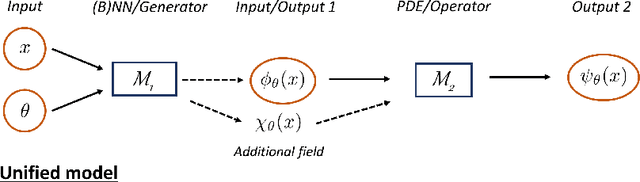
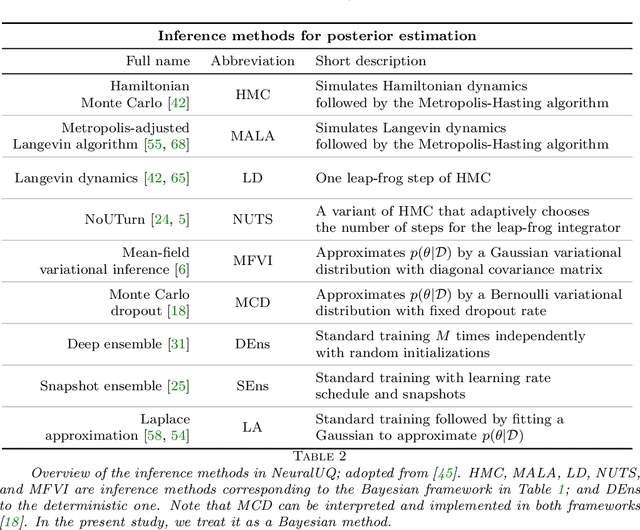
Abstract:Uncertainty quantification (UQ) in machine learning is currently drawing increasing research interest, driven by the rapid deployment of deep neural networks across different fields, such as computer vision, natural language processing, and the need for reliable tools in risk-sensitive applications. Recently, various machine learning models have also been developed to tackle problems in the field of scientific computing with applications to computational science and engineering (CSE). Physics-informed neural networks and deep operator networks are two such models for solving partial differential equations and learning operator mappings, respectively. In this regard, a comprehensive study of UQ methods tailored specifically for scientific machine learning (SciML) models has been provided in [45]. Nevertheless, and despite their theoretical merit, implementations of these methods are not straightforward, especially in large-scale CSE applications, hindering their broad adoption in both research and industry settings. In this paper, we present an open-source Python library (https://github.com/Crunch-UQ4MI), termed NeuralUQ and accompanied by an educational tutorial, for employing UQ methods for SciML in a convenient and structured manner. The library, designed for both educational and research purposes, supports multiple modern UQ methods and SciML models. It is based on a succinct workflow and facilitates flexible employment and easy extensions by the users. We first present a tutorial of NeuralUQ and subsequently demonstrate its applicability and efficiency in four diverse examples, involving dynamical systems and high-dimensional parametric and time-dependent PDEs.
Bayesian Physics-Informed Neural Networks for real-world nonlinear dynamical systems
May 12, 2022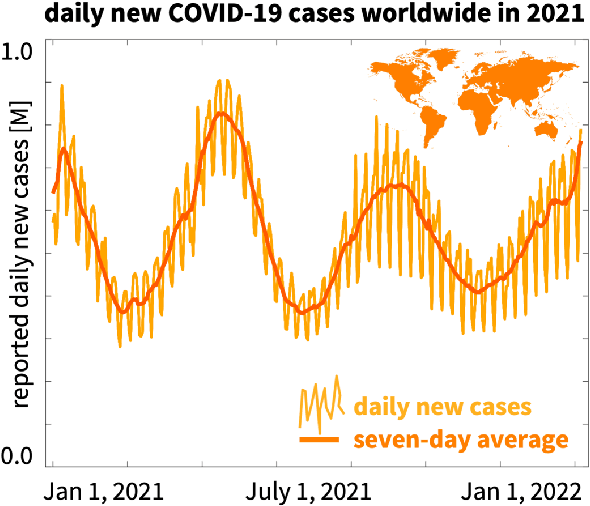
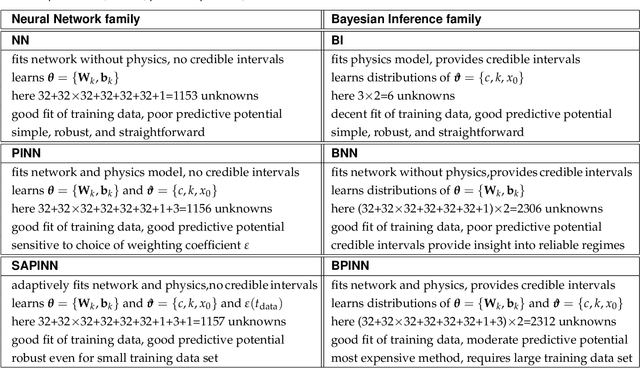

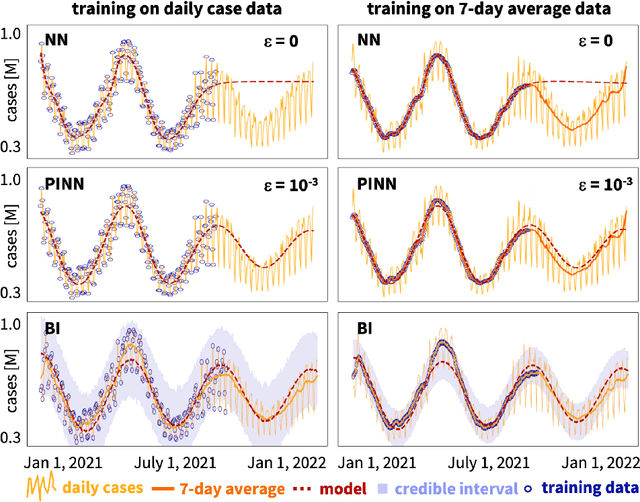
Abstract:Understanding real-world dynamical phenomena remains a challenging task. Across various scientific disciplines, machine learning has advanced as the go-to technology to analyze nonlinear dynamical systems, identify patterns in big data, and make decision around them. Neural networks are now consistently used as universal function approximators for data with underlying mechanisms that are incompletely understood or exceedingly complex. However, neural networks alone ignore the fundamental laws of physics and often fail to make plausible predictions. Here we integrate data, physics, and uncertainties by combining neural networks, physics-informed modeling, and Bayesian inference to improve the predictive potential of traditional neural network models. We embed the physical model of a damped harmonic oscillator into a fully-connected feed-forward neural network to explore a simple and illustrative model system, the outbreak dynamics of COVID-19. Our Physics-Informed Neural Networks can seamlessly integrate data and physics, robustly solve forward and inverse problems, and perform well for both interpolation and extrapolation, even for a small amount of noisy and incomplete data. At only minor additional cost, they can self-adaptively learn the weighting between data and physics. Combined with Bayesian Neural Networks, they can serve as priors in a Bayesian Inference, and provide credible intervals for uncertainty quantification. Our study reveals the inherent advantages and disadvantages of Neural Networks, Bayesian Inference, and a combination of both and provides valuable guidelines for model selection. While we have only demonstrated these approaches for the simple model problem of a seasonal endemic infectious disease, we anticipate that the underlying concepts and trends generalize to more complex disease conditions and, more broadly, to a wide variety of nonlinear dynamical systems.
Uncertainty Quantification in Scientific Machine Learning: Methods, Metrics, and Comparisons
Jan 19, 2022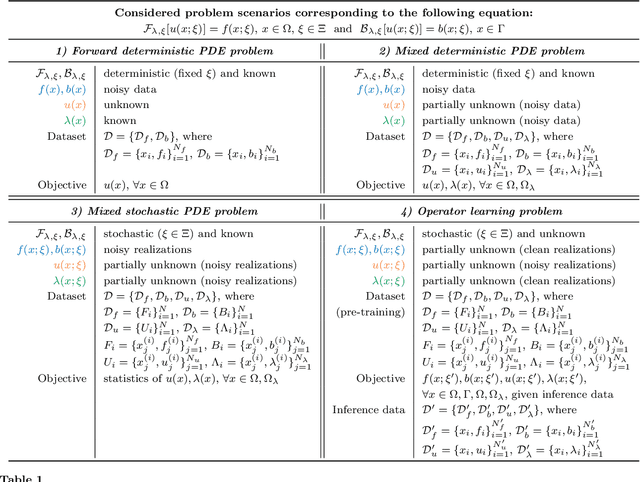

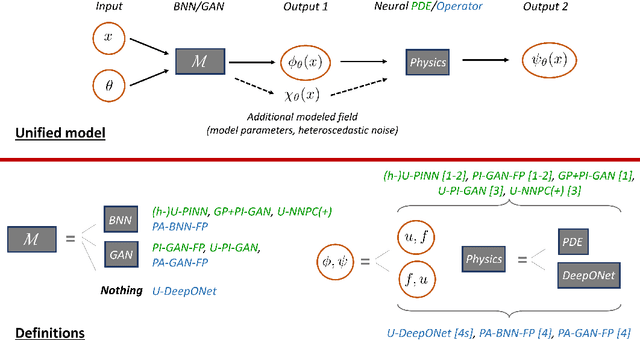
Abstract:Neural networks (NNs) are currently changing the computational paradigm on how to combine data with mathematical laws in physics and engineering in a profound way, tackling challenging inverse and ill-posed problems not solvable with traditional methods. However, quantifying errors and uncertainties in NN-based inference is more complicated than in traditional methods. This is because in addition to aleatoric uncertainty associated with noisy data, there is also uncertainty due to limited data, but also due to NN hyperparameters, overparametrization, optimization and sampling errors as well as model misspecification. Although there are some recent works on uncertainty quantification (UQ) in NNs, there is no systematic investigation of suitable methods towards quantifying the total uncertainty effectively and efficiently even for function approximation, and there is even less work on solving partial differential equations and learning operator mappings between infinite-dimensional function spaces using NNs. In this work, we present a comprehensive framework that includes uncertainty modeling, new and existing solution methods, as well as evaluation metrics and post-hoc improvement approaches. To demonstrate the applicability and reliability of our framework, we present an extensive comparative study in which various methods are tested on prototype problems, including problems with mixed input-output data, and stochastic problems in high dimensions. In the Appendix, we include a comprehensive description of all the UQ methods employed, which we will make available as open-source library of all codes included in this framework.
Gradient-enhanced physics-informed neural networks for forward and inverse PDE problems
Nov 01, 2021



Abstract:Deep learning has been shown to be an effective tool in solving partial differential equations (PDEs) through physics-informed neural networks (PINNs). PINNs embed the PDE residual into the loss function of the neural network, and have been successfully employed to solve diverse forward and inverse PDE problems. However, one disadvantage of the first generation of PINNs is that they usually have limited accuracy even with many training points. Here, we propose a new method, gradient-enhanced physics-informed neural networks (gPINNs), for improving the accuracy and training efficiency of PINNs. gPINNs leverage gradient information of the PDE residual and embed the gradient into the loss function. We tested gPINNs extensively and demonstrated the effectiveness of gPINNs in both forward and inverse PDE problems. Our numerical results show that gPINN performs better than PINN with fewer training points. Furthermore, we combined gPINN with the method of residual-based adaptive refinement (RAR), a method for improving the distribution of training points adaptively during training, to further improve the performance of gPINN, especially in PDEs with solutions that have steep gradients.
Learning Functional Priors and Posteriors from Data and Physics
Jun 08, 2021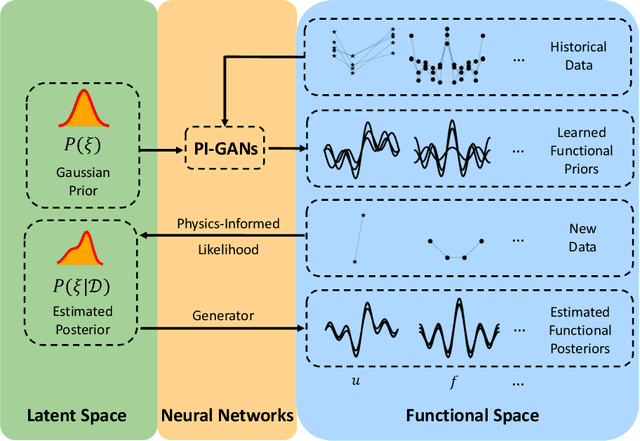
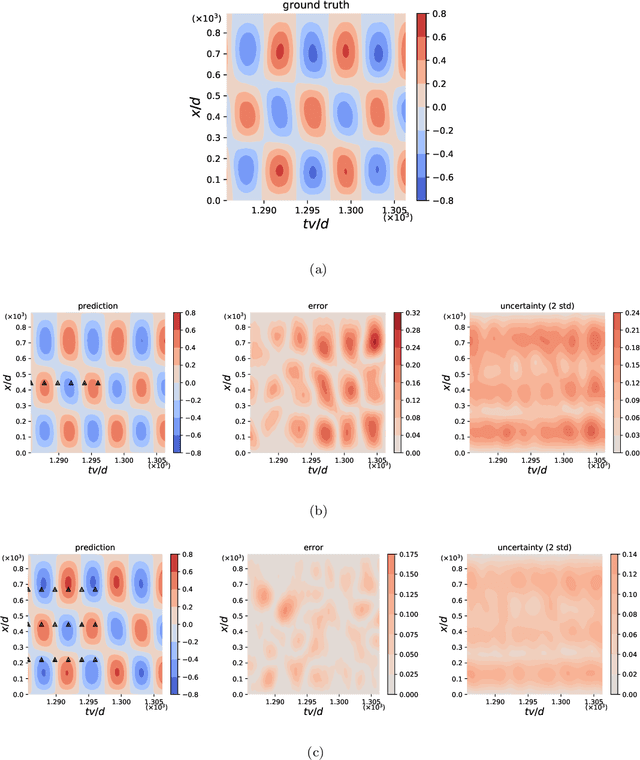
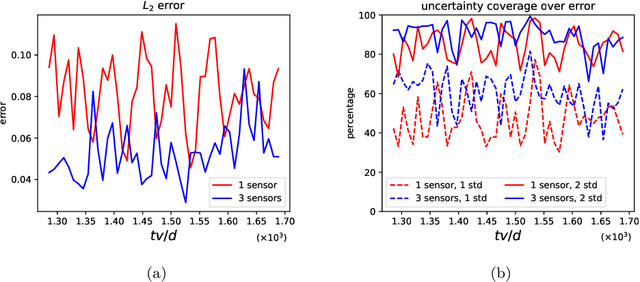

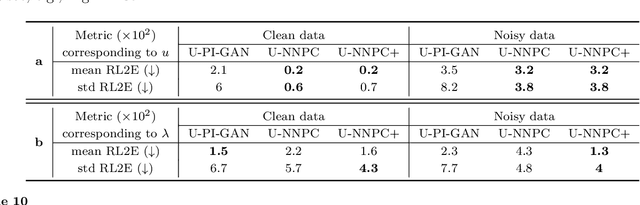
Abstract:We develop a new Bayesian framework based on deep neural networks to be able to extrapolate in space-time using historical data and to quantify uncertainties arising from both noisy and gappy data in physical problems. Specifically, the proposed approach has two stages: (1) prior learning and (2) posterior estimation. At the first stage, we employ the physics-informed Generative Adversarial Networks (PI-GAN) to learn a functional prior either from a prescribed function distribution, e.g., Gaussian process, or from historical data and physics. At the second stage, we employ the Hamiltonian Monte Carlo (HMC) method to estimate the posterior in the latent space of PI-GANs. In addition, we use two different approaches to encode the physics: (1) automatic differentiation, used in the physics-informed neural networks (PINNs) for scenarios with explicitly known partial differential equations (PDEs), and (2) operator regression using the deep operator network (DeepONet) for PDE-agnostic scenarios. We then test the proposed method for (1) meta-learning for one-dimensional regression, and forward/inverse PDE problems (combined with PINNs); (2) PDE-agnostic physical problems (combined with DeepONet), e.g., fractional diffusion as well as saturated stochastic (100-dimensional) flows in heterogeneous porous media; and (3) spatial-temporal regression problems, i.e., inference of a marine riser displacement field. The results demonstrate that the proposed approach can provide accurate predictions as well as uncertainty quantification given very limited scattered and noisy data, since historical data could be available to provide informative priors. In summary, the proposed method is capable of learning flexible functional priors, and can be extended to big data problems using stochastic HMC or normalizing flows since the latent space is generally characterized as low dimensional.
Multi-fidelity Bayesian Neural Networks: Algorithms and Applications
Dec 19, 2020



Abstract:We propose a new class of Bayesian neural networks (BNNs) that can be trained using noisy data of variable fidelity, and we apply them to learn function approximations as well as to solve inverse problems based on partial differential equations (PDEs). These multi-fidelity BNNs consist of three neural networks: The first is a fully connected neural network, which is trained following the maximum a posteriori probability (MAP) method to fit the low-fidelity data; the second is a Bayesian neural network employed to capture the cross-correlation with uncertainty quantification between the low- and high-fidelity data; and the last one is the physics-informed neural network, which encodes the physical laws described by PDEs. For the training of the last two neural networks, we use the Hamiltonian Monte Carlo method to estimate accurately the posterior distributions for the corresponding hyperparameters. We demonstrate the accuracy of the present method using synthetic data as well as real measurements. Specifically, we first approximate a one- and four-dimensional function, and then infer the reaction rates in one- and two-dimensional diffusion-reaction systems. Moreover, we infer the sea surface temperature (SST) in the Massachusetts and Cape Cod Bays using satellite images and in-situ measurements. Taken together, our results demonstrate that the present method can capture both linear and nonlinear correlation between the low- and high-fideilty data adaptively, identify unknown parameters in PDEs, and quantify uncertainties in predictions, given a few scattered noisy high-fidelity data. Finally, we demonstrate that we can effectively and efficiently reduce the uncertainties and hence enhance the prediction accuracy with an active learning approach, using as examples a specific one-dimensional function approximation and an inverse PDE problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge