A Data-Driven Framework for Discovering Fractional Differential Equations in Complex Systems

In complex physical systems, conventional differential equations often fall short in capturing non-local and memory effects, as they are limited to local dynamics and integer-order interactions. This study introduces a stepwise data-driven framework for discovering fractional differential equations (FDEs) directly from data. FDEs, known for their capacity to model non-local dynamics with fewer parameters than integer-order derivatives, can represent complex systems with long-range interactions. Our framework applies deep neural networks as surrogate models for denoising and reconstructing sparse and noisy observations while using Gaussian-Jacobi quadrature to handle the challenges posed by singularities in fractional derivatives. To optimize both the sparse coefficients and fractional order, we employ an alternating optimization approach that combines sparse regression with global optimization techniques. We validate the framework across various datasets, including synthetic anomalous diffusion data, experimental data on the creep behavior of frozen soils, and single-particle trajectories modeled by L\'{e}vy motion. Results demonstrate the framework's robustness in identifying the structure of FDEs across diverse noise levels and its capacity to capture integer-order dynamics, offering a flexible approach for modeling memory effects in complex systems.

Operator Learning Enhanced Physics-informed Neural Networks for Solving Partial Differential Equations Characterized by Sharp Solutions

Physics-informed Neural Networks (PINNs) have been shown as a promising approach for solving both forward and inverse problems of partial differential equations (PDEs). Meanwhile, the neural operator approach, including methods such as Deep Operator Network (DeepONet) and Fourier neural operator (FNO), has been introduced and extensively employed in approximating solution of PDEs. Nevertheless, to solve problems consisting of sharp solutions poses a significant challenge when employing these two approaches. To address this issue, we propose in this work a novel framework termed Operator Learning Enhanced Physics-informed Neural Networks (OL-PINN). Initially, we utilize DeepONet to learn the solution operator for a set of smooth problems relevant to the PDEs characterized by sharp solutions. Subsequently, we integrate the pre-trained DeepONet with PINN to resolve the target sharp solution problem. We showcase the efficacy of OL-PINN by successfully addressing various problems, such as the nonlinear diffusion-reaction equation, the Burgers equation and the incompressible Navier-Stokes equation at high Reynolds number. Compared with the vanilla PINN, the proposed method requires only a small number of residual points to achieve a strong generalization capability. Moreover, it substantially enhances accuracy, while also ensuring a robust training process. Furthermore, OL-PINN inherits the advantage of PINN for solving inverse problems. To this end, we apply the OL-PINN approach for solving problems with only partial boundary conditions, which usually cannot be solved by the classical numerical methods, showing its capacity in solving ill-posed problems and consequently more complex inverse problems.

Physics-informed neural networks for inverse problems in supersonic flows

Accurate solutions to inverse supersonic compressible flow problems are often required for designing specialized aerospace vehicles. In particular, we consider the problem where we have data available for density gradients from Schlieren photography as well as data at the inflow and part of wall boundaries. These inverse problems are notoriously difficult and traditional methods may not be adequate to solve such ill-posed inverse problems. To this end, we employ the physics-informed neural networks (PINNs) and its extended version, extended PINNs (XPINNs), where domain decomposition allows deploying locally powerful neural networks in each subdomain, which can provide additional expressivity in subdomains, where a complex solution is expected. Apart from the governing compressible Euler equations, we also enforce the entropy conditions in order to obtain viscosity solutions. Moreover, we enforce positivity conditions on density and pressure. We consider inverse problems involving two-dimensional expansion waves, two-dimensional oblique and bow shock waves. We compare solutions obtained by PINNs and XPINNs and invoke some theoretical results that can be used to decide on the generalization errors of the two methods.

Learning Functional Priors and Posteriors from Data and Physics

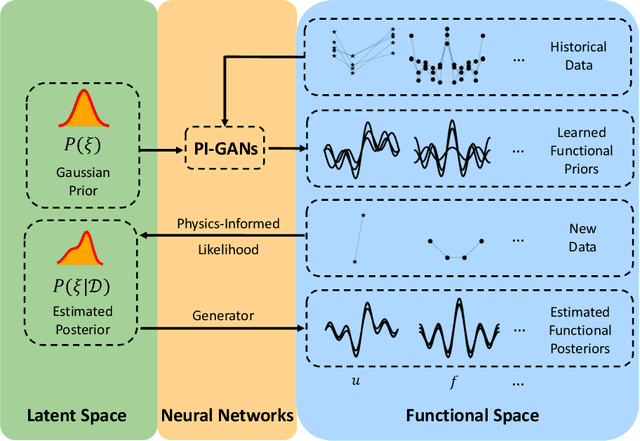
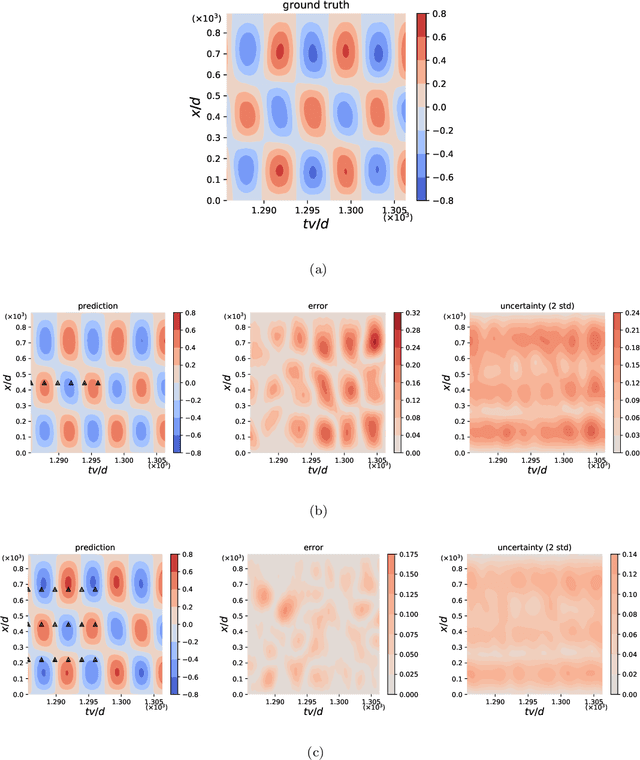
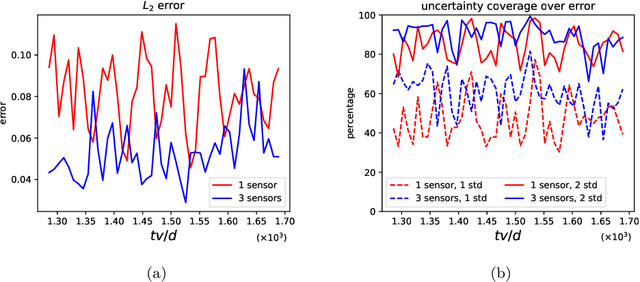
We develop a new Bayesian framework based on deep neural networks to be able to extrapolate in space-time using historical data and to quantify uncertainties arising from both noisy and gappy data in physical problems. Specifically, the proposed approach has two stages: (1) prior learning and (2) posterior estimation. At the first stage, we employ the physics-informed Generative Adversarial Networks (PI-GAN) to learn a functional prior either from a prescribed function distribution, e.g., Gaussian process, or from historical data and physics. At the second stage, we employ the Hamiltonian Monte Carlo (HMC) method to estimate the posterior in the latent space of PI-GANs. In addition, we use two different approaches to encode the physics: (1) automatic differentiation, used in the physics-informed neural networks (PINNs) for scenarios with explicitly known partial differential equations (PDEs), and (2) operator regression using the deep operator network (DeepONet) for PDE-agnostic scenarios. We then test the proposed method for (1) meta-learning for one-dimensional regression, and forward/inverse PDE problems (combined with PINNs); (2) PDE-agnostic physical problems (combined with DeepONet), e.g., fractional diffusion as well as saturated stochastic (100-dimensional) flows in heterogeneous porous media; and (3) spatial-temporal regression problems, i.e., inference of a marine riser displacement field. The results demonstrate that the proposed approach can provide accurate predictions as well as uncertainty quantification given very limited scattered and noisy data, since historical data could be available to provide informative priors. In summary, the proposed method is capable of learning flexible functional priors, and can be extended to big data problems using stochastic HMC or normalizing flows since the latent space is generally characterized as low dimensional.

Physics-informed neural networks (PINNs) for fluid mechanics: A review

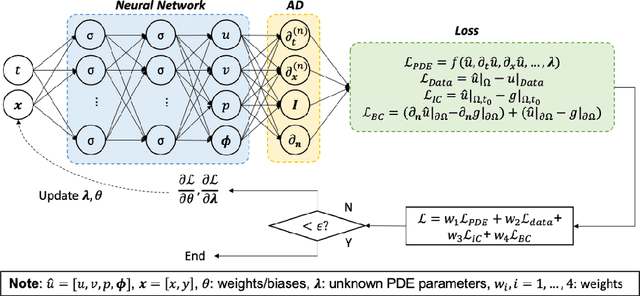
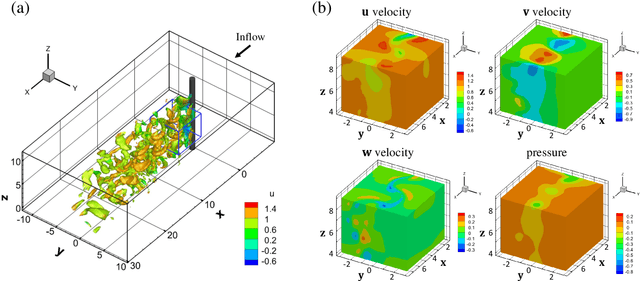
Despite the significant progress over the last 50 years in simulating flow problems using numerical discretization of the Navier-Stokes equations (NSE), we still cannot incorporate seamlessly noisy data into existing algorithms, mesh-generation is complex, and we cannot tackle high-dimensional problems governed by parametrized NSE. Moreover, solving inverse flow problems is often prohibitively expensive and requires complex and expensive formulations and new computer codes. Here, we review flow physics-informed learning, integrating seamlessly data and mathematical models, and implementing them using physics-informed neural networks (PINNs). We demonstrate the effectiveness of PINNs for inverse problems related to three-dimensional wake flows, supersonic flows, and biomedical flows.

DeepXDE: A deep learning library for solving differential equations

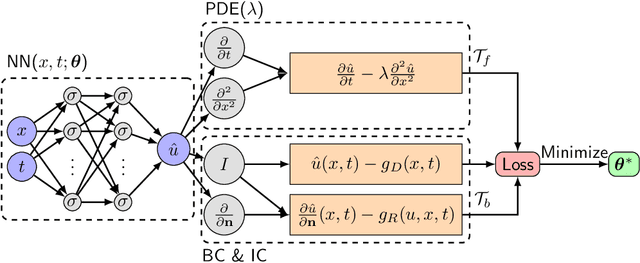
Deep learning has achieved remarkable success in diverse applications; however, its use in solving partial differential equations (PDEs) has emerged only recently. Here, we present an overview of physics-informed neural networks (PINNs), which embed a PDE into the loss of the neural network using automatic differentiation. The PINN algorithm is simple, and it can be applied to different types of PDEs, including integro-differential equations, fractional PDEs, and stochastic PDEs. Moreover, PINNs solve inverse problems as easily as forward problems. We propose a new residual-based adaptive refinement (RAR) method to improve the training efficiency of PINNs. For pedagogical reasons, we compare the PINN algorithm to a standard finite element method. We also present a Python library for PINNs, DeepXDE, which is designed to serve both as an education tool to be used in the classroom as well as a research tool for solving problems in computational science and engineering. DeepXDE supports complex-geometry domains based on the technique of constructive solid geometry, and enables the user code to be compact, resembling closely the mathematical formulation. We introduce the usage of DeepXDE and its customizability, and we also demonstrate the capability of PINNs and the user-friendliness of DeepXDE for five different examples. More broadly, DeepXDE contributes to the more rapid development of the emerging Scientific Machine Learning field.

Nonlocal flocking dynamics: Learning the fractional order of PDEs from particle simulations

Flocking refers to collective behavior of a large number of interacting entities, where the interactions between discrete individuals produce collective motion on the large scale. We employ an agent-based model to describe the microscopic dynamics of each individual in a flock, and use a fractional PDE to model the evolution of macroscopic quantities of interest. The macroscopic models with phenomenological interaction functions are derived by applying the continuum hypothesis to the microscopic model. Instead of specifying the fPDEs with an ad hoc fractional order for nonlocal flocking dynamics, we learn the effective nonlocal influence function in fPDEs directly from particle trajectories generated by the agent-based simulations. We demonstrate how the learning framework is used to connect the discrete agent-based model to the continuum fPDEs in 1D and 2D nonlocal flocking dynamics. In particular, a Cucker-Smale particle model is employed to describe the microscale dynamics of each individual, while Euler equations with nonlocal interaction terms are used to compute the evolution of macroscale quantities. The trajectories generated by the particle simulations mimic the field data of tracking logs that can be obtained experimentally. They can be used to learn the fractional order of the influence function using a Gaussian process regression model implemented with the Bayesian optimization. We show that the numerical solution of the learned Euler equations solved by the finite volume scheme can yield correct density distributions consistent with the collective behavior of the agent-based system. The proposed method offers new insights on how to scale the discrete agent-based models to the continuum-based PDE models, and could serve as a paradigm on extracting effective governing equations for nonlocal flocking dynamics directly from particle trajectories.