Importance of localized dilatation and distensibility in identifying determinants of thoracic aortic aneurysm with neural operators

Thoracic aortic aneurysms (TAAs) arise from diverse mechanical and mechanobiological disruptions to the aortic wall that increase the risk of dissection or rupture. Evidence links TAA development to dysfunctions in the aortic mechanotransduction axis, including loss of elastic fiber integrity and cell-matrix connections. Because distinct insults create different mechanical vulnerabilities, there is a critical need to identify interacting factors that drive progression. Here, we use a finite element framework to generate synthetic TAAs from hundreds of heterogeneous insults spanning varying degrees of elastic fiber damage and impaired mechanosensing. From these simulations, we construct spatial maps of localized dilatation and distensibility to train neural networks that predict the initiating combined insult. We compare several architectures (Deep Operator Networks, UNets, and Laplace Neural Operators) and multiple input data formats to define a standard for future subject-specific modeling. We also quantify predictive performance when networks are trained using only geometric data (dilatation) versus both geometric and mechanical data (dilatation plus distensibility). Across all networks, prediction errors are significantly higher when trained on dilatation alone, underscoring the added value of distensibility information. Among the tested models, UNet consistently provides the highest accuracy across all data formats. These findings highlight the importance of acquiring full-field measurements of both dilatation and distensibility in TAA assessment to reveal the mechanobiological drivers of disease and support the development of personalized treatment strategies.

Equilibrium Conserving Neural Operators for Super-Resolution Learning

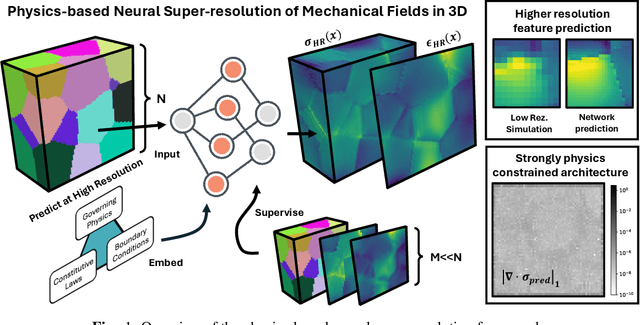
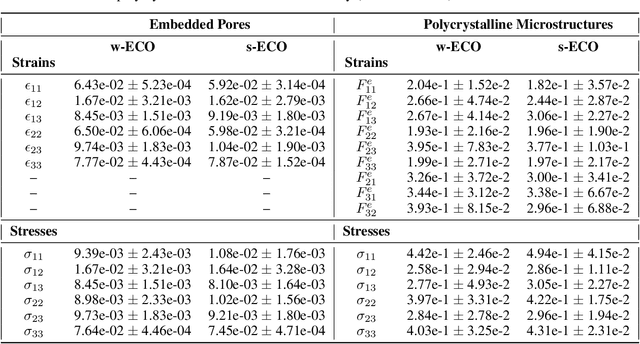
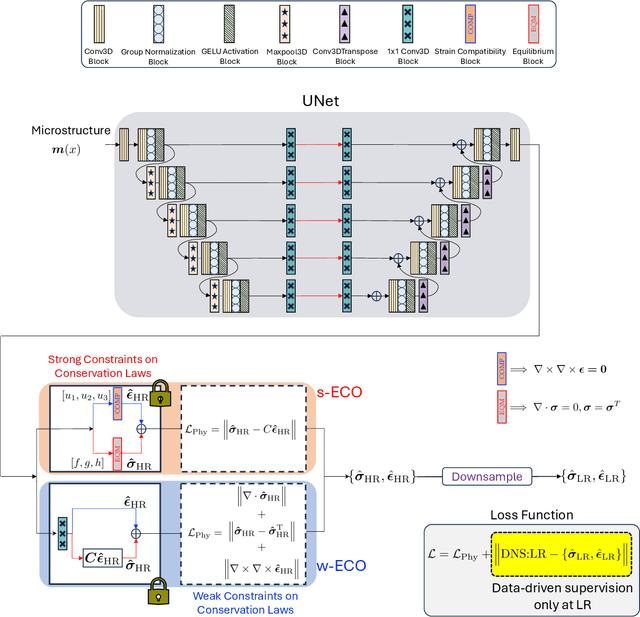
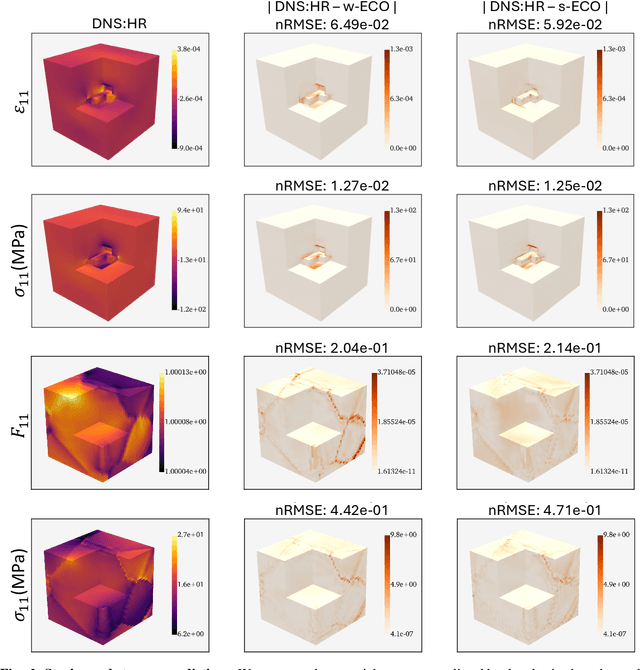
Neural surrogate solvers can estimate solutions to partial differential equations in physical problems more efficiently than standard numerical methods, but require extensive high-resolution training data. In this paper, we break this limitation; we introduce a framework for super-resolution learning in solid mechanics problems. Our approach allows one to train a high-resolution neural network using only low-resolution data. Our Equilibrium Conserving Operator (ECO) architecture embeds known physics directly into the network to make up for missing high-resolution information during training. We evaluate this ECO-based super-resolution framework that strongly enforces conservation-laws in the predicted solutions on two working examples: embedded pores in a homogenized matrix and randomly textured polycrystalline materials. ECO eliminates the reliance on high-fidelity data and reduces the upfront cost of data collection by two orders of magnitude, offering a robust pathway for resource-efficient surrogate modeling in materials modeling. ECO is readily generalizable to other physics-based problems.

Multifidelity Deep Operator Networks

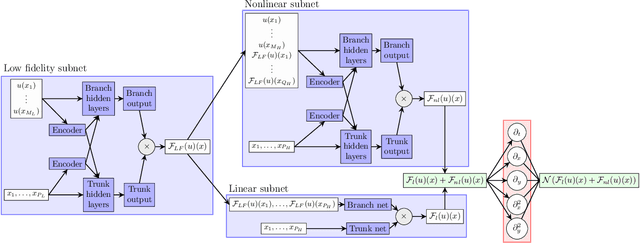
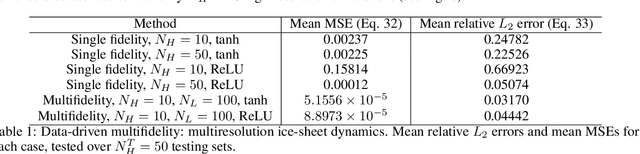
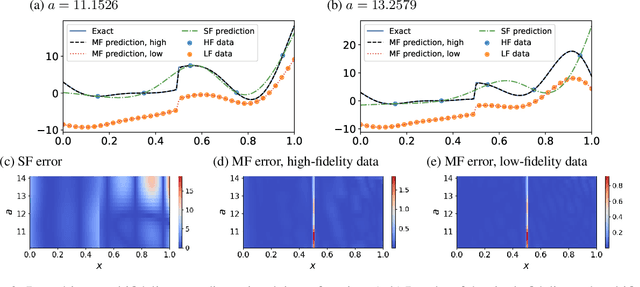
Operator learning for complex nonlinear operators is increasingly common in modeling physical systems. However, training machine learning methods to learn such operators requires a large amount of expensive, high-fidelity data. In this work, we present a composite Deep Operator Network (DeepONet) for learning using two datasets with different levels of fidelity, to accurately learn complex operators when sufficient high-fidelity data is not available. Additionally, we demonstrate that the presence of low-fidelity data can improve the predictions of physics-informed learning with DeepONets.

nPINNs: nonlocal Physics-Informed Neural Networks for a parametrized nonlocal universal Laplacian operator. Algorithms and Applications

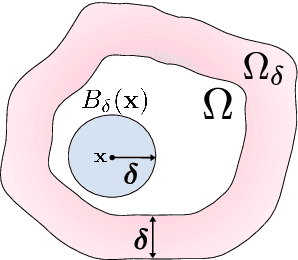
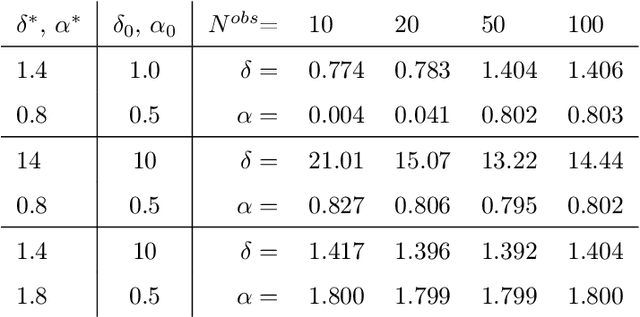
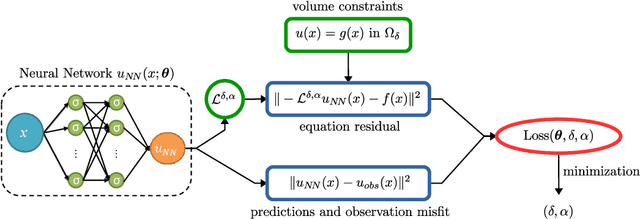
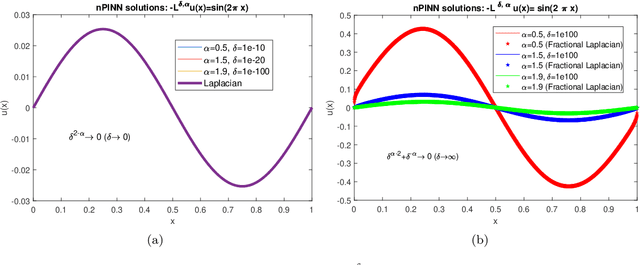
Physics-informed neural networks (PINNs) are effective in solving inverse problems based on differential and integral equations with sparse, noisy, unstructured, and multi-fidelity data. PINNs incorporate all available information into a loss function, thus recasting the original problem into an optimization problem. In this paper, we extend PINNs to parameter and function inference for integral equations such as nonlocal Poisson and nonlocal turbulence models, and we refer to them as nonlocal PINNs (nPINNs). The contribution of the paper is three-fold. First, we propose a unified nonlocal operator, which converges to the classical Laplacian as one of the operator parameters, the nonlocal interaction radius $\delta$ goes to zero, and to the fractional Laplacian as $\delta$ goes to infinity. This universal operator forms a super-set of classical Laplacian and fractional Laplacian operators and, thus, has the potential to fit a broad spectrum of data sets. We provide theoretical convergence rates with respect to $\delta$ and verify them via numerical experiments. Second, we use nPINNs to estimate the two parameters, $\delta$ and $\alpha$. The strong non-convexity of the loss function yielding multiple (good) local minima reveals the occurrence of the operator mimicking phenomenon: different pairs of estimated parameters could produce multiple solutions of comparable accuracy. Third, we propose another nonlocal operator with spatially variable order $\alpha(y)$, which is more suitable for modeling turbulent Couette flow. Our results show that nPINNs can jointly infer this function as well as $\delta$. Also, these parameters exhibit a universal behavior with respect to the Reynolds number, a finding that contributes to our understanding of nonlocal interactions in wall-bounded turbulence.

DeepXDE: A deep learning library for solving differential equations

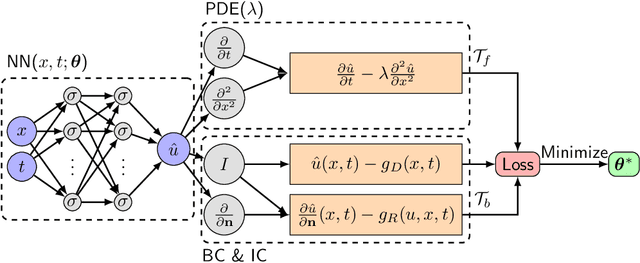
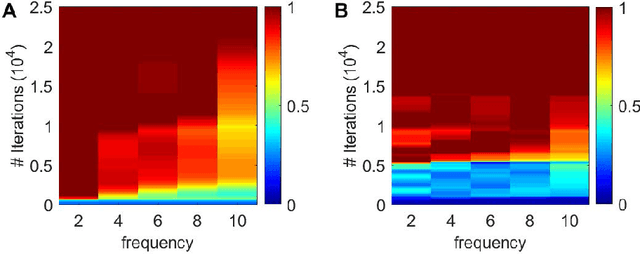
Deep learning has achieved remarkable success in diverse applications; however, its use in solving partial differential equations (PDEs) has emerged only recently. Here, we present an overview of physics-informed neural networks (PINNs), which embed a PDE into the loss of the neural network using automatic differentiation. The PINN algorithm is simple, and it can be applied to different types of PDEs, including integro-differential equations, fractional PDEs, and stochastic PDEs. Moreover, PINNs solve inverse problems as easily as forward problems. We propose a new residual-based adaptive refinement (RAR) method to improve the training efficiency of PINNs. For pedagogical reasons, we compare the PINN algorithm to a standard finite element method. We also present a Python library for PINNs, DeepXDE, which is designed to serve both as an education tool to be used in the classroom as well as a research tool for solving problems in computational science and engineering. DeepXDE supports complex-geometry domains based on the technique of constructive solid geometry, and enables the user code to be compact, resembling closely the mathematical formulation. We introduce the usage of DeepXDE and its customizability, and we also demonstrate the capability of PINNs and the user-friendliness of DeepXDE for five different examples. More broadly, DeepXDE contributes to the more rapid development of the emerging Scientific Machine Learning field.

Linking Gaussian Process regression with data-driven manifold embeddings for nonlinear data fusion

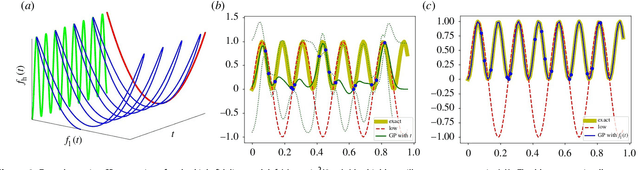
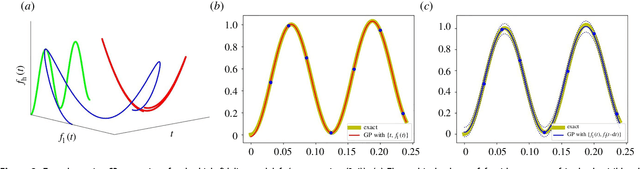
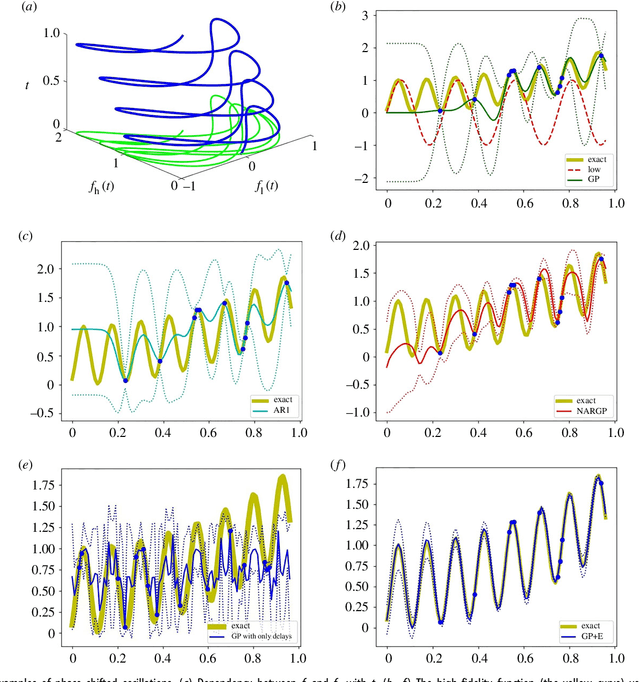
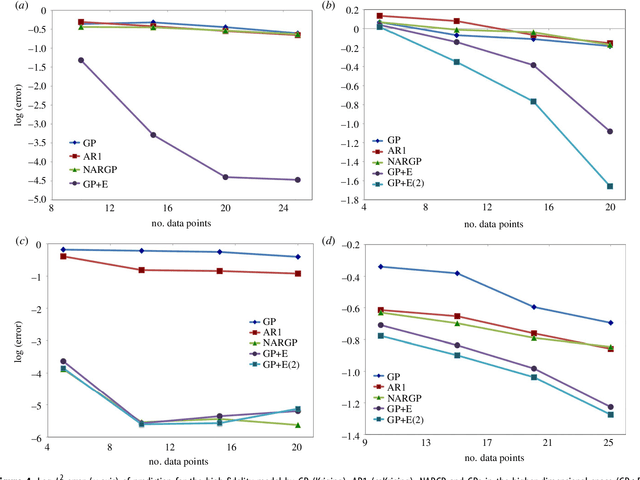
In statistical modeling with Gaussian Process regression, it has been shown that combining (few) high-fidelity data with (many) low-fidelity data can enhance prediction accuracy, compared to prediction based on the few high-fidelity data only. Such information fusion techniques for multifidelity data commonly approach the high-fidelity model $f_h(t)$ as a function of two variables $(t,y)$, and then using $f_l(t)$ as the $y$ data. More generally, the high-fidelity model can be written as a function of several variables $(t,y_1,y_2....)$; the low-fidelity model $f_l$ and, say, some of its derivatives, can then be substituted for these variables. In this paper, we will explore mathematical algorithms for multifidelity information fusion that use such an approach towards improving the representation of the high-fidelity function with only a few training data points. Given that $f_h$ may not be a simple function -- and sometimes not even a function -- of $f_l$, we demonstrate that using additional functions of $t$, such as derivatives or shifts of $f_l$, can drastically improve the approximation of $f_h$ through Gaussian Processes. We also point out a connection with "embedology" techniques from topology and dynamical systems.