Panos Stinis
From LIF to QIF: Toward Differentiable Spiking Neurons for Scientific Machine Learning
Nov 10, 2025Abstract:Spiking neural networks (SNNs) offer biologically inspired computation but remain underexplored for continuous regression tasks in scientific machine learning. In this work, we introduce and systematically evaluate Quadratic Integrate-and-Fire (QIF) neurons as an alternative to the conventional Leaky Integrate-and-Fire (LIF) model in both directly trained SNNs and ANN-to-SNN conversion frameworks. The QIF neuron exhibits smooth and differentiable spiking dynamics, enabling gradient-based training and stable optimization within architectures such as multilayer perceptrons (MLPs), Deep Operator Networks (DeepONets), and Physics-Informed Neural Networks (PINNs). Across benchmarks on function approximation, operator learning, and partial differential equation (PDE) solving, QIF-based networks yield smoother, more accurate, and more stable predictions than their LIF counterparts, which suffer from discontinuous time-step responses and jagged activation surfaces. These results position the QIF neuron as a computational bridge between spiking and continuous-valued deep learning, advancing the integration of neuroscience-inspired dynamics into physics-informed and operator-learning frameworks.
Self-adaptive weighting and sampling for physics-informed neural networks
Nov 07, 2025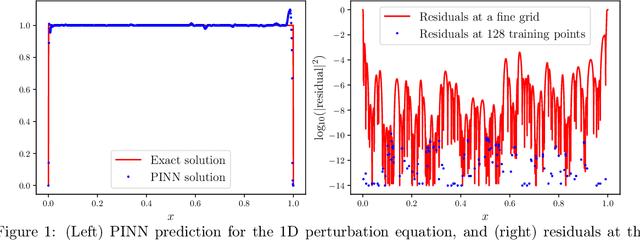
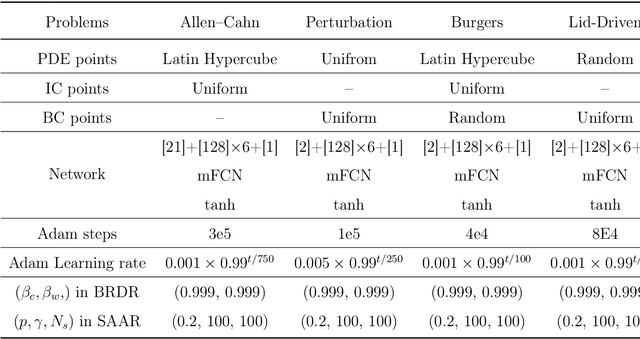
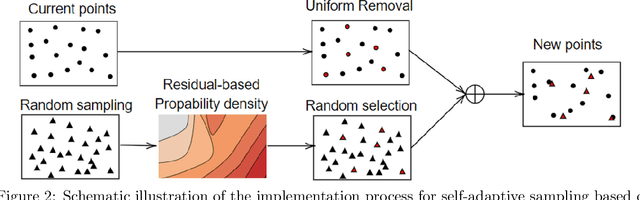
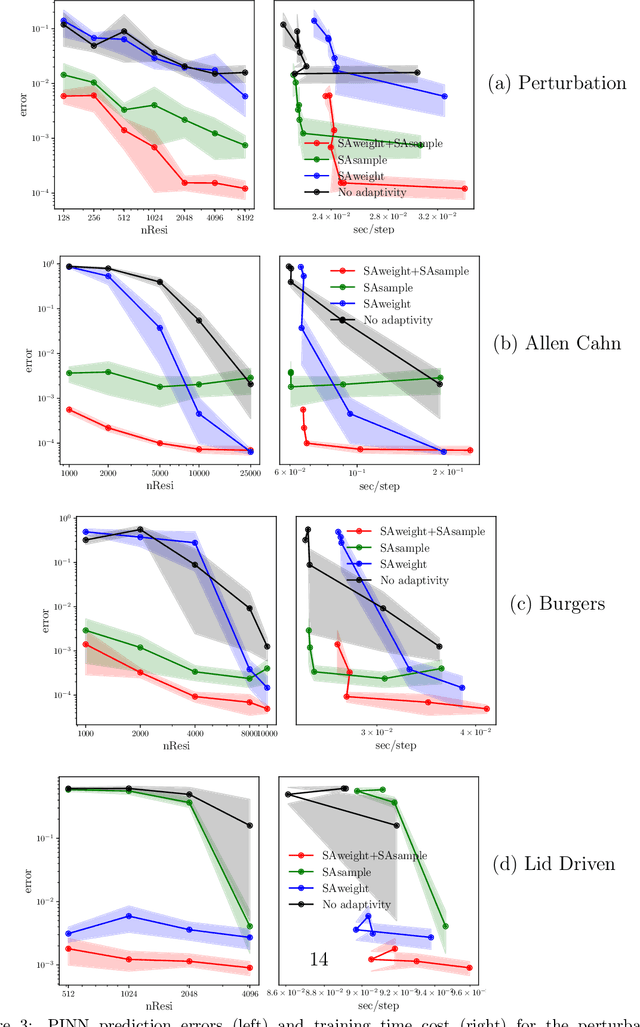
Abstract:Physics-informed deep learning has emerged as a promising framework for solving partial differential equations (PDEs). Nevertheless, training these models on complex problems remains challenging, often leading to limited accuracy and efficiency. In this work, we introduce a hybrid adaptive sampling and weighting method to enhance the performance of physics-informed neural networks (PINNs). The adaptive sampling component identifies training points in regions where the solution exhibits rapid variation, while the adaptive weighting component balances the convergence rate across training points. Numerical experiments show that applying only adaptive sampling or only adaptive weighting is insufficient to consistently achieve accurate predictions, particularly when training points are scarce. Since each method emphasizes different aspects of the solution, their effectiveness is problem dependent. By combining both strategies, the proposed framework consistently improves prediction accuracy and training efficiency, offering a more robust approach for solving PDEs with PINNs.
Physics-Informed DeepONet Coupled with FEM for Convective Transport in Porous Media with Sharp Gaussian Sources
Aug 27, 2025Abstract:We present a hybrid framework that couples finite element methods (FEM) with physics-informed DeepONet to model fluid transport in porous media from sharp, localized Gaussian sources. The governing system consists of a steady-state Darcy flow equation and a time-dependent convection-diffusion equation. Our approach solves the Darcy system using FEM and transfers the resulting velocity field to a physics-informed DeepONet, which learns the mapping from source functions to solute concentration profiles. This modular strategy preserves FEM-level accuracy in the flow field while enabling fast inference for transport dynamics. To handle steep gradients induced by sharp sources, we introduce an adaptive sampling strategy for trunk collocation points. Numerical experiments demonstrate that our method is in good agreement with the reference solutions while offering orders of magnitude speedups over traditional solvers, making it suitable for practical applications in relevant scenarios. Implementation of our proposed method is available at https://github.com/erkara/fem-pi-deeponet.
Stabilizing PDE--ML Coupled System
Jun 24, 2025Abstract:A long-standing obstacle in the use of machine-learnt surrogates with larger PDE systems is the onset of instabilities when solved numerically. Efforts towards ameliorating these have mostly concentrated on improving the accuracy of the surrogates or imbuing them with additional structure, and have garnered limited success. In this article, we study a prototype problem and draw insights that can help with more complex systems. In particular, we focus on a viscous Burgers'-ML system and, after identifying the cause of the instabilities, prescribe strategies to stabilize the coupled system. To improve the accuracy of the stabilized system, we next explore methods based on the Mori--Zwanzig formalism.
Conformalized-KANs: Uncertainty Quantification with Coverage Guarantees for Kolmogorov-Arnold Networks (KANs) in Scientific Machine Learning
Apr 21, 2025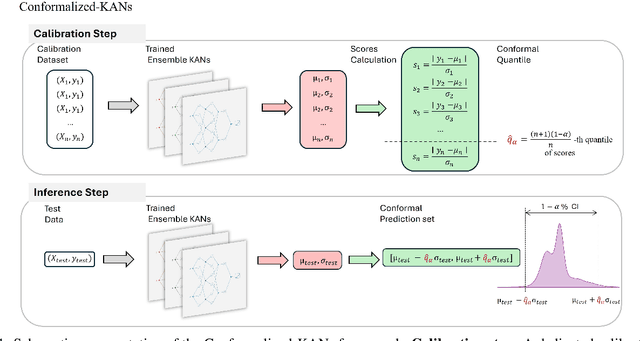

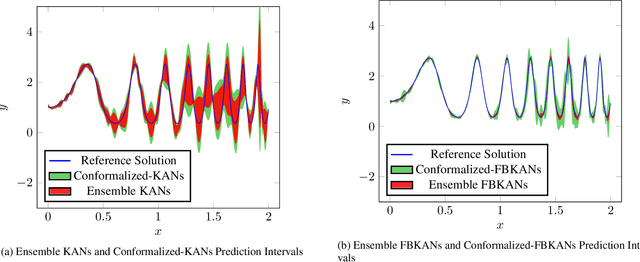

Abstract:This paper explores uncertainty quantification (UQ) methods in the context of Kolmogorov-Arnold Networks (KANs). We apply an ensemble approach to KANs to obtain a heuristic measure of UQ, enhancing interpretability and robustness in modeling complex functions. Building on this, we introduce Conformalized-KANs, which integrate conformal prediction, a distribution-free UQ technique, with KAN ensembles to generate calibrated prediction intervals with guaranteed coverage. Extensive numerical experiments are conducted to evaluate the effectiveness of these methods, focusing particularly on the robustness and accuracy of the prediction intervals under various hyperparameter settings. We show that the conformal KAN predictions can be applied to recent extensions of KANs, including Finite Basis KANs (FBKANs) and multifideilty KANs (MFKANs). The results demonstrate the potential of our approaches to improve the reliability and applicability of KANs in scientific machine learning.
E-PINNs: Epistemic Physics-Informed Neural Networks
Mar 25, 2025



Abstract:Physics-informed neural networks (PINNs) have demonstrated promise as a framework for solving forward and inverse problems involving partial differential equations. Despite recent progress in the field, it remains challenging to quantify uncertainty in these networks. While approaches such as Bayesian PINNs (B-PINNs) provide a principled approach to capturing uncertainty through Bayesian inference, they can be computationally expensive for large-scale applications. In this work, we propose Epistemic Physics-Informed Neural Networks (E-PINNs), a framework that leverages a small network, the \emph{epinet}, to efficiently quantify uncertainty in PINNs. The proposed approach works as an add-on to existing, pre-trained PINNs with a small computational overhead. We demonstrate the applicability of the proposed framework in various test cases and compare the results with B-PINNs using Hamiltonian Monte Carlo (HMC) posterior estimation and dropout-equipped PINNs (Dropout-PINNs). Our experiments show that E-PINNs provide similar coverage to B-PINNs, with often comparable sharpness, while being computationally more efficient. This observation, combined with E-PINNs' more consistent uncertainty estimates and better calibration compared to Dropout-PINNs for the examples presented, indicates that E-PINNs offer a promising approach in terms of accuracy-efficiency trade-off.
What do physics-informed DeepONets learn? Understanding and improving training for scientific computing applications
Nov 27, 2024Abstract:Physics-informed deep operator networks (DeepONets) have emerged as a promising approach toward numerically approximating the solution of partial differential equations (PDEs). In this work, we aim to develop further understanding of what is being learned by physics-informed DeepONets by assessing the universality of the extracted basis functions and demonstrating their potential toward model reduction with spectral methods. Results provide clarity about measuring the performance of a physics-informed DeepONet through the decays of singular values and expansion coefficients. In addition, we propose a transfer learning approach for improving training for physics-informed DeepONets between parameters of the same PDE as well as across different, but related, PDEs where these models struggle to train well. This approach results in significant error reduction and learned basis functions that are more effective in representing the solution of a PDE.
SPIKANs: Separable Physics-Informed Kolmogorov-Arnold Networks
Nov 09, 2024Abstract:Physics-Informed Neural Networks (PINNs) have emerged as a promising method for solving partial differential equations (PDEs) in scientific computing. While PINNs typically use multilayer perceptrons (MLPs) as their underlying architecture, recent advancements have explored alternative neural network structures. One such innovation is the Kolmogorov-Arnold Network (KAN), which has demonstrated benefits over traditional MLPs, including faster neural scaling and better interpretability. The application of KANs to physics-informed learning has led to the development of Physics-Informed KANs (PIKANs), enabling the use of KANs to solve PDEs. However, despite their advantages, KANs often suffer from slower training speeds, particularly in higher-dimensional problems where the number of collocation points grows exponentially with the dimensionality of the system. To address this challenge, we introduce Separable Physics-Informed Kolmogorov-Arnold Networks (SPIKANs). This novel architecture applies the principle of separation of variables to PIKANs, decomposing the problem such that each dimension is handled by an individual KAN. This approach drastically reduces the computational complexity of training without sacrificing accuracy, facilitating their application to higher-dimensional PDEs. Through a series of benchmark problems, we demonstrate the effectiveness of SPIKANs, showcasing their superior scalability and performance compared to PIKANs and highlighting their potential for solving complex, high-dimensional PDEs in scientific computing.
Multifidelity Kolmogorov-Arnold Networks
Oct 18, 2024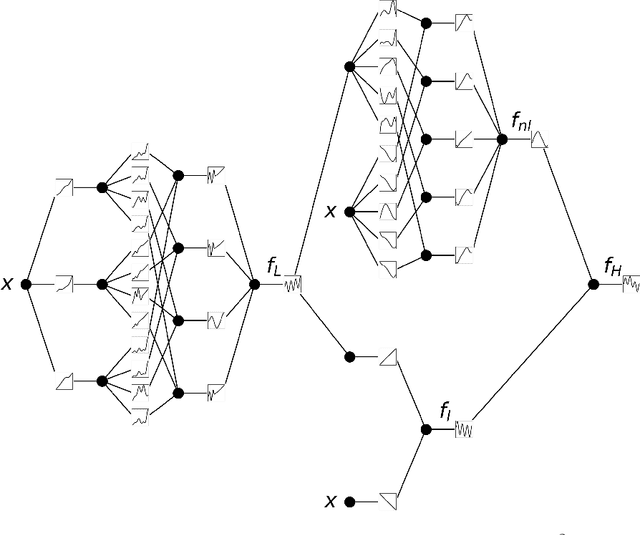



Abstract:We develop a method for multifidelity Kolmogorov-Arnold networks (KANs), which use a low-fidelity model along with a small amount of high-fidelity data to train a model for the high-fidelity data accurately. Multifidelity KANs (MFKANs) reduce the amount of expensive high-fidelity data needed to accurately train a KAN by exploiting the correlations between the low- and high-fidelity data to give accurate and robust predictions in the absence of a large high-fidelity dataset. In addition, we show that multifidelity KANs can be used to increase the accuracy of physics-informed KANs (PIKANs), without the use of training data.
Self-adaptive weights based on balanced residual decay rate for physics-informed neural networks and deep operator networks
Jun 28, 2024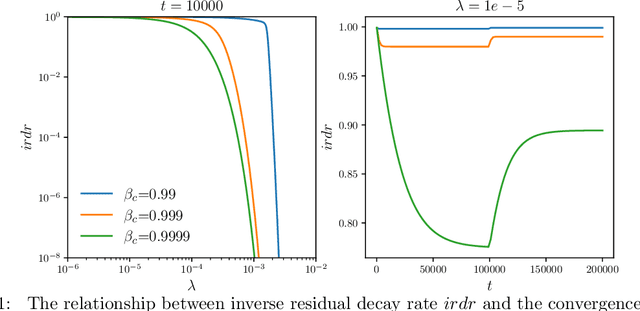

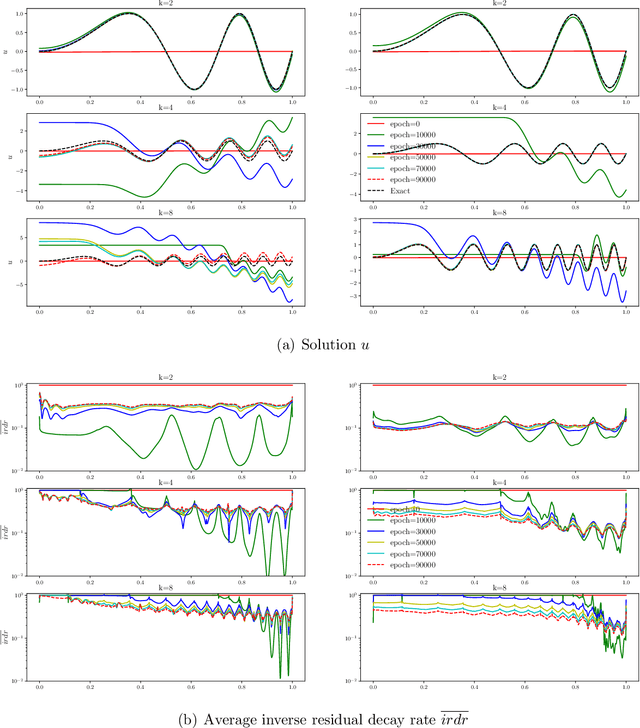
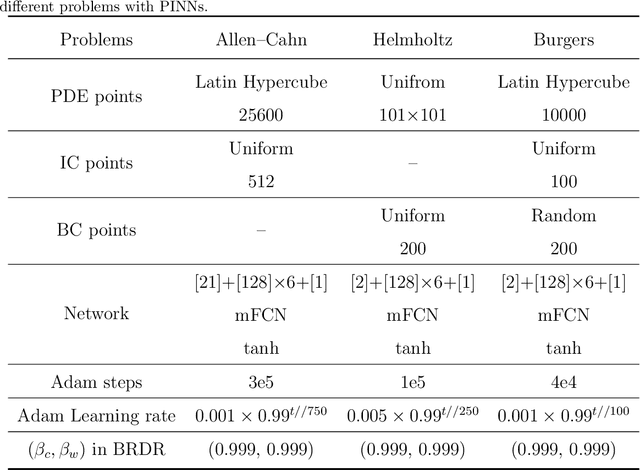
Abstract:Physics-informed deep learning has emerged as a promising alternative for solving partial differential equations. However, for complex problems, training these networks can still be challenging, often resulting in unsatisfactory accuracy and efficiency. In this work, we demonstrate that the failure of plain physics-informed neural networks arises from the significant discrepancy in the convergence speed of residuals at different training points, where the slowest convergence speed dominates the overall solution convergence. Based on these observations, we propose a point-wise adaptive weighting method that balances the residual decay rate across different training points. The performance of our proposed adaptive weighting method is compared with current state-of-the-art adaptive weighting methods on benchmark problems for both physics-informed neural networks and physics-informed deep operator networks. Through extensive numerical results we demonstrate that our proposed approach of balanced residual decay rates offers several advantages, including bounded weights, high prediction accuracy, fast convergence speed, low training uncertainty, low computational cost and ease of hyperparameter tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge