Large scale scattering using fast solvers based on neural operators

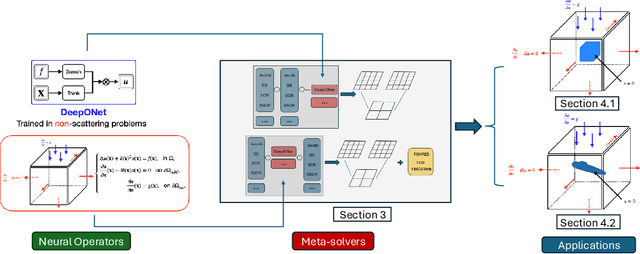
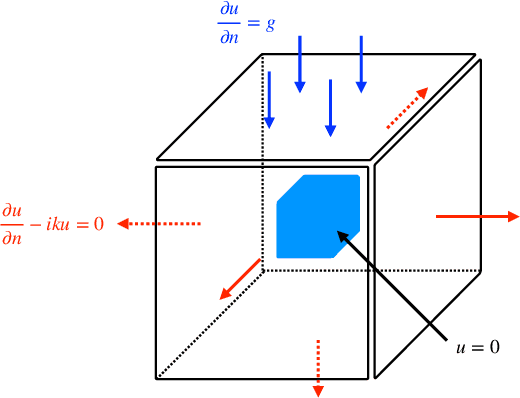
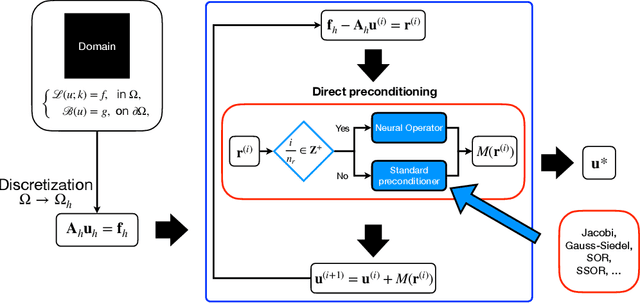
We extend a recently proposed machine-learning-based iterative solver, i.e. the hybrid iterative transferable solver (HINTS), to solve the scattering problem described by the Helmholtz equation in an exterior domain with a complex absorbing boundary condition. The HINTS method combines neural operators (NOs) with standard iterative solvers, e.g. Jacobi and Gauss-Seidel (GS), to achieve better performance by leveraging the spectral bias of neural networks. In HINTS, some iterations of the conventional iterative method are replaced by inferences of the pre-trained NO. In this work, we employ HINTS to solve the scattering problem for both 2D and 3D problems, where the standard iterative solver fails. We consider square and triangular scatterers of various sizes in 2D, and a cube and a model submarine in 3D. We explore and illustrate the extrapolation capability of HINTS in handling diverse geometries of the scatterer, which is achieved by training the NO on non-scattering scenarios and then deploying it in HINTS to solve scattering problems. The accurate results demonstrate that the NO in HINTS method remains effective without retraining or fine-tuning it whenever a new scatterer is given. Taken together, our results highlight the adaptability and versatility of the extended HINTS methodology in addressing diverse scattering problems.

Evaluation Methodology for Large Language Models for Multilingual Document Question and Answer

With the widespread adoption of Large Language Models (LLMs), in this paper we investigate the multilingual capability of these models. Our preliminary results show that, translating the native language context, question and answer into a high resource language produced the best results.

Rethinking Skip Connections in Spiking Neural Networks with Time-To-First-Spike Coding

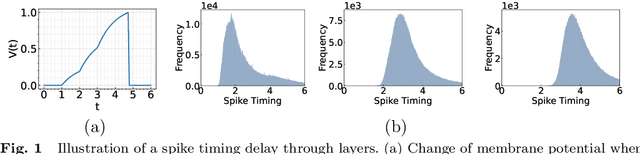
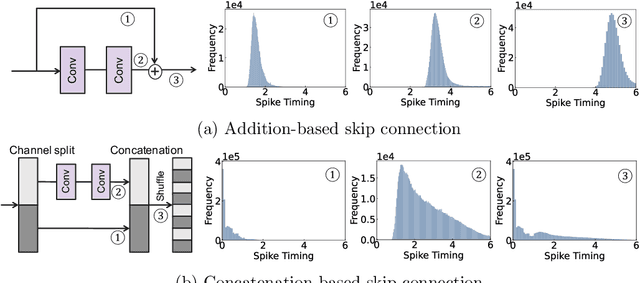
Time-To-First-Spike (TTFS) coding in Spiking Neural Networks (SNNs) offers significant advantages in terms of energy efficiency, closely mimicking the behavior of biological neurons. In this work, we delve into the role of skip connections, a widely used concept in Artificial Neural Networks (ANNs), within the domain of SNNs with TTFS coding. Our focus is on two distinct types of skip connection architectures: (1) addition-based skip connections, and (2) concatenation-based skip connections. We find that addition-based skip connections introduce an additional delay in terms of spike timing. On the other hand, concatenation-based skip connections circumvent this delay but produce time gaps between after-convolution and skip connection paths, thereby restricting the effective mixing of information from these two paths. To mitigate these issues, we propose a novel approach involving a learnable delay for skip connections in the concatenation-based skip connection architecture. This approach successfully bridges the time gap between the convolutional and skip branches, facilitating improved information mixing. We conduct experiments on public datasets including MNIST and Fashion-MNIST, illustrating the advantage of the skip connection in TTFS coding architectures. Additionally, we demonstrate the applicability of TTFS coding on beyond image recognition tasks and extend it to scientific machine-learning tasks, broadening the potential uses of SNNs.

Artificial to Spiking Neural Networks Conversion for Scientific Machine Learning

We introduce a method to convert Physics-Informed Neural Networks (PINNs), commonly used in scientific machine learning, to Spiking Neural Networks (SNNs), which are expected to have higher energy efficiency compared to traditional Artificial Neural Networks (ANNs). We first extend the calibration technique of SNNs to arbitrary activation functions beyond ReLU, making it more versatile, and we prove a theorem that ensures the effectiveness of the calibration. We successfully convert PINNs to SNNs, enabling computational efficiency for diverse regression tasks in solving multiple differential equations, including the unsteady Navier-Stokes equations. We demonstrate great gains in terms of overall efficiency, including Separable PINNs (SPINNs), which accelerate the training process. Overall, this is the first work of this kind and the proposed method achieves relatively good accuracy with low spike rates.

DiTTO: Diffusion-inspired Temporal Transformer Operator

Solving partial differential equations (PDEs) using a data-driven approach has become increasingly common. The recent development of the operator learning paradigm has enabled the solution of a broader range of PDE-related problems. We propose an operator learning method to solve time-dependent PDEs continuously in time without needing any temporal discretization. The proposed approach, named DiTTO, is inspired by latent diffusion models. While diffusion models are usually used in generative artificial intelligence tasks, their time-conditioning mechanism is extremely useful for PDEs. The diffusion-inspired framework is combined with elements from the Transformer architecture to improve its capabilities. We demonstrate the effectiveness of the new approach on a wide variety of PDEs in multiple dimensions, namely the 1-D Burgers' equation, 2-D Navier-Stokes equations, and the acoustic wave equation in 2-D and 3-D. DiTTO achieves state-of-the-art results in terms of accuracy for these problems. We also present a method to improve the performance of DiTTO by using fast sampling concepts from diffusion models. Finally, we show that DiTTO can accurately perform zero-shot super-resolution in time.

Understanding the Efficacy of U-Net & Vision Transformer for Groundwater Numerical Modelling

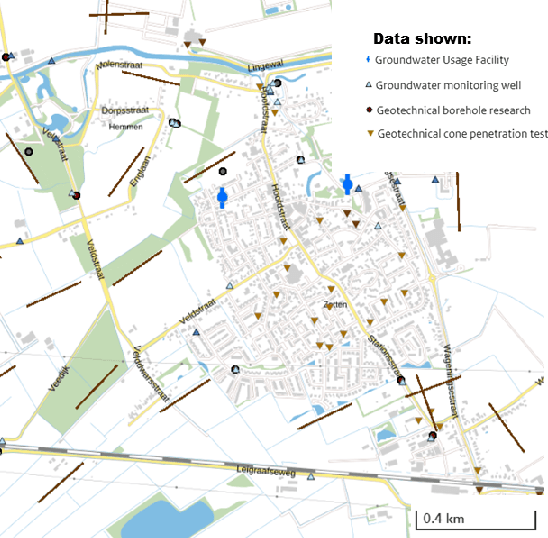
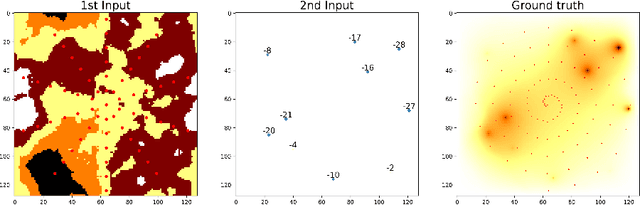
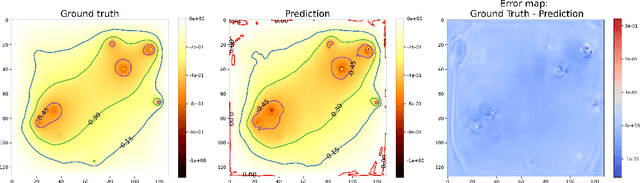
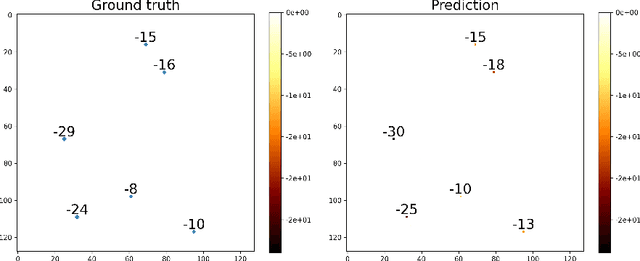
This paper presents a comprehensive comparison of various machine learning models, namely U-Net, U-Net integrated with Vision Transformers (ViT), and Fourier Neural Operator (FNO), for time-dependent forward modelling in groundwater systems. Through testing on synthetic datasets, it is demonstrated that U-Net and U-Net + ViT models outperform FNO in accuracy and efficiency, especially in sparse data scenarios. These findings underscore the potential of U-Net-based models for groundwater modelling in real-world applications where data scarcity is prevalent.

CrunchGPT: A chatGPT assisted framework for scientific machine learning

Scientific Machine Learning (SciML) has advanced recently across many different areas in computational science and engineering. The objective is to integrate data and physics seamlessly without the need of employing elaborate and computationally taxing data assimilation schemes. However, preprocessing, problem formulation, code generation, postprocessing and analysis are still time consuming and may prevent SciML from wide applicability in industrial applications and in digital twin frameworks. Here, we integrate the various stages of SciML under the umbrella of ChatGPT, to formulate CrunchGPT, which plays the role of a conductor orchestrating the entire workflow of SciML based on simple prompts by the user. Specifically, we present two examples that demonstrate the potential use of CrunchGPT in optimizing airfoils in aerodynamics, and in obtaining flow fields in various geometries in interactive mode, with emphasis on the validation stage. To demonstrate the flow of the CrunchGPT, and create an infrastructure that can facilitate a broader vision, we built a webapp based guided user interface, that includes options for a comprehensive summary report. The overall objective is to extend CrunchGPT to handle diverse problems in computational mechanics, design, optimization and controls, and general scientific computing tasks involved in SciML, hence using it as a research assistant tool but also as an educational tool. While here the examples focus in fluid mechanics, future versions will target solid mechanics and materials science, geophysics, systems biology and bioinformatics.

ViTO: Vision Transformer-Operator

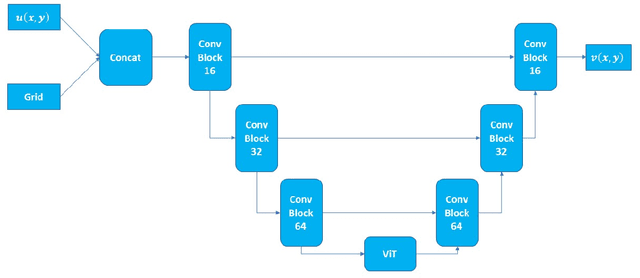
We combine vision transformers with operator learning to solve diverse inverse problems described by partial differential equations (PDEs). Our approach, named ViTO, combines a U-Net based architecture with a vision transformer. We apply ViTO to solve inverse PDE problems of increasing complexity, namely for the wave equation, the Navier-Stokes equations and the Darcy equation. We focus on the more challenging case of super-resolution, where the input dataset for the inverse problem is at a significantly coarser resolution than the output. The results we obtain are comparable or exceed the leading operator network benchmarks in terms of accuracy. Furthermore, ViTO`s architecture has a small number of trainable parameters (less than 10% of the leading competitor), resulting in a performance speed-up of over 5x when averaged over the various test cases.

MessageNet: Message Classification using Natural Language Processing and Meta-data

In this paper we propose a new Deep Learning (DL) approach for message classification. Our method is based on the state-of-the-art Natural Language Processing (NLP) building blocks, combined with a novel technique for infusing the meta-data input that is typically available in messages such as the sender information, timestamps, attached image, audio, affiliations, and more. As we demonstrate throughout the paper, going beyond the mere text by leveraging all available channels in the message, could yield an improved representation and higher classification accuracy. To achieve message representation, each type of input is processed in a dedicated block in the neural network architecture that is suitable for the data type. Such an implementation enables training all blocks together simultaneously, and forming cross channels features in the network. We show in the Experiments Section that in some cases, message's meta-data holds an additional information that cannot be extracted just from the text, and when using this information we achieve better performance. Furthermore, we demonstrate that our multi-modality block approach outperforms other approaches for injecting the meta data to the the text classifier.

SMS: Spiking Marching Scheme for Efficient Long Time Integration of Differential Equations

We propose a Spiking Neural Network (SNN)-based explicit numerical scheme for long time integration of time-dependent Ordinary and Partial Differential Equations (ODEs, PDEs). The core element of the method is a SNN, trained to use spike-encoded information about the solution at previous timesteps to predict spike-encoded information at the next timestep. After the network has been trained, it operates as an explicit numerical scheme that can be used to compute the solution at future timesteps, given a spike-encoded initial condition. A decoder is used to transform the evolved spiking-encoded solution back to function values. We present results from numerical experiments of using the proposed method for ODEs and PDEs of varying complexity.