Generative modeling of Sparse Approximate Inverse Preconditioners

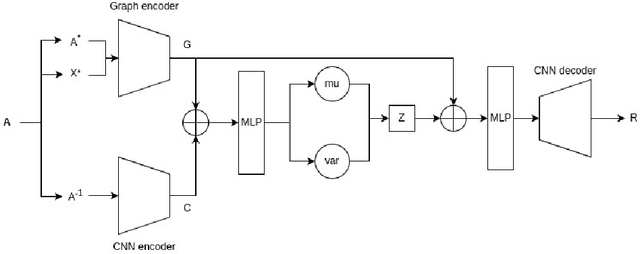
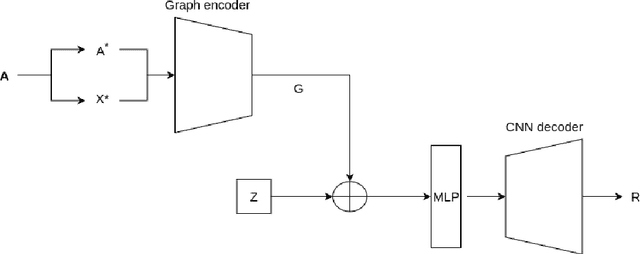
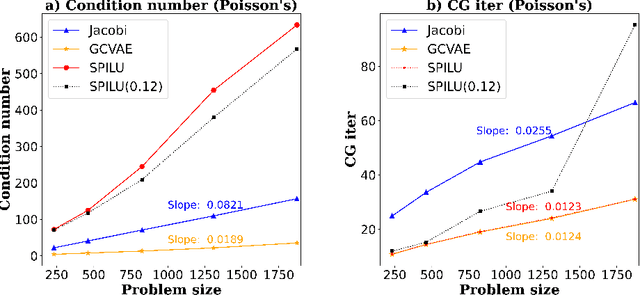
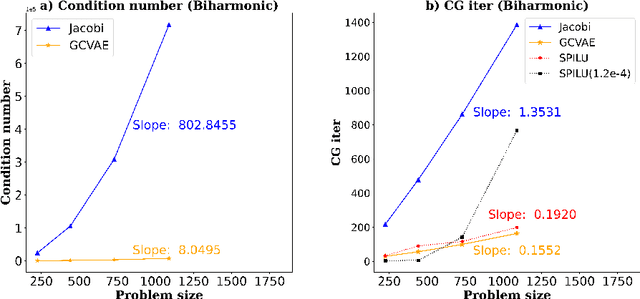
We present a new deep learning paradigm for the generation of sparse approximate inverse (SPAI) preconditioners for matrix systems arising from the mesh-based discretization of elliptic differential operators. Our approach is based upon the observation that matrices generated in this manner are not arbitrary, but inherit properties from differential operators that they discretize. Consequently, we seek to represent a learnable distribution of high-performance preconditioners from a low-dimensional subspace through a carefully-designed autoencoder, which is able to generate SPAI preconditioners for these systems. The concept has been implemented on a variety of finite element discretizations of second- and fourth-order elliptic partial differential equations with highly promising results.

Investigating Guiding Information for Adaptive Collocation Point Sampling in PINNs

Physics-informed neural networks (PINNs) provide a means of obtaining approximate solutions of partial differential equations and systems through the minimisation of an objective function which includes the evaluation of a residual function at a set of collocation points within the domain. The quality of a PINNs solution depends upon numerous parameters, including the number and distribution of these collocation points. In this paper we consider a number of strategies for selecting these points and investigate their impact on the overall accuracy of the method. In particular, we suggest that no single approach is likely to be ``optimal'' but we show how a number of important metrics can have an impact in improving the quality of the results obtained when using a fixed number of residual evaluations. We illustrate these approaches through the use of two benchmark test problems: Burgers' equation and the Allen-Cahn equation.

Understanding the Efficacy of U-Net & Vision Transformer for Groundwater Numerical Modelling

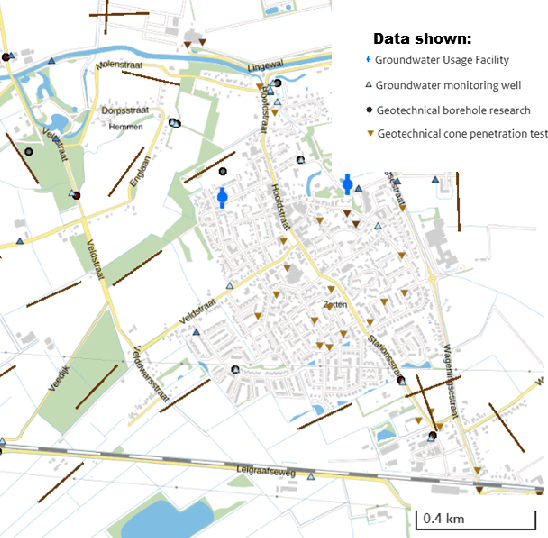
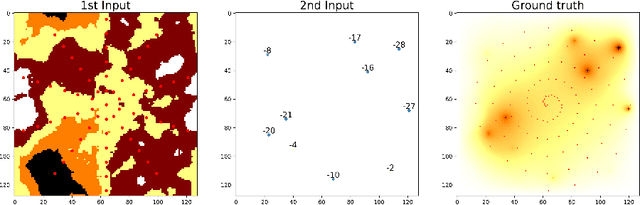
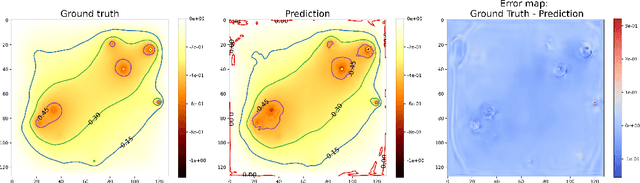
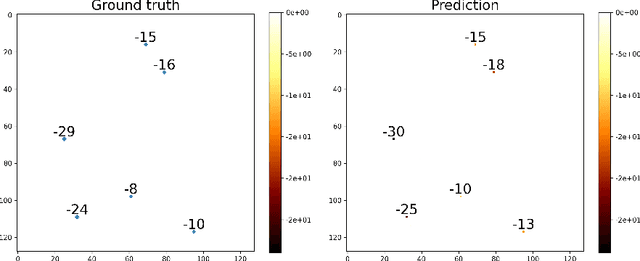
This paper presents a comprehensive comparison of various machine learning models, namely U-Net, U-Net integrated with Vision Transformers (ViT), and Fourier Neural Operator (FNO), for time-dependent forward modelling in groundwater systems. Through testing on synthetic datasets, it is demonstrated that U-Net and U-Net + ViT models outperform FNO in accuracy and efficiency, especially in sparse data scenarios. These findings underscore the potential of U-Net-based models for groundwater modelling in real-world applications where data scarcity is prevalent.

Attention U-Net as a surrogate model for groundwater prediction

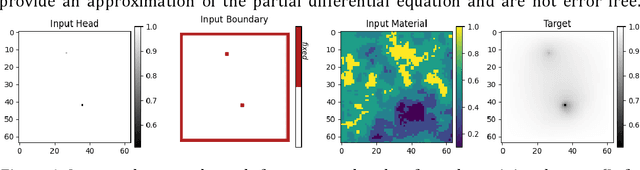
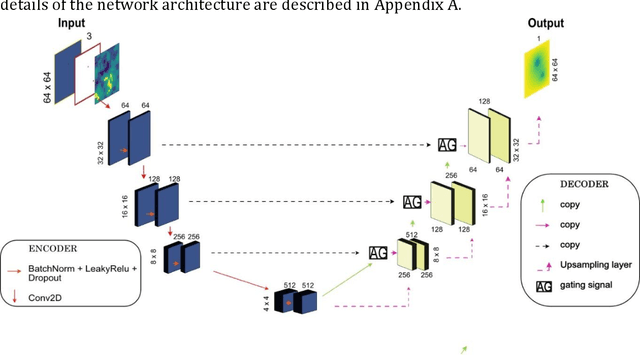
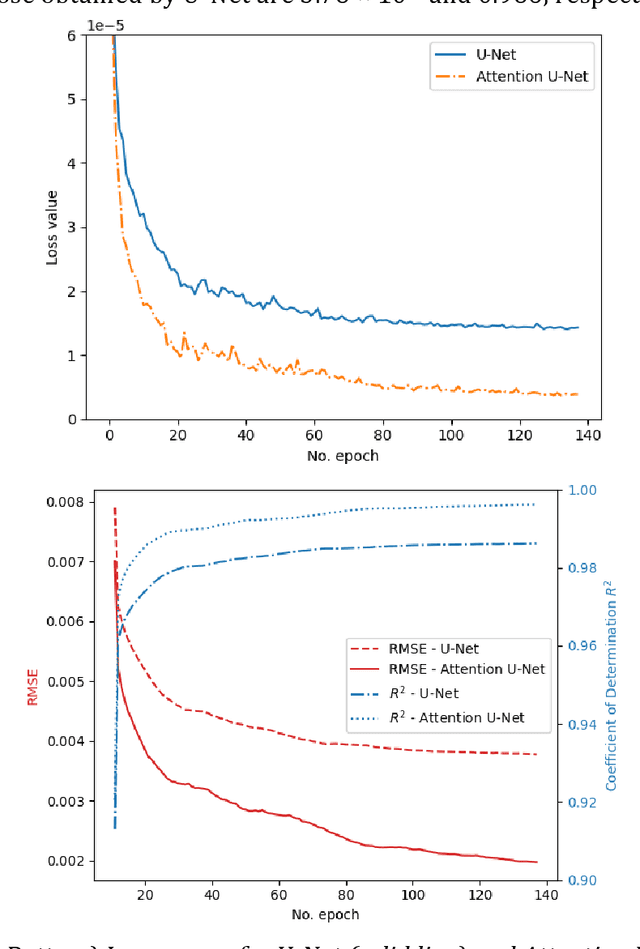
Numerical simulations of groundwater flow are used to analyze and predict the response of an aquifer system to its change in state by approximating the solution of the fundamental groundwater physical equations. The most used and classical methodologies, such as Finite Difference (FD) and Finite Element (FE) Methods, use iterative solvers which are associated with high computational cost. This study proposes a physics-based convolutional encoder-decoder neural network as a surrogate model to quickly calculate the response of the groundwater system. Holding strong promise in cross-domain mappings, encoder-decoder networks are applicable for learning complex input-output mappings of physical systems. This manuscript presents an Attention U-Net model that attempts to capture the fundamental input-output relations of the groundwater system and generates solutions of hydraulic head in the whole domain given a set of physical parameters and boundary conditions. The model accurately predicts the steady state response of a highly heterogeneous groundwater system given the locations and piezometric head of up to 3 wells as input. The network learns to pay attention only in the relevant parts of the domain and the generated hydraulic head field corresponds to the target samples in great detail. Even relative to coarse finite difference approximations the proposed model is shown to be significantly faster than a comparative state-of-the-art numerical solver, thus providing a base for further development of the presented networks as surrogate models for groundwater prediction.

MeshingNet: A New Mesh Generation Method based on Deep Learning

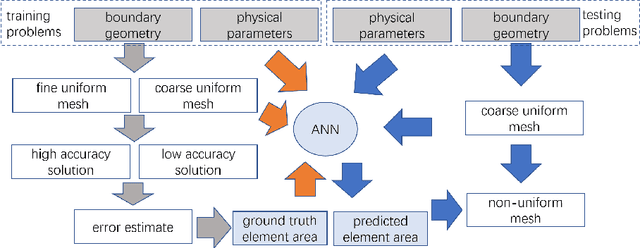
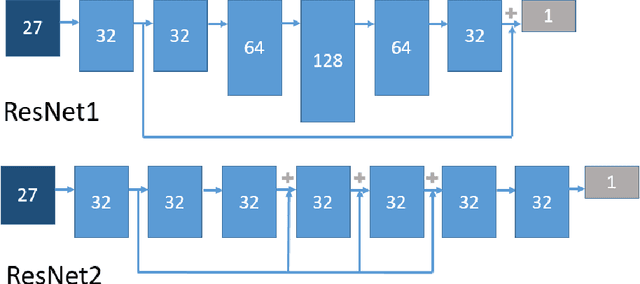
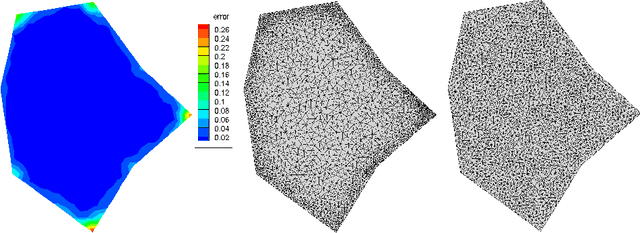
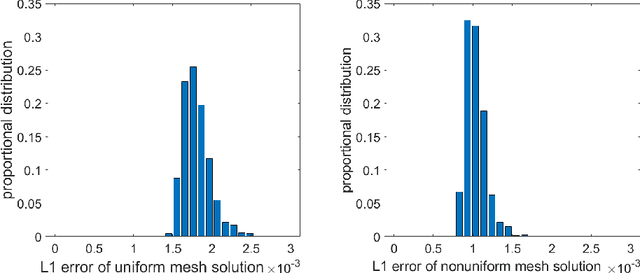
We introduce a novel approach to automatic unstructured mesh generation using machine learning to predict an optimal finite element mesh for a previously unseen problem. The framework that we have developed is based around training an artificial neural network (ANN) to guide standard mesh generation software, based upon a prediction of the required local mesh density throughout the domain. We describe the training regime that is proposed, based upon the use of \emph{a posteriori} error estimation, and discuss the topologies of the ANNs that we have considered. We then illustrate performance using two standard test problems, a single elliptic partial differential equation (PDE) and a system of PDEs associated with linear elasticity. We demonstrate the effective generation of high quality meshes for arbitrary polygonal geometries and a range of material parameters, using a variety of user-selected error norms.