Mixing It Up: The Cocktail Effect of Multi-Task Fine-Tuning on LLM Performance -- A Case Study in Finance

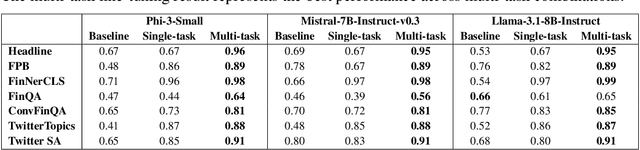
The application of large language models (LLMs) in domain-specific contexts, including finance, has expanded rapidly. Domain-specific LLMs are typically evaluated based on their performance in various downstream tasks relevant to the domain. In this work, we present a detailed analysis of fine-tuning LLMs for such tasks. Somewhat counterintuitively, we find that in domain-specific cases, fine-tuning exclusively on the target task is not always the most effective strategy. Instead, multi-task fine-tuning - where models are trained on a cocktail of related tasks - can significantly enhance performance. We demonstrate how this approach enables a small model, such as Phi-3-Mini, to achieve state-of-the-art results, even surpassing the much larger GPT-4-o model on financial benchmarks. Our study involves a large-scale experiment, training over 200 models using several widely adopted LLMs as baselines, and empirically confirms the benefits of multi-task fine-tuning. Additionally, we explore the use of general instruction data as a form of regularization, suggesting that it helps minimize performance degradation. We also investigate the inclusion of mathematical data, finding improvements in numerical reasoning that transfer effectively to financial tasks. Finally, we note that while fine-tuning for downstream tasks leads to targeted improvements in task performance, it does not necessarily result in broader gains in domain knowledge or complex domain reasoning abilities.

Fine-Tuning or Retrieval? Comparing Knowledge Injection in LLMs

Large language models (LLMs) encapsulate a vast amount of factual information within their pre-trained weights, as evidenced by their ability to answer diverse questions across different domains. However, this knowledge is inherently limited, relying heavily on the characteristics of the training data. Consequently, using external datasets to incorporate new information or refine the capabilities of LLMs on previously seen information poses a significant challenge. In this study, we compare two common approaches: fine-tuning and retrieval-augmented generation (RAG). We evaluate both approaches on a variety of knowledge-intensive tasks across different topics. Our findings reveal that while fine-tuning offers some improvement, RAG consistently outperforms it, both for existing knowledge encountered during training and entirely new knowledge. Moreover, we find that LLMs struggle to learn new factual information through fine-tuning, and that exposing them to numerous variations of the same fact during training could alleviate this problem.

DiTTO: Diffusion-inspired Temporal Transformer Operator

Solving partial differential equations (PDEs) using a data-driven approach has become increasingly common. The recent development of the operator learning paradigm has enabled the solution of a broader range of PDE-related problems. We propose an operator learning method to solve time-dependent PDEs continuously in time without needing any temporal discretization. The proposed approach, named DiTTO, is inspired by latent diffusion models. While diffusion models are usually used in generative artificial intelligence tasks, their time-conditioning mechanism is extremely useful for PDEs. The diffusion-inspired framework is combined with elements from the Transformer architecture to improve its capabilities. We demonstrate the effectiveness of the new approach on a wide variety of PDEs in multiple dimensions, namely the 1-D Burgers' equation, 2-D Navier-Stokes equations, and the acoustic wave equation in 2-D and 3-D. DiTTO achieves state-of-the-art results in terms of accuracy for these problems. We also present a method to improve the performance of DiTTO by using fast sampling concepts from diffusion models. Finally, we show that DiTTO can accurately perform zero-shot super-resolution in time.

Understanding the Efficacy of U-Net & Vision Transformer for Groundwater Numerical Modelling

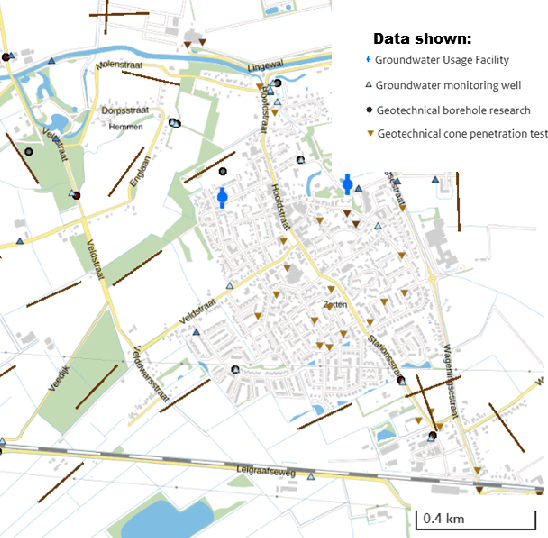
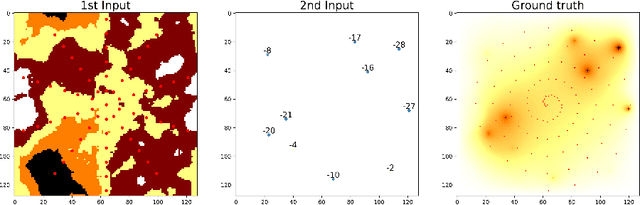
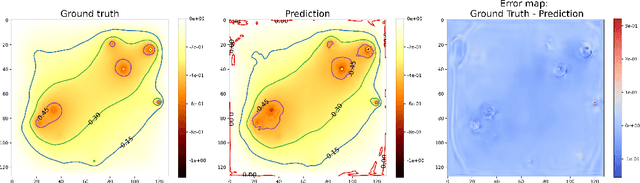
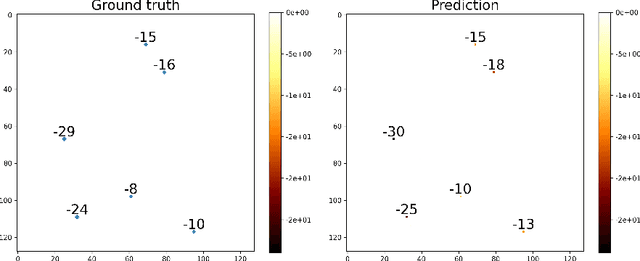
This paper presents a comprehensive comparison of various machine learning models, namely U-Net, U-Net integrated with Vision Transformers (ViT), and Fourier Neural Operator (FNO), for time-dependent forward modelling in groundwater systems. Through testing on synthetic datasets, it is demonstrated that U-Net and U-Net + ViT models outperform FNO in accuracy and efficiency, especially in sparse data scenarios. These findings underscore the potential of U-Net-based models for groundwater modelling in real-world applications where data scarcity is prevalent.

ViTO: Vision Transformer-Operator

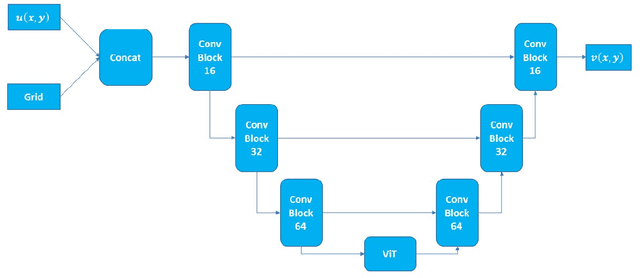
We combine vision transformers with operator learning to solve diverse inverse problems described by partial differential equations (PDEs). Our approach, named ViTO, combines a U-Net based architecture with a vision transformer. We apply ViTO to solve inverse PDE problems of increasing complexity, namely for the wave equation, the Navier-Stokes equations and the Darcy equation. We focus on the more challenging case of super-resolution, where the input dataset for the inverse problem is at a significantly coarser resolution than the output. The results we obtain are comparable or exceed the leading operator network benchmarks in terms of accuracy. Furthermore, ViTO`s architecture has a small number of trainable parameters (less than 10% of the leading competitor), resulting in a performance speed-up of over 5x when averaged over the various test cases.

A Convolutional Dispersion Relation Preserving Scheme for the Acoustic Wave Equation

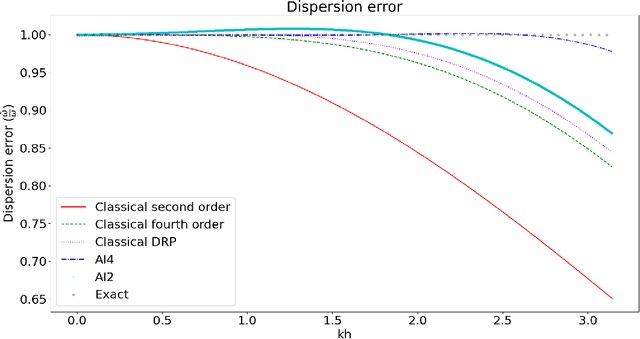
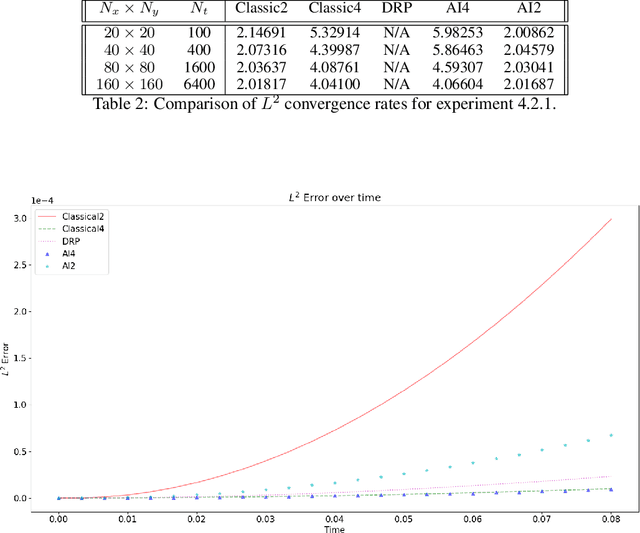
We propose an accurate numerical scheme for approximating the solution of the two dimensional acoustic wave problem. We use machine learning to find a stencil suitable even in the presence of high wavenumbers. The proposed scheme incorporates physically informed elements from the field of optimized numerical schemes into a convolutional optimization machine learning algorithm.