Large scale scattering using fast solvers based on neural operators

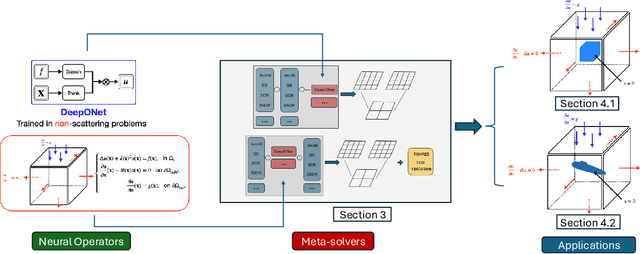
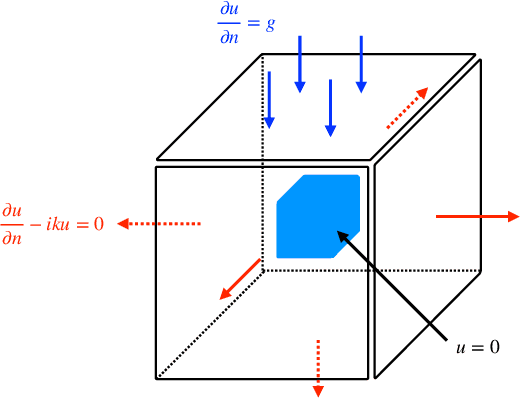
We extend a recently proposed machine-learning-based iterative solver, i.e. the hybrid iterative transferable solver (HINTS), to solve the scattering problem described by the Helmholtz equation in an exterior domain with a complex absorbing boundary condition. The HINTS method combines neural operators (NOs) with standard iterative solvers, e.g. Jacobi and Gauss-Seidel (GS), to achieve better performance by leveraging the spectral bias of neural networks. In HINTS, some iterations of the conventional iterative method are replaced by inferences of the pre-trained NO. In this work, we employ HINTS to solve the scattering problem for both 2D and 3D problems, where the standard iterative solver fails. We consider square and triangular scatterers of various sizes in 2D, and a cube and a model submarine in 3D. We explore and illustrate the extrapolation capability of HINTS in handling diverse geometries of the scatterer, which is achieved by training the NO on non-scattering scenarios and then deploying it in HINTS to solve scattering problems. The accurate results demonstrate that the NO in HINTS method remains effective without retraining or fine-tuning it whenever a new scatterer is given. Taken together, our results highlight the adaptability and versatility of the extended HINTS methodology in addressing diverse scattering problems.

DiTTO: Diffusion-inspired Temporal Transformer Operator

Solving partial differential equations (PDEs) using a data-driven approach has become increasingly common. The recent development of the operator learning paradigm has enabled the solution of a broader range of PDE-related problems. We propose an operator learning method to solve time-dependent PDEs continuously in time without needing any temporal discretization. The proposed approach, named DiTTO, is inspired by latent diffusion models. While diffusion models are usually used in generative artificial intelligence tasks, their time-conditioning mechanism is extremely useful for PDEs. The diffusion-inspired framework is combined with elements from the Transformer architecture to improve its capabilities. We demonstrate the effectiveness of the new approach on a wide variety of PDEs in multiple dimensions, namely the 1-D Burgers' equation, 2-D Navier-Stokes equations, and the acoustic wave equation in 2-D and 3-D. DiTTO achieves state-of-the-art results in terms of accuracy for these problems. We also present a method to improve the performance of DiTTO by using fast sampling concepts from diffusion models. Finally, we show that DiTTO can accurately perform zero-shot super-resolution in time.

ViTO: Vision Transformer-Operator

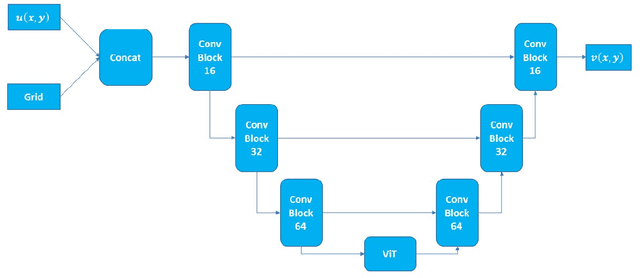
We combine vision transformers with operator learning to solve diverse inverse problems described by partial differential equations (PDEs). Our approach, named ViTO, combines a U-Net based architecture with a vision transformer. We apply ViTO to solve inverse PDE problems of increasing complexity, namely for the wave equation, the Navier-Stokes equations and the Darcy equation. We focus on the more challenging case of super-resolution, where the input dataset for the inverse problem is at a significantly coarser resolution than the output. The results we obtain are comparable or exceed the leading operator network benchmarks in terms of accuracy. Furthermore, ViTO`s architecture has a small number of trainable parameters (less than 10% of the leading competitor), resulting in a performance speed-up of over 5x when averaged over the various test cases.

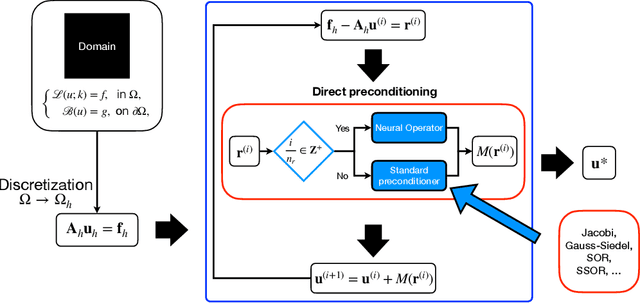
A Hybrid Iterative Numerical Transferable Solver (HINTS) for PDEs Based on Deep Operator Network and Relaxation Methods

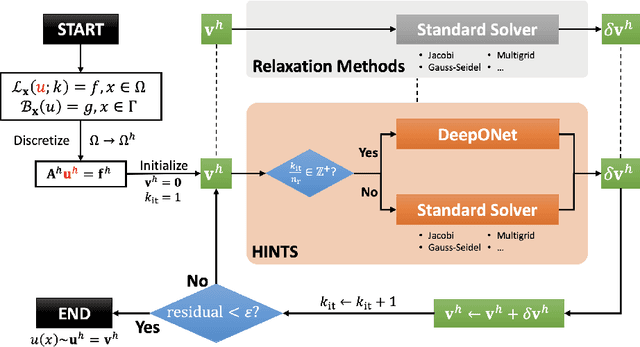
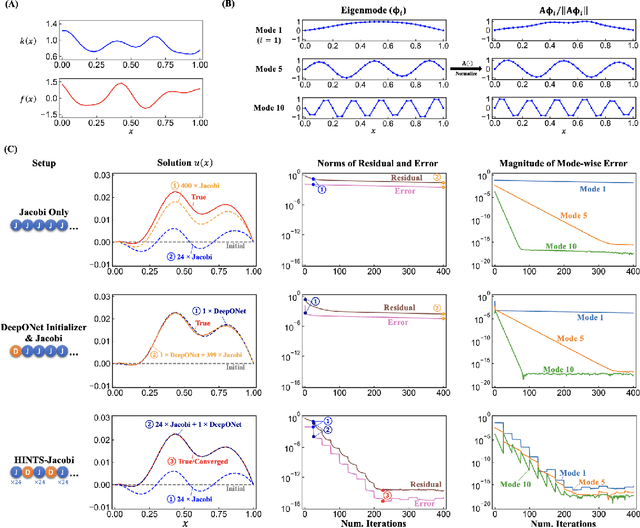
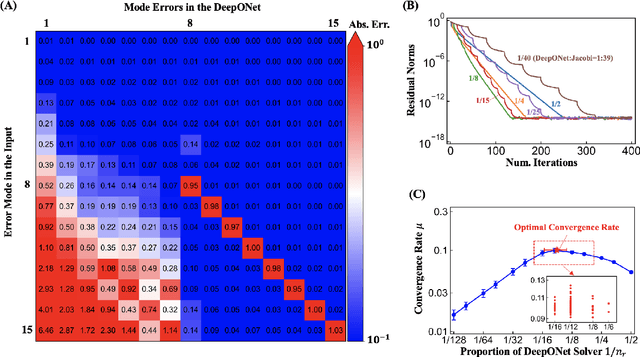
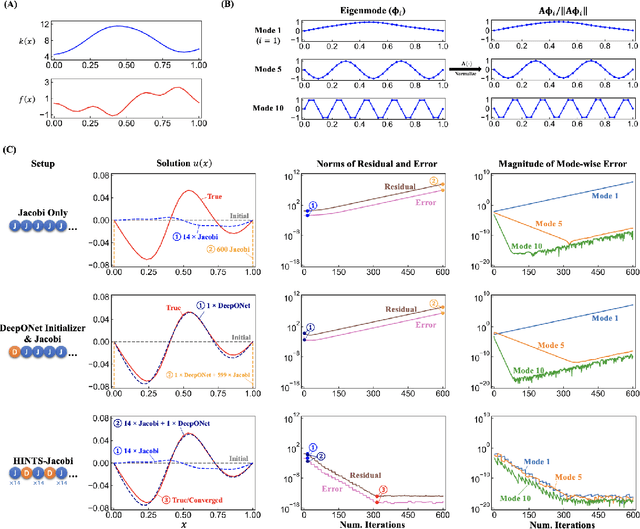
Iterative solvers of linear systems are a key component for the numerical solutions of partial differential equations (PDEs). While there have been intensive studies through past decades on classical methods such as Jacobi, Gauss-Seidel, conjugate gradient, multigrid methods and their more advanced variants, there is still a pressing need to develop faster, more robust and reliable solvers. Based on recent advances in scientific deep learning for operator regression, we propose HINTS, a hybrid, iterative, numerical, and transferable solver for differential equations. HINTS combines standard relaxation methods and the Deep Operator Network (DeepONet). Compared to standard numerical solvers, HINTS is capable of providing faster solutions for a wide class of differential equations, while preserving the accuracy close to machine zero. Through an eigenmode analysis, we find that the individual solvers in HINTS target distinct regions in the spectrum of eigenmodes, resulting in a uniform convergence rate and hence exceptional performance of the hybrid solver overall. Moreover, HINTS applies to equations in multidimensions, and is flexible with regards to computational domain and transferable to different discretizations.

A physically-informed Deep-Learning approach for locating sources in a waveguide

Inverse source problems are central to many applications in acoustics, geophysics, non-destructive testing, and more. Traditional imaging methods suffer from the resolution limit, preventing distinction of sources separated by less than the emitted wavelength. In this work we propose a method based on physically-informed neural-networks for solving the source refocusing problem, constructing a novel loss term which promotes super-resolving capabilities of the network and is based on the physics of wave propagation. We demonstrate the approach in the setup of imaging an a-priori unknown number of point sources in a two-dimensional rectangular waveguide from measurements of wavefield recordings along a vertical cross-section. The results show the ability of the method to approximate the locations of sources with high accuracy, even when placed close to each other.

A Convolutional Dispersion Relation Preserving Scheme for the Acoustic Wave Equation

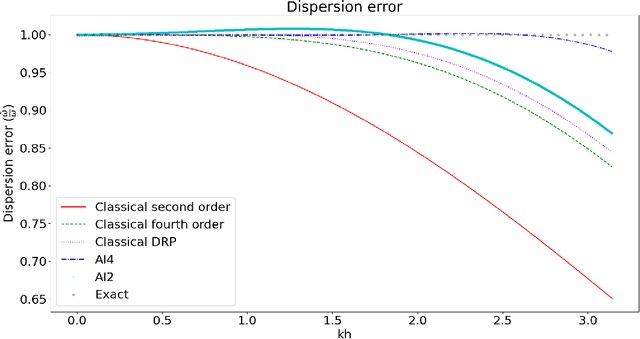
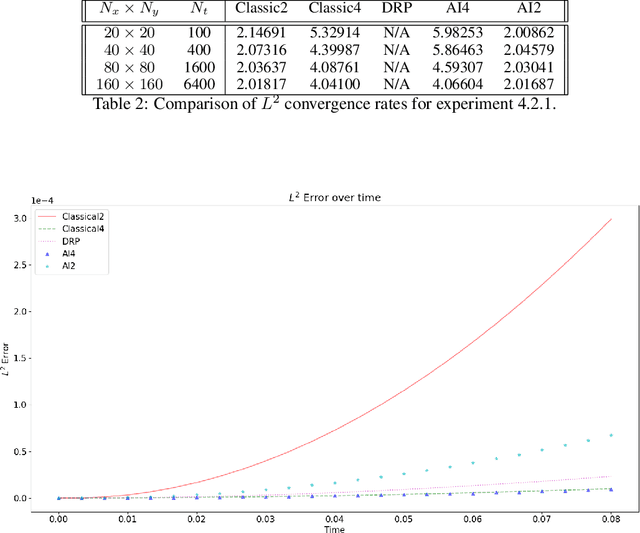
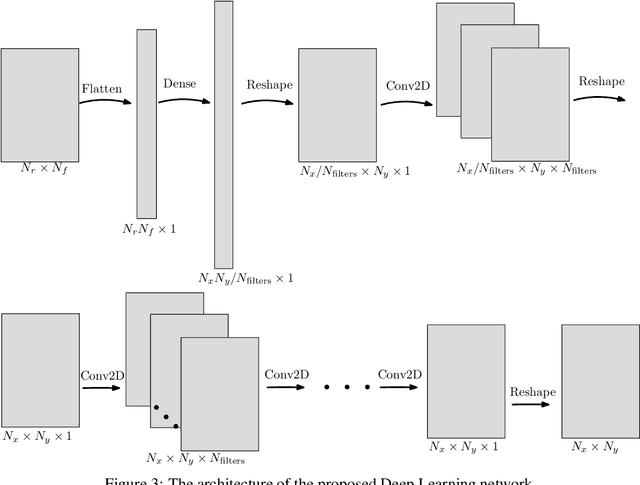
We propose an accurate numerical scheme for approximating the solution of the two dimensional acoustic wave problem. We use machine learning to find a stencil suitable even in the presence of high wavenumbers. The proposed scheme incorporates physically informed elements from the field of optimized numerical schemes into a convolutional optimization machine learning algorithm.